In this paper we give a tutorial on how quantum mechanics can be used to improve computation. Our challenge: solving an exponentially difficult problem for a conventional computer---that of factoring a large number. As a prelude, we review the standard tools of computation, universal gates and machines. These ideas are then applied first to classical, dissipationless computers and then to quantum computers. A schematic model of a quantum computer is described as well as some of the subtleties in its programming. The Shor algorithm [1,2] for efficiently factoring numbers on a quantum computer is presented in two parts: the quantum procedure within the algorithm and the classical algorithm that calls the quantum procedure. The mathematical structure in factoring which makes the Shor algorithm possible is discussed. We conclude with an outlook to the feasibility and prospects for quantum computation in the coming years.
Let us start by describing the problem at hand: factoring
a number N into its prime factors (e.g., the number 51688
may be decomposed as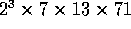 
).
A convenient way to quantify how quickly a particular algorithm may solve
a problem is to ask how the number of steps to complete the algorithm scales
with the size of the ``input'' the algorithm is fed. For the factoring
problem, this input is just the number N we wish to factor; hence
the length of the input is 
.
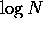(The base of the logarithm is determined by our numbering system. Thus
a base of
2 gives the length in binary; a base of 10 in decimal.)
`Reasonable' algorithms are ones which scale as some small-degree polynomial
in the input size (with a degree of perhaps 2 or 3).
On conventional computers the best known factoring algorithm
runs in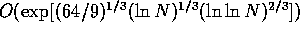 
steps [3].
This algorithm, therefore, scales exponentially with the input size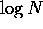
.
For instance, in 1994 a 129 digit number (known as RSA129 [3'])
was successfully factored using this algorithm on approximately 1600 workstations
scattered around the world; the entire factorization took eight months
[4].
Using this to estimate the prefactor of the above exponential scaling,
we find that it would take roughly 800,000 years to factor a 250 digit
number with the same computer power; similarly, a 1000 digit number would
require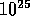 
years (significantly
lon ger than the age of the universe). The difficulty of factoring large
numbers is crucial for public-key cryptosystems, such as ones used by banks.
There, such codes rely on the difficulty of factoring numbers with around
250 digits.
Recently, an algorithm was developed for factoring numbers
on a quantum computer which runs in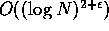 
steps where
is small [1].
This is roughly quadratic in the input size, so factoring a 1000
digit number with such an algorithm would require only a few million steps.
The implication is that public key cryptosystems based on factoring may
be breakable.
To give you an idea of how this exponential improvement
might be possible, we review an elementary quantum mechanical experiment
that demonstrates where such power may lie hidden [5].
The two-slit experiment is prototypic for observing quantum mechanical
behavior: A source emits photons, electrons or other particles that arrive
at a pair of slits. These particles undergo unitary evolution and finally
measurement. We see an interference pattern, with both slits open, which
wholely vanishes if either slit is covered. In some sense, the particles
pass through both slits in parallel. If such unitary evolution were to
represent a calculation (or an operation within a calculation) then the
quantum system would be performing computations in parallel. Quantum parallelism
comes for free. The output of this system would be given by the constructive
interference among the parallel computations.