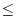 f(x1,
... , xn) + f(y1, ... , yn)
f(x1,
... , xn) + f(y1, ... , yn)Who of us would not be glad to lift the veil behind which the future lies hidden; to cast a glance at the next advances of our science and at the secrets of its development during future centuries? What particular goals will there be toward which the leading mathematical spirits of coming generations will strive? What new methods and new facts in the wide and rich field of mathematical thought will the new centuries disclose?
History teaches the continuity of the development of science. We know that every age has its own problems, which the following age either solves or casts aside as profitless and replaces by new ones. If we would obtain an idea of the probable development of mathematical knowledge in the immediate future, we must let the unsettled questions pass before our minds and look over the problems which the science of today sets and whose solution we expect from the future. To such a review of problems the present day, lying at the meeting of the centuries, seems to me well adapted. For the close of a great epoch not only invites us to look back into the past but also directs our thoughts to the unknown future.
The deep significance of certain problems for the advance of mathematical science in general and the important role which they play in the work of the individual investigator are not to be denied. As long as a branch of science offers an abundance of problems, so long is it alive; a lack of problems foreshadows extinction or the cessation of independent development. Just as every human undertaking pursues certain objects, so also mathematical research requires its problems. It is by the solution of problems that the investigator tests the temper of his steel; he finds new methods and new outlooks, and gains a wider and freer horizon.
It is difficult and often impossible to judge the value of a problem correctly in advance; for the final award depends upon the gain which science obtains from the problem. Nevertheless we can ask whether there are general criteria which mark a good mathematical problem. An old French mathematician said: "A mathematical theory is not to be considered complete until you have made it so clear that you can explain it to the first man whom you meet on the street." This clearness and ease of comprehension, here insisted on for a mathematical theory, I should still more demand for a mathematical problem if it is to be perfect; for what is clear and easily comprehended attracts, the complicated repels us.
Moreover a mathematical problem should be difficult in order to entice us, yet not completely inaccessible, lest it mock at our efforts. It should be to us a guide post on the mazy paths to hidden truths, and ultimately a reminder of our pleasure in the successful solution.
The mathematicians of past centuries were accustomed to devote themselves to the solution of difficult particular problems with passionate zeal. They knew the value of difficult problems. I remind you only of the "problem of the line of quickest descent," proposed by John Bernoulli. Experience teaches, explains Bernoulli in the public announcement of this problem, that lofty minds are led to strive for the advance of science by nothing more than by laying before them difficult and at the same time useful problems, and he therefore hopes to earn the thanks of the mathematical world by following the example of men like Mersenne, Pascal, Fermat, Viviani and others and laying before the distinguished analysts of his time a problem by which, as a touchstone, they may test the value of their methods and measure their strength. The calculus of variations owes its origin to this problem of Bernoulli and to similar problems.
Fermat had asserted, as is well known, that the diophantine equation
(x, y and z integers) is unsolvable--except in certain self evident cases. The attempt to prove this impossibility offers a striking example of the inspiring effect which such a very special and apparently unimportant problem may have upon science. For Kummer, incited by Fermat's problem, was led to the introduction of ideal numbers and to the discovery of the law of the unique decomposition of the numbers of a circular field into ideal prime factors--a law which today, in its generalization to any algebraic field by Dedekind and Kronecker, stands at the center of the modern theory of numbers and whose significance extends far beyond the boundaries of number theory into the realm of algebra and the theory of functions.
To speak of a very different region of research, I remind you of the problem of three bodies. The fruitful methods and the far-reaching principles which Poincaré has brought into celestial mechanics and which are today recognized and applied in practical astronomy are due to the circumstance that he undertook to treat anew that difficult problem and to approach nearer a solution.
The two last mentioned problems--that of Fermat and the problem of the three bodies--seem to us almost like opposite poles--the former a free invention of pure reason, belonging to the region of abstract number theory, the latter forced upon us by astronomy and necessary to an understanding of the simplest fundamental phenomena of nature.
But it often happens also that the same special problem finds application in the most unlike branches of mathematical knowledge. So, for example, the problem of the shortest line plays a chief and historically important part in the foundations of geometry, in the theory of curved lines and surfaces, in mechanics and in the calculus of variations. And how convincingly has F. Klein, in his work on the icosahedron, pictured the significance which attaches to the problem of the regular polyhedra in elementary geometry, in group theory, in the theory of equations and in that of linear differential equations.
In order to throw light on the importance of certain problems, I may also refer to Weierstrass, who spoke of it as his happy fortune that he found at the outset of his scientific career a problem so important as Jacobi's problem of inversion on which to work.
Having now recalled to mind the general importance of problems in mathematics, let us turn to the question from what sources this science derives its problems. Surely the first and oldest problems in every branch of mathematics spring from experience and are suggested by the world of external phenomena. Even the rules of calculation with integers must have been discovered in this fashion in a lower stage of human civilization, just as the child of today learns the application of these laws by empirical methods. The same is true of the first problems of geometry, the problems bequeathed us by antiquity, such as the duplication of the cube, the squaring of the circle; also the oldest problems in the theory of the solution of numerical equations, in the theory of curves and the differential and integral calculus, in the calculus of variations, the theory of Fourier series and the theory of potential--to say nothing of the further abundance of problems properly belonging to mechanics, astronomy and physics.
But, in the further development of a branch of mathematics, the human mind, encouraged by the success of its solutions, becomes conscious of its independence. It evolves from itself alone, often without appreciable influence from without, by means of logical combination, generalization, specialization, by separating and collecting ideas in fortunate ways, new and fruitful problems, and appears then itself as the real questioner. Thus arose the problem of prime numbers and the other problems of number theory, Galois's theory of equations, the theory of algebraic invariants, the theory of abelian and automorphic functions; indeed almost all the nicer questions of modern arithmetic and function theory arise in this way.
In the meantime, while the creative power of pure reason is at work, the outer world again comes into play, forces upon us new questions from actual experience, opens up new branches of mathematics, and while we seek to conquer these new fields of knowledge for the realm of pure thought, we often find the answers to old unsolved problems and thus at the same time advance most successfully the old theories. And it seems to me that the numerous and surprising analogies and that apparently prearranged harmony which the mathematician so often perceives in the questions, methods and ideas of the various branches of his science, have their origin in this ever-recurring interplay between thought and experience.
It remains to discuss briefly what general requirements may be justly laid down for the solution of a mathematical problem. I should say first of all, this: that it shall be possible to establish the correctness of the solution by means of a finite number of steps based upon a finite number of hypotheses which are implied in the statement of the problem and which must always be exactly formulated. This requirement of logical deduction by means of a finite number of processes is simply the requirement of rigor in reasoning. Indeed the requirement of rigor, which has become proverbial in mathematics, corresponds to a universal philosophical necessity of our understanding; and, on the other hand, only by satisfying this requirement do the thought content and the suggestiveness of the problem attain their full effect. A new problem, especially when it comes from the world of outer experience, is like a young twig, which thrives and bears fruit only when it is grafted carefully and in accordance with strict horticultural rules upon the old stem, the established achievements of our mathematical science.
Besides it is an error to believe that rigor in the proof is the enemy of simplicity. On the contrary we find it confirmed by numerous examples that the rigorous method is at the same time the simpler and the more easily comprehended. The very effort for rigor forces us to find out simpler methods of proof. It also frequently leads the way to methods which are more capable of development than the old methods of less rigor. Thus the theory of algebraic curves experienced a considerable simplification and attained greater unity by means of the more rigorous function-theoretical methods and the consistent introduction of transcendental devices. Further, the proof that the power series permits the application of the four elementary arithmetical operations as well as the term by term differentiation and integration, and the recognition of the utility of the power series depending upon this proof contributed materially to the simplification of all analysis, particularly of the theory of elimination and the theory of differential equations, and also of the existence proofs demanded in those theories. But the most striking example for my statement is the calculus of variations. The treatment of the first and second variations of definite integrals required in part extremely complicated calculations, and the processes applied by the old mathematicians had not the needful rigor. Weierstrass showed us the way to a new and sure foundation of the calculus of variations. By the examples of the simple and double integral I will show briefly, at the close of my lecture, how this way leads at once to a surprising simplification of the calculus of variations. For in the demonstration of the necessary and sufficient criteria for the occurrence of a maximum and minimum, the calculation of the second variation and in part, indeed, the wearisome reasoning connected with the first variation may be completely dispensed with--to say nothing of the advance which is involved in the removal of the restriction to variations for which the differential coefficients of the function vary but slightly.
While insisting on rigor in the proof as a requirement for a perfect solution of a problem, I should like, on the other hand, to oppose the opinion that only the concepts of analysis, or even those of arithmetic alone, are susceptible of a fully rigorous treatment. This opinion, occasionally advocated by eminent men, I consider entirely erroneous. Such a one-sided interpretation of the requirement of rigor would soon lead to the ignoring of all concepts arising from geometry, mechanics and physics, to a stoppage of the flow of new material from the outside world, and finally, indeed, as a last consequence, to the rejection of the ideas of the continuum and of the irrational number. But what an important nerve, vital to mathematical science, would be cut by the extirpation of geometry and mathematical physics! On the contrary I think that wherever, from the side of the theory of knowledge or in geometry, or from the theories of natural or physical science, mathematical ideas come up, the problem arises for mathematical science to investigate the principles underlying these ideas and so to establish them upon a simple and complete system of axioms, that the exactness of the new ideas and their applicability to deduction shall be in no respect inferior to those of the old arithmetical concepts.
To new concepts correspond, necessarily, new signs. These we choose in such a way that they remind us of the phenomena which were the occasion for the formation of the new concepts. So the geometrical figures are signs or mnemonic symbols of space intuition and are used as such by all mathematicians. Who does not always use along with the double inequality a > b > c the picture of three points following one another on a straight line as the geometrical picture of the idea "between"? Who does not make use of drawings of segments and rectangles enclosed in one another, when it is required to prove with perfect rigor a difficult theorem on the continuity of functions or the existence of points of condensation? Who could dispense with the figure of the triangle, the circle with its center, or with the cross of three perpendicular axes? Or who would give up the representation of the vector field, or the picture of a family of curves or surfaces with its envelope which plays so important a part in differential geometry, in the theory of differential equations, in the foundation of the calculus of variations and in other purely mathematical sciences?
The arithmetical symbols are written diagrams and the geometrical figures are graphic formulas; and no mathematician could spare these graphic formulas, any more than in calculation the insertion and removal of parentheses or the use of other analytical signs.
The use of geometrical signs as a means of strict proof presupposes the exact knowledge and complete mastery of the axioms which underlie those figures; and in order that these geometrical figures may be incorporated in the general treasure of mathematical signs, there is necessary a rigorous axiomatic investigation of their conceptual content. Just as in adding two numbers, one must place the digits under each other in the right order, so that only the rules of calculation, i. e., the axioms of arithmetic, determine the correct use of the digits, so the use of geometrical signs is determined by the axioms of geometrical concepts and their combinations.
The agreement between geometrical and arithmetical thought is shown also in that we do not habitually follow the chain of reasoning back to the axioms in arithmetical, any more than in geometrical discussions. On the contrary we apply, especially in first attacking a problem, a rapid, unconscious, not absolutely sure combination, trusting to a certain arithmetical feeling for the behavior of the arithmetical symbols, which we could dispense with as little in arithmetic as with the geometrical imagination in geometry. As an example of an arithmetical theory operating rigorously with geometrical ideas and signs, I may mention Minkowski's work, Die Geometrie der Zahlen.2
Some remarks upon the difficulties which mathematical problems may offer, and the means of surmounting them, may be in place here.
If we do not succeed in solving a mathematical problem, the reason frequently consists in our failure to recognize the more general standpoint from which the problem before us appears only as a single link in a chain of related problems. After finding this standpoint, not only is this problem frequently more accessible to our investigation, but at the same time we come into possession of a method which is applicable also to related problems. The introduction of complex paths of integration by Cauchy and of the notion of the IDEALS in number theory by Kummer may serve as examples. This way for finding general methods is certainly the most practicable and the most certain; for he who seeks for methods without having a definite problem in mind seeks for the most part in vain.
In dealing with mathematical problems, specialization plays, as I believe, a still more important part than generalization. Perhaps in most cases where we seek in vain the answer to a question, the cause of the failure lies in the fact that problems simpler and easier than the one in hand have been either not at all or incompletely solved. All depends, then, on finding out these easier problems, and on solving them by means of devices as perfect as possible and of concepts capable of generalization. This rule is one of the most important levers for overcoming mathematical difficulties and it seems to me that it is used almost always, though perhaps unconsciously.
Occasionally it happens that we seek the solution under insufficient hypotheses or in an incorrect sense, and for this reason do not succeed. The problem then arises: to show the impossibility of the solution under the given hypotheses, or in the sense contemplated. Such proofs of impossibility were effected by the ancients, for instance when they showed that the ratio of the hypotenuse to the side of an isosceles right triangle is irrational. In later mathematics, the question as to the impossibility of certain solutions plays a preeminent part, and we perceive in this way that old and difficult problems, such as the proof of the axiom of parallels, the squaring of the circle, or the solution of equations of the fifth degree by radicals have finally found fully satisfactory and rigorous solutions, although in another sense than that originally intended. It is probably this important fact along with other philosophical reasons that gives rise to the conviction (which every mathematician shares, but which no one has as yet supported by a proof) that every definite mathematical problem must necessarily be susceptible of an exact settlement, either in the form of an actual answer to the question asked, or by the proof of the impossibility of its solution and therewith the necessary failure of all attempts. Take any definite unsolved problem, such as the question as to the irrationality of the Euler-Mascheroni constant C, or the existence of an infinite number of prime numbers of the form 2n + 1. However unapproachable these problems may seem to us and however helpless we stand before them, we have, nevertheless, the firm conviction that their solution must follow by a finite number of purely logical processes.
Is this axiom of the solvability of every problem a peculiarity characteristic of mathematical thought alone, or is it possibly a general law inherent in the nature of the mind, that all questions which it asks must be answerable? For in other sciences also one meets old problems which have been settled in a manner most satisfactory and most useful to science by the proof of their impossibility. I instance the problem of perpetual motion. After seeking in vain for the construction of a perpetual motion machine, the relations were investigated which must subsist between the forces of nature if such a machine is to be impossible;3 and this inverted question led to the discovery of the law of the conservation of energy, which, again, explained the impossibility of perpetual motion in the sense originally intended.
This conviction of the solvability of every mathematical problem is a powerful incentive to the worker. We hear within us the perpetual call: There is the problem. Seek its solution. You can find it by pure reason, for in mathematics there is no ignorabimus.
The supply of problems in mathematics is inexhaustible, and as soon as one problem is solved numerous others come forth in its place. Permit me in the following, tentatively as it were, to mention particular definite problems, drawn from various branches of mathematics, from the discussion of which an advancement of science may be expected.
Let us look at the principles of analysis and geometry. The most suggestive and notable achievements of the last century in this field are, as it seems to me, the arithmetical formulation of the concept of the continuum in the works of Cauchy, Bolzano and Cantor, and the discovery of non-euclidean geometry by Gauss, Bolyai, and Lobachevsky. I therefore first direct your attention to some problems belonging to these fields.
Every system of infinitely many real numbers, i. e., every assemblage of numbers (or points), is either equivalent to the assemblage of natural integers, 1, 2, 3,... or to the assemblage of all real numbers and therefore to the continuum, that is, to the points of a line; as regards equivalence there are, therefore, only two assemblages of numbers, the countable assemblage and the continuum.
From this theorem it would follow at once that the continuum has the next cardinal number beyond that of the countable assemblage; the proof of this theorem would, therefore, form a new bridge between the countable assemblage and the continuum.
Let me mention another very remarkable statement of Cantor's which stands in the closest connection with the theorem mentioned and which, perhaps, offers the key to its proof. Any system of real numbers is said to be ordered, if for every two numbers of the system it is determined which one is the earlier and which the later, and if at the same time this determination is of such a kind that, if a is before b and b is before c, then a always comes before c. The natural arrangement of numbers of a system is defined to be that in which the smaller precedes the larger. But there are, as is easily seen infinitely many other ways in which the numbers of a system may be arranged.
If we think of a definite arrangement of numbers and select from them a particular system of these numbers, a so-called partial system or assemblage, this partial system will also prove to be ordered. Now Cantor considers a particular kind of ordered assemblage which he designates as a well ordered assemblage and which is characterized in this way, that not only in the assemblage itself but also in every partial assemblage there exists a first number. The system of integers 1, 2, 3, ... in their natural order is evidently a well ordered assemblage. On the other hand the system of all real numbers, i. e., the continuum in its natural order, is evidently not well ordered. For, if we think of the points of a segment of a straight line, with its initial point excluded, as our partial assemblage, it will have no first element.
The question now arises whether the totality
of all numbers may not be arranged in another manner so that every partial
assemblage may have a first element, i. e., whether the continuum
cannot be considered as a well ordered assemblage--a question which Cantor
thinks must be answered in the affirmative. It appears to me most desirable
to obtain a direct proof of this remarkable statement of Cantor's, perhaps
by actually giving an arrangement of numbers such that in every partial
system a first number can be pointed out.
But above all I wish to designate the following as the most important among the numerous questions which can be asked with regard to the axioms: To prove that they are not contradictory, that is, that a definite number of logical steps based upon them can never lead to contradictory results.
In geometry, the proof of the compatibility of the axioms can be effected by constructing a suitable field of numbers, such that analogous relations between the numbers of this field correspond to the geometrical axioms. Any contradiction in the deductions from the geometrical axioms must thereupon be recognizable in the arithmetic of this field of numbers. In this way the desired proof for the compatibility of the geometrical axioms is made to depend upon the theorem of the compatibility of the arithmetical axioms.
On the other hand a direct method is needed for the proof of the compatibility of the arithmetical axioms. The axioms of arithmetic are essentially nothing else than the known rules of calculation, with the addition of the axiom of continuity. I recently collected them4 and in so doing replaced the axiom of continuity by two simpler axioms, namely, the well-known axiom of Archimedes, and a new axiom essentially as follows: that numbers form a system of things which is capable of no further extension, as long as all the other axioms hold (axiom of completeness). I am convinced that it must be possible to find a direct proof for the compatibility of the arithmetical axioms, by means of a careful study and suitable modification of the known methods of reasoning in the theory of irrational numbers.
To show the significance of the problem from another point of view, I add the following observation: If contradictory attributes be assigned to a concept, I say, that mathematically the concept does not exist. So, for example, a real number whose square is -l does not exist mathematically. But if it can be proved that the attributes assigned to the concept can never lead to a contradiction by the application of a finite number of logical processes, I say that the mathematical existence of the concept (for example, of a number or a function which satisfies certain conditions) is thereby proved. In the case before us, where we are concerned with the axioms of real numbers in arithmetic, the proof of the compatibility of the axioms is at the same time the proof of the mathematical existence of the complete system of real numbers or of the continuum. Indeed, when the proof for the compatibility of the axioms shall be fully accomplished, the doubts which have been expressed occasionally as to the existence of the complete system of real numbers will become totally groundless. The totality of real numbers, i. e., the continuum according to the point of view just indicated, is not the totality of all possible series in decimal fractions, or of all possible laws according to which the elements of a fundamental sequence may proceed. It is rather a system of things whose mutual relations are governed by the axioms set up and for which all propositions, and only those, are true which can be derived from the axioms by a finite number of logical processes. In my opinion, the concept of the continuum is strictly logically tenable in this sense only. It seems to me, indeed, that this corresponds best also to what experience and intuition tell us. The concept of the continuum or even that of the system of all functions exists, then, in exactly the same sense as the system of integral, rational numbers, for example, or as Cantor's higher classes of numbers and cardinal numbers. For I am convinced that the existence of the latter, just as that of the continuum, can be proved in the sense I have described; unlike the system of all cardinal numbers or of all Cantor s alephs, for which, as may be shown, a system of axioms, compatible in my sense, cannot be set up. Either of these systems is, therefore, according to my terminology, mathematically non-existent.
From the field of the foundations of geometry
I should like to mention the following problem:
One finds that such a geometry really exists
and is no other than that which Minkowski constructed in his book, Geometrie
der Zahlen,8
and made the basis of his arithmetical investigations. Minkowski's is therefore
also a geometry standing next to the ordinary euclidean geometry; it is
essentially characterized by the following stipulations:
1. The points which are at equal distances from a fixed point O
lie on a convex closed surface of the ordinary euclidean space with O
as a center.
2. Two segments are said to be equal when one can be carried into the
other by a translation of the ordinary euclidean space.
In Minkowski's geometry the axiom of parallels
also holds. By studying the theorem of the straight line as the shortest
distance between two points, I arrived9
at a geometry in which the parallel axiom does not hold, while all other
axioms of Minkowski's geometry are satisfied. The theorem of the straight
line as the shortest distance between two points and the essentially equivalent
theorem of Euclid about the sides of a triangle, play an important part
not only in number theory but also in the theory of surfaces and in the
calculus of variations. For this reason, and because I believe that the
thorough investigation of the conditions for the validity of this theorem
will throw a new light upon the idea of distance, as well as upon other
elementary ideas, e. g., upon the idea of the plane, and the possibility
of its definition by means of the idea of the straight line, the construction
and systematic treatment of the geometries here possible seem to me desirable.
Lie defines a finite continuous group of transformations as a system of transformations
having the property that any two arbitrarily chosen transformations of the system, as
applied successively result in a transformation which also belongs to the system, and which is therefore expressible in the form
where c1, ... , cr are certain functions of a1, ... , ar and b1, ... , br. The group property thus finds its full expression in a system of functional equations and of itself imposes no additional restrictions upon the functions f1, ... , fn; c1, ... , cr. Yet Lie's further treatment of these functional equations, viz., the derivation of the well-known fundamental differential equations, assumes necessarily the continuity and differentiability of the functions defining the group.
As regards continuity: this postulate will certainly be retained for the present--if only with a view to the geometrical and arithmetical applications, in which the continuity of the functions in question appears as a consequence of the axiom of continuity. On the other hand the differentiability of the functions defining the group contains a postulate which, in the geometrical axioms, can be expressed only in a rather forced and complicated manner. Hence there arises the question whether, through the introduction of suitable new variables and parameters, the group can always be transformed into one whose defining functions are differentiable; or whether, at least with the help of certain simple assumptions, a transformation is possible into groups admitting Lie's methods. A reduction to analytic groups is, according to a theorem announced by Lie10 but first proved by Schur,11 always possible when the group is transitive and the existence of the first and certain second derivatives of the functions defining the group is assumed.
For infinite groups the investigation of the corresponding question is, I believe, also of interest. Moreover we are thus led to the wide and interesting field of functional equations which have been heretofore investigated usually only under the assumption of the differentiability of the functions involved. In particular the functional equations treated by Abel12 with so much ingenuity, the difference equations, and other equations occurring in the literature of mathematics, do not directly involve anything which necessitates the requirement of the differentiability of the accompanying functions. In the search for certain existence proofs in the calculus of variations I came directly upon the problem: To prove the differentiability of the function under consideration from the existence of a difference equation. In all these cases, then, the problem arises: In how far are the assertions which we can make in the case of differentiable functions true under proper modifications without this assumption?
It may be further remarked that H. Minkowski in his above-mentioned Geometrie der Zahlen starts with the functional equation
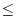 f(x1,
... , xn) + f(y1, ... , yn)
f(x1,
... , xn) + f(y1, ... , yn)and from this actually succeeds in proving the existence of certain differential quotients for the function in question.
On the other hand I wish to emphasize the fact
that there certainly exist analytical functional equations whose sole solutions
are non-differentiable functions. For example a uniform continuous non-differentiable
function 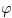 (x) can be constructed
which represents the only solution of the two functional equations
(x) can be constructed
which represents the only solution of the two functional equations
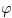 (x +
(x + 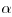 )
-
)
- 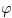 (x) = f(x),
(x) = f(x),
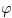 (x +
(x + 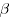 )
-
)
- 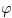 (x) = 0
(x) = 0where 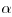 and
and 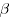 are two real numbers, and f(x) denotes, for all the real
values of x, a regular analytic uniform function. Such functions
are obtained in the simplest manner by means of trigonometrical series
by a process similar to that used by Borel (according to a recent announcement
of Picard)13
for the construction of a doubly periodic, non-analytic solution of a certain
analytic partial differential equation.
are two real numbers, and f(x) denotes, for all the real
values of x, a regular analytic uniform function. Such functions
are obtained in the simplest manner by means of trigonometrical series
by a process similar to that used by Borel (according to a recent announcement
of Picard)13
for the construction of a doubly periodic, non-analytic solution of a certain
analytic partial differential equation.
As to the axioms of the theory of probabilities,14 it seems to me desirable that their logical investigation should be accompanied by a rigorous and satisfactory development of the method of mean values in mathematical physics, and in particular in the kinetic theory of gases.
Important investigations by physicists on the foundations of mechanics are at hand; I refer to the writings of Mach,15 Hertz,16 Boltzmann17 and Volkmann. 18 It is therefore very desirable that the discussion of the foundations of mechanics be taken up by mathematicians also. Thus Boltzmann's work on the principles of mechanics suggests the problem of developing mathematically the limiting processes, there merely indicated, which lead from the atomistic view to the laws of motion of continua. Conversely one might try to derive the laws of the motion of rigid bodies by a limiting process from a system of axioms depending upon the idea of continuously varying conditions of a material filling all space continuously, these conditions being defined by parameters. For the question as to the equivalence of different systems of axioms is always of great theoretical interest.
If geometry is to serve as a model for the treatment of physical axioms, we shall try first by a small number of axioms to include as large a class as possible of physical phenomena, and then by adjoining new axioms to arrive gradually at the more special theories. At the same time Lie's a principle of subdivision can perhaps be derived from profound theory of infinite transformation groups. The mathematician will have also to take account not only of those theories coming near to reality, but also, as in geometry, of all logically possible theories. He must be always alert to obtain a complete survey of all conclusions derivable from the system of axioms assumed.
Further, the mathematician has the duty to test
exactly in each instance whether the new axioms are compatible with the
previous ones. The physicist, as his theories develop, often finds himself
forced by the results of his experiments to make new hypotheses, while
he depends, with respect to the compatibility of the new hypotheses with
the old axioms, solely upon these experiments or upon a certain physical
intuition, a practice which in the rigorously logical building up of a
theory is not admissible. The desired proof of the compatibility of all
assumptions seems to me also of importance, because the effort to obtain
such proof always forces us most effectually to an exact formulation of
the axioms.
If, in an isosceles triangle, the ratio of
the base angle to the angle at the vertex be algebraic but not rational,
the ratio between base and side is always transcendental.
In spite of the simplicity of this statement
and of its similarity to the problems solved by Hermite and Lindemann,
I consider the proof of this theorem very difficult; as also the proof
that
The expression It is certain that the solution of these and
similar problems must lead us to entirely new methods and to a new insight
into the nature of special irrational and transcendental numbers.
all have the real part 1/2, except the well-known negative
integral real zeros. As soon as this proof has been successfully established,
the next problem would consist in testing more exactly Riemann's infinite
series for the number of primes below a given number and, especially, to
decide whether the difference between the number of primes below a number
x and the integral logarithm of x does in fact become infinite of an order
not greater than 1/2 in x.20
Further, we should determine whether the occasional condensation of prime
numbers which has been noticed in counting primes is really due to those
terms of Riemann's formula which depend upon the first complex zeros of
the function After an exhaustive discussion of Riemann's prime
number formula, perhaps we may sometime be in a position to attempt the
rigorous solution of Goldbach's problem,21
viz., whether every integer is expressible as the sum of two positive prime
numbers; and further to attack the well-known question, whether there are
an infinite number of pairs of prime numbers with the difference 2, or
even the more general problem, whether the linear diophantine equation
(with given integral coefficients each prime to the others) is always
solvable in prime numbers x and y.
But the following problem seems to me of no less
interest and perhaps of still wider range: To apply the results obtained
for the distribution of rational prime numbers to the theory of the distribution
of ideal primes in a given number-field k--a problem which looks toward
the study of the function where the sum extends over all ideals j of the given realm k, andn(j)
denotes
the norm of the ideal j.
I may mention three more special problems in
number theory: one on the laws of reciprocity, one on diophantine equations,
and a third from the realm of quadratic forms.
The law, as well as the means essential to its
proof, will, I believe, result by suitably generalizing the theory of the
field of the l-th roots of unity,22
developed by me, and my theory of relative quadratic fields.23
The following important problem may form a transition
to algebra and the theory of functions:
First. It answers the question as to the number
and existence of those equations which have a given degree, a given abelian
group and a given discriminant with respect to the realm of rational numbers.
Second. It states that the roots of such equations
form a realm of algebraic numbers which coincides with the realm obtained
by assigning to the argument z in the exponential function ei The first statement is concerned with the question
of the determination of certain algebraic numbers by their groups and their
branching. This question corresponds, therefore, to the known problem of
the determination of algebraic functions corresponding to given Riemann
surfaces. The second statement furnishes the required numbers by transcendental
means, namely, by the exponential function ei Since the realm of the imaginary quadratic number
fields is the simplest after the realm of rational numbers, the problem
arises, to extend Kronecker's theorem to this case. Kronecker himself has
made the assertion that the abelian equations in the realm of a quadratic
field are given by the equations of transformation of elliptic functions
with singular moduli, so that the elliptic function assumes here the same
role as the exponential function in the former case. The proof of Kronecker's
conjecture has not yet been furnished; but I believe that it must be obtainable
without very great difficulty on the basis of the theory of complex multiplication
developed by H. Weber25
with the help of the purely arithmetical theorems on class fields which
I have established.
Finally, the extension of Kronecker's theorem
to the case that, in place of the realm of rational numbers or of the
imaginary quadratic field, any algebraic field whatever is laid down as
realm of rationality, seems to me of the greatest importance. I regard
this problem as one of the most profound and far reaching in the theory
of numbers and of functions.
The problem is found to be accessible from many
standpoints. I regard as the most important key to the arithmetical part
of this problem the general law of reciprocity for residues of I-th
powers within any given number field.
As to the function-theoretical part of the problem,
the investigator in this attractive region will be guided by the remarkable
analogies which are noticeable between the theory of algebraic functions
of one variable and the theory of algebraic numbers. Hensel26
has proposed and investigated the analogue in the theory of algebraic numbers
to the development in power series of an algebraic function; and Landsberg27
has treated the analogue of the Riemann-Roch theorem. The analogy between
the deficiency of a Riemann surface and that of the class number of a field
of numbers is also evident. Consider a Riemann surface of deficiency p
= 1 (to touch on the simplest case only) and on the other hand a number
field of class h = 2. To the proof of the existence of an integral
everywhere finite on the Riemann surface, corresponds the proof of the
existence of an integer a in the number field such that the number The equation of Abel's theorem in the theory
of algebraic functions expresses, as is well known, the necessary and sufficient
condition that the points in question on the Riemann surface are the zero
points of an algebraic function belonging to the surface. The exact analogue
of Abel's theorem, in the theory of the number field of class h
= 2, is the equation of the law of quadratic reciprocity28
which declares that the ideal j is then and only then a principal
ideal of the number field when the quadratic residue of the number a
with respect to the ideal j is positive.
It will be seen that in the problem just sketched
the three fundamental branches of mathematics, number theory, algebra and
function theory, come into closest touch with one another, and I am certain
that the theory of analytical functions of several variables in particular
would be notably enriched if one should succeed in finding and discussing
those functions which play the part for any algebraic number field corresponding
to that of the exponential function in the field of rational numbers and
of the elliptic modular functions in the imaginary quadratic number field.
Passing to algebra, I shall mention a problem
from the theory of equations and one to which the theory of algebraic invariants
has led me.
Now it is probable that the root of the equation
of the seventh degree is a function of its coefficients which does not
belong to this class of functions capable of nomographic construction,
i.
e., that it cannot be constructed by a finite number of insertions
of functions of two arguments. In order to prove this, the proof would
be necessary that the equation of the seventh degree f7
+ xf3 + yf2 + zf + 1 = 0 is
not solvable with the help of any continuous functions of only two arguments.
I may be allowed to add that I have satisfied myself by a rigorous process
that there exist analytical functions of three arguments x, y, z
which cannot be obtained by a finite chain of functions of only two arguments.
By employing auxiliary movable elements, nomography
succeeds in constructing functions of more than two arguments, as d'Ocagne
has recently proved in the case of the equation of the 7-th degree.30
An important step in this direction had been
taken al ready by A. Hurwitz,32
who, by an ingenious process, succeeded in effecting the proof, in its
entire generality, of the finiteness of the system of orthogonal invariants
of an arbitrary ground form.
The study of the question as to the finiteness
of invariants has led me to a simple problem which includes that question
as a particular case and whose solution probably requires a decidedly more
minutely detailed study of the theory of elimination and of Kronecker's
algebraic modular systems than has yet been made.
Let a number m of integral rational functions
Xl,
X2,
... , Xm, of the n variables
xl,
x2, ... , xn be given,
The resulting problem is now to decide whether
it is always possible to find a finite system of relatively integral
function Xl, ... , Xmby which every
other relatively integral function ofXl, ... , Xmmay
be expressed rationally and integrally.
We can formulate the problem still more simply
if we introduce the idea of a finite field of integrality. By a finite
field of integrality I mean a system of functions from which a finite number
of functions can be chosen, in terms of which all other functions of the
system are rationally and integrally expressible. Our problem amounts,
then, to this: to show that all relatively integral functions of any given
domain of rationality always constitute a finite field of integrality.
It naturally occurs to us also to refine the
problem by restrictions drawn from number theory, by assuming the coefficients
of the given functions fl, ... , fm
to be integers and including among the relatively integral functions of
Xl,
... , Xm only such rational functions of these arguments
as become, by the application of the substitutions S, rational integral
functions of xl, ... , xn with rational
integral coefficients.
The following is a simple particular case of
this refined problem: Let m integral rational functions Xl,
... , Xm of one variable x with integral rational
coefficients, and a prime number p be given. Consider the system
of those integral rational functions of x which can be expressed
in the form
where G is a rational integral function of the arguments Xl,
... , Xm and ph is any power of the
prime number p. Earlier investigations of mine33
show immediately that all such expressions for a fixed exponent h
form a finite domain of integrality. But the question here is whether the
same is true for all exponents h, i. e., whether a finite
number of such expressions can be chosen by means of which for every exponent
h
every other expression of that form is integrally and rationally expressible.
From the boundary region between algebra and
geometry, I will mention two problems. The one concerns enumerative geometry
and the other the topology of algebraic curves and surfaces.
Although the algebra of today guarantees, in
principle, the possibility of carrying out the processes of elimination,
yet for the proof of the theorems of enumerative geometry decidedly more
is requisite, namely, the actual carrying out of the process of elimination
in the case of equations of special form in such a way that the degree
of the final equations and the multiplicity of their solutions may be foreseen.
In connection with this purely algebraic problem,
I wish to bring forward a question which, it seems to me, may be attacked
by the same method of continuous variation of coefficients, and whose answer
is of corresponding value for the topology of families of curves defined
by differential equations. This is the question as to the maximum number
and position of Poincaré's boundary cycles (cycles limites) for
a differential equation of the first order and degree of the form
where X and Y are rational integral functions of the n-th
degree in x and y. Written homogeneously, this is
where X, Y, and Z are rational integral homogeneous functions
of the n-th degree in x, y, z, and the latter are to be determined
as functions of the parameter t.
I mention one more geometrical problem:
Exactly the corresponding facts are found in
space of three dimensions. The fact of the finiteness of the groups of
motions in elliptic space is an immediate consequence of a fundamental
theorem of C. Jordan,40
whereby the number of essentially different kinds of finite groups of linear
substitutions in n variables does not surpass a certain finite limit
dependent upon n. The groups of motions with fundamental regions
in hyperbolic space have been investigated by Fricke and Klein in the lectures
on the theory of automorphic functions,41
and finally Fedorov,42
Schoenflies43and
lately Rohn44
have given the proof that there are, in euclidean space, only a finite
number of essentially different kinds of groups of motions with a fundamental
region. Now, while the results and methods of proof applicable to elliptic
and hyperbolic space hold directly for n-dimensional space also,
the generalization of the theorem for euclidean space seems to offer decided
difficulties. The investigation of the following question is therefore
desirable: Is there in n-dimensional euclidean space also only a finite
number of essentially different kinds of groups of motions with a fundamental
region?
A fundamental region of each group of motions,
together with the congruent regions arising from the group, evidently fills
up space completely. The question arises: whether polyhedra also exist
which do not appear as fundamental regions of groups of motions, by means
of which nevertheless by a suitable juxtaposition of congruent copies a
complete filling up of all space is possible. I point out the following
question, related to the preceding one, and important to number theory
and perhaps sometimes useful to physics and chemistry: How can one arrange
most densely in space an infinite number of equal solids of given form,
e.
g., spheres with given radii or regular tetrahedra with given edges
(or in prescribed position), that is, how can one so fit them together
that the ratio of the filled to the unfilled space may be as great as possible?
If we look over the development of the theory of functions in the last
century, we notice above all the fundamental importance of that class of
functions which we now designate as analytic functions--a class of functions
which will probably stand permanently in the center of mathematical interest.
There are many different standpoints from which
we might choose, out of the totality of all conceivable functions, extensive
classes worthy of a particularly thorough investigation. Consider, for
example, the class of functions characterized by ordinary or partial
algebraic differential equations. It should be observed that this class
does not contain the functions that arise in number theory and whose investigation
is of the greatest importance. For example, the before-mentioned function which stands in close relation with the function will have to be used.
If, on the other hand, we are lead by arithmetical
or geometrical reasons to consider the class of all those functions which
are continuous and indefinitely differentiable, we should be obliged in
its investigation to dispense with that pliant instrument, the power series,
and with the circumstance that the function is fully determined by the
assignment of values in any region, however small. While, therefore, the
former limitation of the field of functions was too narrow, the latter
seems to me too wide. The idea of the analytic function on the other hand
includes the whole wealth of functions most important to science whether
they have their origin in number theory, in the theory of differential
equations or of algebraic functional equations,whether they arise in geometry
or in mathematical physics; and, therefore, in the entire realm of functions,
the analytic function justly holds undisputed supremacy.
and certain linear differential equations investigated by Picard;46
also the equation
the partial differential equation of minimal surfaces, and others. Most
of these partial differential equations have the common characteristic
of being the lagrangian differential equations of certain problems of variation,
viz., of such problems of variation
as satisfy, for all values of the arguments which fall within the range
of discussion, the inequality
F itself being an analytic function. We shall call this sort
of problem a regular variation problem. It is chiefly the regular variation
problems that play a role in geometry, in mechanics, and in mathematical
physics; and the question naturally arises, whether all solutions of regular
variation problems must necessarily be analytic functions. In other words,
does
every lagrangian partial differential equation of a regular variation problem
have the property of admitting analytic integrals exclusively? And
is this the case even when the function is constrained to assume, as,
e.
g., in Dirichlet's problem on the potential function, boundary values
which are continuous, but not analytic?
I may add that there exist surfaces of constant
negative
gaussian curvature which are representable by functions that are continuous
and possess indeed all the derivatives, and yet are not analytic; while
on the other hand it is probable that every surface whose gaussian curvature
is constant and positive is necessarily an analytic surface. And we know
that the surfaces of positive constant curvature are most closely related
to this regular variation problem: To pass through a closed curve in space
a surface of minimal area which shall inclose, in connection with a fixed
surface through the same closed curve, a volume of given magnitude.
In conjunction with this problem comes up the
problem of reducing to uniformity an algebraic or any other analytic relation
among three or more complex variables--a problem which is known to be solvable
in many particular cases. Toward the solution of this the recent investigations
of Picard on algebraic functions of two variables are to be regarded as
welcome and important preliminary studies.
The lack of interest in this is perhaps due in
part to the need of reliable modern text books. So much the more praiseworthy
is it that A. Kneser in a very recently published work has treated the
calculus of variations from the modern points of view and with regard to
the modern demand for rigor.51
The calculus of variations is, in the widest
sense, the theory of the variation of functions, and as such appears as
a necessary extension of the differential and integral calculus. In this
sense, Poincaré's investigations on the problem of three bodies,
for example, form a chapter in the calculus of variations, in so far as
Poincaré derives from known orbits by the principle of variation
new orbits of similar character.
I add here a short justification of the general
remarks upon the calculus of variations made at the beginning of my lecture.
The simplest problem in the calculus of variations
proper is known to consist in finding a function y of a variable
x
such that the definite integral
assumes a minimum value as compared with the values it takes when y
is replaced by other functions of x with the same initial and final
values.
The vanishing of the first variation in the usual
sense
gives for the desired function y the well-known differential
equation
where A and B do not contain y, and the vanishing
of the first variation
in the sense which the new question requires gives the equation
i. e., we obtain for the function p of the two variables
x,
y the partial differential equation of the first order
which also admits these integral curves as solutions, then the function
p(x,
y) is always an integral of the partial differential equation (1*)
of the first order; and conversely, if p(x, y) denotes any
solution of the partial differential equation (1*) of the first order,
all the non-singular integrals of the ordinary differential equation (2)
of the first order are at the same time integrals of the differential equation
(l) of the second order, or in short if yx =
p(x,
y) is an integral equation of the first order of the differential equation
(l) of the second order, p(x, y) represents an integral of
the partial differential equation (1*) and conversely; the integral curves
of the ordinary differential equation of the second order are therefore,
at the same time, the characteristics of the partial differential equation
(1*) of the first order.
In the present case we may find the same result
by means of a simple calculation; for this gives us the differential equations
(1) and (1*) in question in the form
where the lower indices indicate the partial derivatives with respect
to x, y, p, yx. The correctness of the affirmed relation
is clear from this.
The close relation derived before and just proved
between the ordinary differential equation (1) of the second order and
the partial differential equation (1*) of the first order, is, as it seems
to me, of fundamental significance for the calculus of variations. For,
from the fact that the integral J* is independent of the path of
integration it follows that
if we think of the left hand integral as taken along any path y
and the right hand integral along an integral curve where E designates Weierstrass's expression, depending upon yx,
p, y, x,
The developments indicated may be transferred
without necessitating further calculation to the case of two or more required
functions, and also to the case of a double or a multiple integral. So,
for example, in the case of a double integral
to be extended over a given region gives the well-known differential equation of the second order
for the required function z of x and y.
On the other hand we consider the integral
and inquire, how p and q are to be taken as functions of x, y and
z in order that the value of this integral may be independent of the choice
of the surface passing through the given closed twisted curve, i. e., of
the choice of the function z of the variables x and y.
The integral J* has the form
>and the vanishing of the first variation
in the sense which the new formulation of the question demands, gives
the equation
i. e., we find for the functions p and q of the
three variables x, y and z the differential equation of the
first order
resulting from the equations
the partial differential equation (I) for the function z of the
two variables x and y and the simultaneous system of the
two partial differential equations of the first order (I*) for the two
functions p and q of the three variables x, y, and
z
stand toward one another in a relation exactly analogous to that in which
the differential equations (1) and (1*) stood in the case of the simple
integral.
It follows from the fact that the integral J*
is independent of the choice of the surface of integration z that
if we think of the right hand integral as taken over an integral surface
z
of the partial differential equations
and with the help of this formula we arrive at once at the formula
which plays the same role for the variation of double integrals as the
previously given formula (4) for simple integrals. With the help of this
formula we can now answer the question how far Jacobi's condition in conjunction
with Weierstrass's condition E > 0 is necessary and sufficient for
the occurrence of a minimum.
Connected with these developments is the modified
form in which A. Kneser,52
beginning from other points of view, has presented Weierstrass's theory.
While Weierstrass employed integral curves of equation (1) which pass through
a fixed point in order to derive sufficient conditions for the extreme
values, Kneser on the other hand makes use of any simple family of such
curves and constructs for every such family a solution, characteristic
for that family, of that partial differential equation which is to be considered
as a generalization of the Jacobi-Hamilton equation.
The problems mentioned are merely samples of problems, yet they will
suffice to show how rich, how manifold and how extensive the mathematical
science of today is, and the question is urged upon us whether mathematics
is doomed to the fate of those other sciences that have split up into separate
branches, whose representatives scarcely understand one another and whose
connection becomes ever more loose. I do not believe this nor wish it.
Mathematical science is in my opinion an indivisible whole, an organism
whose vitality is conditioned upon the connection of its parts. For with
all the variety of mathematical knowledge, we are still clearly conscious
of the similarity of the logical devices, the relationship of the ideas
in mathematics as a whole and the numerous analogies in its different departments.
We also notice that, the farther a mathematical theory is developed, the
more harmoniously and uniformly does its construction proceed, and unsuspected
relations are disclosed between hitherto separate branches of the science.
So it happens that, with the extension of mathematics, its organic character
is not lost but only manifests itself the more clearly.
But, we ask, with the extension of mathematical
knowledge will it not finally become impossible for the single investigator
to embrace all departments of this knowledge? In answer let me point out
how thoroughly it is ingrained in mathematical science that every real
advance goes hand in hand with the invention of sharper tools and simpler
methods which at the same time assist in understanding earlier theories
and cast aside older more complicated developments. It is therefore possible
for the individual investigator, when he makes these sharper tools and
simpler methods his own, to find his way more easily in the various branches
of mathematics than is possible in any other science.
The organic unity of mathematics is inherent
in the nature of this science, for mathematics is the foundation of all
exact knowledge of natural phenomena. That it may completely fulfil this
high mission, may the new century bring it gifted masters and many zealous
and enthusiastic disciples!
The original address "Mathematische
Probleme" appeared in Göttinger Nachrichten, 1900, pp. 253-297,
and in Archiv der Mathematik und Physik, (3) 1 (1901), 44-63 and
213-237. [A fuller title of the journal Göttinger Nachrichten
is Nachrichten von der Königl. Gesellschaft der Wiss. zu Göttingen.]
The French translation by M. L.
Laugel "Sur les problèmes futurs des mathématiques" appeared
in Compte Rendu du Deuxième Congrès International des
Mathématiciens, pp. 58-114, Gauthier-Villars, Paris, 1902.
This HTML version of Newson's translation
was prepared for the web by D
Joyce with only minor modifications, mainly, more complete references.
2
H. Minkowski: Die Geometrie der Zahlen. Teubner, Leipzig, 1896.
3
See Helmholtz, Ueber die Wechselwirkung der Natnrkräefte und die
darauf bezüglichen neuesten Ermittelungen der Physik. Vortrag
gehalten Köigsberg, 1854.
4
P. Gordon: "Über homogene Functionen," Jahresbericht der Deutchen
Mathematiker-Vereinigung 8 (1900), p. 180.
5
Gauss Werke, vol. 8, pp. 241 and 244.
6
Cf., beside earlier literature, Hilbert, Grundlagen der Geometrie,
Teubner, Leipzig, 1899, ch. 4. [Translated as Foundations of Geometry
by Townsend, Open Court, Chicago, 1902.]
7
Since this was written M. Dehn has succeeded in proving this impossibility.
See his note: "Ueber raumgleishe Polyeder," in Gött. Nachrichten,
1900, pp. 345-354, and a paper [then] soon to appear in Math. Annalen
["Ueber den Rauminhalt," 55 (1902), 465-478].
8
H. Minkowski: Die Geometrie der Zahlen. Teubner, Leipzig, 1896.
9
D. Hilbert. "Ueber die gerade Linie als kürzeste Verbindung zweier
Punkte," Math. Annalen, 46 (1895), 91-96.
10
S. Lie and F. Engel, Theorie der Transformationsgruppen, vol. 3,
Teubner, Leipzig, 1893, §§ 82 and 144.
11
F. Schur: "Ueber den analytischen Charakter der eine endliche continuierliche
Transformationgruppe darstellenden Functionen, " Math. Annalen 41
(1893), 509-538.
12
Abel: Werke, vol. 1, pp. 1, 61, 389.
13
É. Picard: "Quelques théories fondamentales dans l'analyse
mathématique," Conférences faites à Clark University,
Revue
générale des Sciences, 1900, p. 22.
14
Cf. G. Bohlmann, "Ueber Versicherungsmathematik," from the collection:
F. Klein and E. Riecke, Ueber angewandte Mathematik und Physik,
Teubner, Leipzig, 1900.
15
E. Mach: Die Mechanik in ihrer Entwickelnng, Brockhaus, Leipzig,
4th edition, 1901.
16
H. Hertz: Die Prinzipien der Mechanik, Leipzig, 1894.
17
L. Boltzmann: Vorlesungen über die Principe der Mechanik, Leipzig,
1897.
18
P. Volkmann: Einführung in das Studium der theoretischen Physik,
Teubner, Leipzig, 1900.
19
A. Hurwitz: Math. Annalen 22 (1883), 211-229, and 32 (1888), 583-588.
20
Cf. an article by H. von Koch, which is soon to appear in Math. Annalen
["Ueber die Riemann'sche Primzahlfunction," 55 (1902), 441-464].
21
Cf. M.-P. Stackel: "Über Goldbach's empirisches Theorem," Gött.
Nachrichten, 1896, and Landau, ibid., 1900.
22
D. Hilbert: Jahresber. d. Deutschen Math.-Vereinigung, "Ueber die
Theorie der algebraischen Zahlkörper," 4 (1897), Part V (pp. 175-546).
23
D. Hilbert: "Ueber die Theorie des relativquadratischen Zalhkörpers,"
Math.
Annalen 51 (1899), 1-127, and Gött. Nachrichten, 1898.
24
D. Hilbert, "Ueber den Dirichlet'schen biquadratischen Zahlenkörper,"
Math.
Annalen, 45(1884); "Ueber die Theorie der relativquadratischen Zahlkörper,"
Jahresber.
d. Deutschen Mathematiker-Vereinigung 6 (1897), 88-94, and Math.
Annalen, 51 (1899); "Ueber die Theorie der relativ-Abel'schen Zahlkörper,"
Gött. Nachrichten, 1898, pp. 370-399; Grundlagen der Geometrie,
Leipzig, 1899, Chap. VIII, § 83 [Translation by Townsend, Chicago,
1902]. Cf. also the dissertation of G. Ruckle, Göttingen, 1901.
25
H. Weber: Elliptische Functionen und algebraische Zahlen. Vieweg,
Braunschweig, 1891.
26
K. Hensel: "Über eine neue Begründung der Theorie der algebraischen
Zalen," Jahresber. d . Deutschen Math.-Vereinigung 6 (1897), 83-88,
and an article soon to appear in Math. Annalen [55, (1902), 301]:
"Ueber die Entwickelung der algebraischen Zahlen in Potenzreihen."
27
G. Landsberg: "Ueber das Analogon des Riemann-Roch'schen Satzes in der
Theorie der algebraischen Zalen," Math. Annalen 50 (1898), 577-582.
28
Cf. Hilbert, "Ueber die Theorie der relativ-Abelschen Zahlkörper,"
Gött.
Nachrichten, 1898, pp. 370-399.
29
M. d'Ocagne, Traité de Nomographie, Gauyhier-Villars, Paris,
1899.
30
M. d'Ocagne: "Sur la résolution nomographique de l'équation
du septième degré." Comptes rendus Paris, 131 (1900),
522-524.
31
Cf. L. Murer: Sitzungsber. d. K. Acad. d. Wiss. zu München,
1899, and an article about to appear in Math. Annalen.
32
A. Hurwitz: "Ueber die Erzeugung der Invarianten durch Integration," Gött.
Nachrichten, 1897, pp. 71-90.
33
D. Hilbert: "Ueber die Theorie der algebraischen Formen," Math. Annalen,
36 (1890), 473-534.
34
H. Schubert: Kalkül der abzählenden Geometrie, Teubner,
Leipzig, 1879.
35
Harnack: "Ueber die Vieltheiligkeit der ebenen algebraischen Curven," Math.
Annalen, 10 (1876), 189-198.
36
Cf. K. Rohn, "Flächen vierter Ordnung," Preisschriften der Fürstlich
Jablonowskischen Gesellschaft, Leipzig, 1886.
37
D. Hilbert: "Ueber die Darstellung definiter Formen als Summen von Formenquadraten,"
Math.
Annalen, 32 (1888), 342-350.
38
D. Hilbert: "Über ternäre definite Formen," Acta Mathematica,
17 (1893), 169-198.
39
Cf. Hilbert Grundlagen der Geometrie, Leipzig, 1899, Chap. 7 and
in particular §38.
40
C. Jordan: "Mémoire sur les équations différentielles
linéaires à intégrale algébrique," [Crelle's]
Journal für die Reine und Angew. Math. 84 (1879), and Atti
d. Reale Acad. di Napoli, 1880.
41
R. Fricke and F. Klein: Vorlesungen über die Theoire der automorphen
Functionen, Teubner, Leipzig, 1897. Cf. especially Abschnitt I, Chapters
2 and 3.
42
E. Fedorov: Symmetrie der regelmässigen Systeme von Figuren,
l890.
43
A. Schoenflies: Krystallsysteme und Krystallstruktur, Teubner, Leipzig,
1891.
44
K. Rohn: "Einige Sätze über regelmässige Punktgruppen,"
Math.
Annalen, 53 (1900), 440-449.
45
Hölder: "Uber die Eigenschaft der Gammafunction keiner algebraischen
Differentialgleichung zu genügen," Math. Annalen, 28 (1887),
1-13.
46
Picard: Jour. de l'Ecole Polytech., 1890.
47
Cf. D. Hilbert: "Über das Dirichlet'sche Princip," Jahresber. d.
Deutschen Math.-Vereinigung, 8 (1900), 184-188.
48
L. Schlesinger: Handbuch der Theorie der linearen Differentialgleichungen,
vol. 2, part 2, No. 366.
49
H. Poincaré: "Sur un théorème de la théorie
générale des fonctions," BuII. de la Soc. Math. de France,
11 (1883),112-125.
50
Text-books: Moigno and Lindelöf, Leçons du calcul des variations,
Mallet-Bachelier, Paris, 1861, and A. Kneser, Lehrbuch der Variations-rechnung,
Vieweg, Braunschweig, 1900.
51
As an indication of the contents of this work, it may here be noted that
for the simplest problems Kneser derives sufficient conditions of the extreme
even for the case that one limit of integration is variable, and employs
the envelope of a family of curves satisfying the differential equations
of the problem to prove the necessity of Jacobi's conditions of the extreme.
Moreover, it should be noticed that Kneser applies Weierstrass's theory
also to the inquiry for the extreme of such quantities as are defined by
differential equations.
52
Cf. Kneser's above-mentioned textbook, §§ 14, 16, 19 and 20.
7. Irrationality
and transcendence of certain numbers
Hermite's arithmetical theorems on the exponential function and their extension
by Lindemann are certain of the admiration of all generations of mathematicians.
Thus the task at once presents itself to penetrate further along the path
here entered, as A. Hurwitz has already done in two interesting papers,19
"Ueber arithmetische Eigenschaften gewisser transzendenter Funktionen."
I should like, therefore, to sketch a class of problems which, in my opinion,
should be attacked as here next in order. That certain special transcendental
functions, important in analysis, take algebraic values for certain algebraic
arguments, seems to us particularly remarkable and worthy of thorough investigation.
Indeed, we expect transcendental functions to assume, in general, transcendental
values for even algebraic arguments; and, although it is well known that
there exist integral transcendental functions which even have rational
values for all algebraic arguments, we shall still con sider it highly
probable that the exponential function ei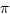 z,
for example, which evidently has algebraic values for all rational arguments
z,
will on the other hand always take transcendental values for irrational
algebraic values of the argument z. We can also give this statement
a geometrical form, as follows:
z,
for example, which evidently has algebraic values for all rational arguments
z,
will on the other hand always take transcendental values for irrational
algebraic values of the argument z. We can also give this statement
a geometrical form, as follows:
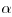
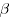 ,
for an algebraic base
,
for an algebraic base 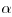 and an irrational algebraic exponent
and an irrational algebraic exponent 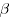 ,
e. g., the number 2
,
e. g., the number 2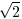 or e
or e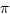 = i-2i, always represents a transcendental
or at least an irrational number.
= i-2i, always represents a transcendental
or at least an irrational number.
8. Problems of prime numbers
Essential progress in the theory of the distribution of prime numbers has
lately been made by Hadamard, de la Vallée-Poussin, Von Mangoldt
and others. For the complete solution, however, of the problems set us
by Riemann's paper "Ueber die Anzahl der Primzahlen unter einer gegebenen
Grösse," it still remains to prove the correctness of an exceedingly
important statement of Riemann, viz., that the zero points of the function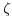 (s)
defined
by the series
(s)
defined
by the series
![[definition of the Riemann zeta function]](disp1.gif)
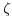 (s).
(s).
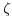 k(s)
belonging
to the field and defined by the series
k(s)
belonging
to the field and defined by the series
![[definition of the zeta_k function]](disp2.gif)
9. Proof
of the most general law of reciprocity in any number field
For any field of numbers the law of reciprocity is to be proved for
the residues of the l-th power, when l denotes an odd prime,
and further when l is a power of 2 or a power of an odd prime.
10. Determination
of the solvability of a diophantine equation
Given a diophantine equation with any number of unknown quantities and
with rational integral numerical coefficients: to devise a process according
to which it can be determined by a finite number of operations whether
the equation is solvable in rational integers.
11. Quadratic
forms with any algebraic numerical coefficients
Our present knowledge of the theory of quadratic number fields24
puts us in a position to attack successfully the theory of quadratic
forms with any number of variables and with any algebraic numerical coefficients.
This leads in particular to the interesting problem: to solve a given quadratic
equation with algebraic numerical coefficients in any number of variables
by integral or fractional numbers belonging to the algebraic realm of rationality
determined by the coefficients.
12. Extension
of Kronecker's theorem on abelian fields to any realm of algebraic rationality
The theorem that every abelian number field arises from the realm of rational
numbers by the composition of fields of roots of unity is due to Kronecker.
This fundamental theorem in the theory of integral equations contains two
statements, namely:
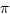 z
all rational numerical values in succession.
z
all rational numerical values in succession.
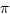 z.
z.
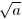 represents a quadratic field, relatively unbranched with respect to the
fundamental field. In the theory of algebraic functions, the method of
boundary values (Randwerthaufgabe) serves, as is well known, for
the proof of Riemann's existence theorem. In the theory of number fields
also, the proof of the existence of just this number a offers the
greatest difficulty. This proof succeeds with indispensable assistance
from the theorem that in the number field there are always prime ideals
corresponding to given residual properties. This latter fact is therefore
the analogue in number theory to the problem of boundary values.
represents a quadratic field, relatively unbranched with respect to the
fundamental field. In the theory of algebraic functions, the method of
boundary values (Randwerthaufgabe) serves, as is well known, for
the proof of Riemann's existence theorem. In the theory of number fields
also, the proof of the existence of just this number a offers the
greatest difficulty. This proof succeeds with indispensable assistance
from the theorem that in the number field there are always prime ideals
corresponding to given residual properties. This latter fact is therefore
the analogue in number theory to the problem of boundary values.
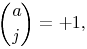
13. Impossibility
of the solution of the general equation of the 7-th degree by means of
functions of only two arguments
Nomography29
deals with the problem: to solve equations by means of drawings of families
of curves depending on an arbitrary parameter. It is seen at once that
every root of an equation whose coefficients depend upon only two parameters,
that is, every function of two independent variables, can be represented
in manifold ways according to the principle lying at the foundation of
nomography. Further, a large class of functions of three or more variables
can evidently be represented by this principle alone without the use of
variable elements, namely all those which can be generated by forming first
a function of two arguments, then equating each of these arguments to a
function of two arguments, next replacing each of those arguments in their
turn by a function of two arguments, and so on, regarding as admissible
any finite number of insertions of functions of two arguments. So, for
example, every rational function of any number of arguments belongs to
this class of functions constructed by nomographic tables; for it can be
generated by the processes of addition, subtraction, multiplication and
division and each of these processes produces a function of only two arguments.
One sees easily that the roots of all equations which are solvable by radicals
in the natural realm of rationality belong to this class of functions;
for here the extraction of roots is adjoined to the four arithmetical operations
and this, indeed, presents a function of one argument only. Likewise the
general equations of the 5-th and 6-th degrees are solvable by suitable
nomographic tables; for, by means of Tschirnhausen transformations, which
require only extraction of roots, they can be reduced to a form where the
coefficients depend upon two parameters only.
14. Proof
of the finiteness of certain complete systems of functions
In the theory of algebraic invariants, questions as to the finiteness of
complete systems of forms deserve, as it seems to me, particular interest.
L. Maurer31
has lately succeeded in extending the theorems on finiteness in invariant
theory proved by P. Gordan and myself, to the case where, instead of the
general projective group, any subgroup is chosen as the basis for the definition
of invariants.
(S)
X1 = f1(x1,
... , xn),
X2 = f2(x1, ...
, xn),
...
Xm = fm(x1, ...
, xn).
15. Rigorous
foundation of Schubert's enumerative calculus
The problem consists in this: To establish rigorously and with an exact
determination of the limits of their validity those geometrical numbers
which Schubert34
especially has determined on the basis of the so-called principle of special
position, or conservation of number, by means of the enumerative calculus
developed by him.
16. Problem
of the topology of algebraic curves and surfaces
The maximum number of closed and separate branches which a plane algebraic
curve of the n-th order can have has been determined by Harnack.35
There arises the further question as to the relative position of the branches
in the plane. As to curves of the 6-th order, I have satisfied myself--by
a complicated process, it is true--that of the eleven branches which they
can have according to Harnack, by no means all can lie external to one
another, but that one branch must exist in whose interior one branch and
in whose exterior nine branches lie, or inversely. A thorough investigation
of the relative position of the separate branches when their number is
the maximum seems to me to be of very great interest, and not less so the
corresponding investigation as to the number, form, and position of the
sheets of an algebraic surface in space. Till now, indeed, it is not
even known what is the maxi mum number of sheets which a surface of the
4-th order in three dimensional space can really have.36
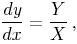
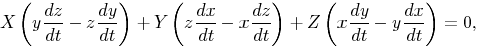
17. Expression of definite
forms by squares
A rational integral function or form in any number of variables with real
coefficient such that it becomes negative for no real values of these variables,
is said to be definite. The system of all definite forms is invariant with
respect to the operations of addition and multiplication, but the quotient
of two definite forms--in case it should be an integral function of the
variables--is also a definite form. The square of any form is evidently
always a definite form. But since, as I have shown,37
not every definite form can be compounded by addition from squares of forms,
the question arises--which I have answered affirmatively for ternary forms38--whether
every definite form may not be expressed as a quotient of sums of squares
of forms. At the same time it is desirable, for certain questions as to
the possibility of certain geometrical constructions, to know whether the
coefficients of the forms to be used in the expression may always be taken
from the realm of rationality given by the coefficients of the form represented.39
18. Building up of space from congruent polyhedra
If we enquire for those groups of motions in the plane for which a fundamental
region exists, we obtain various answers, according as the plane considered
is Riemann's (elliptic), Euclid's, or Lobachevsky's (hyperbolic). In the
case of the elliptic plane there is a finite number of essentially different
kinds of fundamental regions, and a finite number of congruent regions
suffices for a complete covering of the whole plane; the group consists
indeed of a finite number of motions only. In the case of the hyperbolic
plane there is an infinite number of essentially different kinds of fundamental
regions, namely, the well-known Poincaré polygons. For the complete
covering of the plane an infinite number of congruent regions is necessary.
The case of Euclid's plane stands between these; for in this case there
is only a finite number of essentially different kinds of groups of motions
with fundamental regions, but for a complete covering of the whole plane
an infinite number of congruent regions is necessary.
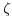 (s)
satisfies no algebraic differential equation, as is easily seen with the
help of the well-known relation between
(s)
satisfies no algebraic differential equation, as is easily seen with the
help of the well-known relation between 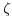 (s)
and
(s)
and 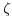 (1 - s),
if one refers to the theorem proved by Hölder,45
that the function
(1 - s),
if one refers to the theorem proved by Hölder,45
that the function  (x)
satisfies no algebraic differential equation. Again, the function of the
two variables s and l defined by the infinite series
(x)
satisfies no algebraic differential equation. Again, the function of the
two variables s and l defined by the infinite series
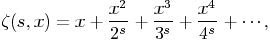
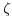 (s),
probably satisfies no algebraic partial differential equation. In the investigation
of this question the functional equation
(s),
probably satisfies no algebraic partial differential equation. In the investigation
of this question the functional equation
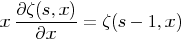
19. Are
the solutions of regular problems in the calculus of variations always
necessarily analytic?
One of the most remarkable facts in the elements of the theory of analytic
functions appears to me to be this: That there exist partial differential
equations whose integrals are all of necessity analytic functions of the
independent variables, that is, in short, equations susceptible of none
but analytic solutions. The best known partial differential equations of
this kind are the potential equation
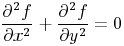
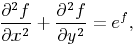
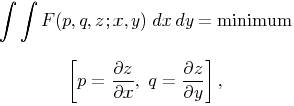
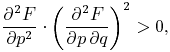
20. The general problem
of boundary values
An important problem closely connected with the foregoing is the question
concerning the existence of solutions of partial differential equations
when the values on the boundary of the region are prescribed. This problem
is solved in the main by the keen methods of H. A. Schwarz, C. Neumann,
and Poincaré for the differential equation of the potential. These
methods, however, seem to be generally not capable of direct extension
to the case where along the boundary there are prescribed either the differential
coefficients or any relations between these and the values of the function.
Nor can they be extended immediately to the case where the inquiry is not
for potential surfaces but, say, for surfaces of least area, or surfaces
of constant positive gaussian curvature, which are to pass through a prescribed
twisted curve or to stretch over a given ring surface. It is my conviction
that it will be possible to prove these existence theorems by means of
a general principle whose nature is indicated by Dirichlet's principle.
This general principle will then perhaps enable us to approach the question:
Has
not every regular variation problem a solution, provided certain assumptions
regarding the given boundary conditions are satisfied (say that the
functions concerned in these boundary conditions are continuous and have
in sections one or more derivatives), and provided also if need be that
the notion of a solution shall be suitably extended?47
21. Proof
of the existence of linear differential equations having a prescribed monodromic
group
In the theory of linear differential equations with one independent variable
z,
I wish to indicate an important problem one which very likely Riemann himself
may have had in mind. This problem is as follows: To show that there
always exists a linear differential equation of the Fuchsian class, with
given singular points and monodromic group. The problem requires the
production of n functions of the variable z, regular throughout
the complex z-plane except at the given singular points; at these
points the functions may become infinite of only finite order, and when
z
describes circuits about these points the functions shall undergo the prescribed
linear substitutions. The existence of such differential equations has
been shown to be probable by counting the constants, but the rigorous proof
has been obtained up to this time only in the particular case where the
fundamental equations of the given substitutions have roots all of absolute
magnitude unity. L. Schlesinger has given this proof,48
based upon Poincaré's theory of the Fuchsian  -functions.
The theory of linear differential equations would evidently have a more
finished appearance if the problem here sketched could be disposed of by
some perfectly general method.
-functions.
The theory of linear differential equations would evidently have a more
finished appearance if the problem here sketched could be disposed of by
some perfectly general method.
22. Uniformization of analytic relations by means of automorphic functions
As Poincaré was the first to prove, it is always possible to reduce
any algebraic relation between two variables to uniformity by the use of
automorphic functions of one variable. That is, if any algebraic equation
in two variables be given, there can always be found for these variables
two such single valued automorphic functions of a single variable that
their substitution renders the given algebraic equation an identity. The
generalization of this fundamental theorem to any analytic non-algebraic
relations whatever between two variables has likewise been attempted with
success by Poincaré,49
though by a way entirely different from that which served him in the special
problem first mentioned. From Poincaré's proof of the possibility
of reducing to uniformity an arbitrary analytic relation between two variables,
however, it does not become apparent whether the resolving functions can
be determined to meet certain additional conditions. Namely, it is not
shown whether the two single valued functions of the one new variable can
be so chosen that, while this variable traverses the regular domain of
those functions, the totality of all regular points of the given analytic
field are actually reached and represented. On the contrary it seems to
be the case, from Poincaré's investigations, that there are beside
the branch points certain others, in general infinitely many other discrete
exceptional points of the analytic field, that can be reached only by making
the new variable approach certain limiting points of the functions. In
view of the fundamental importance of Poincaré's formulation of
the question it seems to me that an elucidation and resolution of this
difficulty is extremely desirable.
23. Further
development of the methods of the calculus of variations
So far, I have generally mentioned problems as definite and special as
possible, in the opinion that it is just such definite and special problems
that attract us the most and from which the most lasting influence is often
exerted upon science. Nevertheless, I should like to close with a general
problem, namely with the indication of a branch of mathematics repeatedly
mentioned in this lecture--which, in spite of the considerable advancement
lately given it by Weierstrass, does not receive the general appreciation
which, in my opinion, is its due--I mean the calculus of variations.50
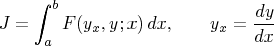
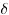 J = 0
J = 0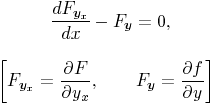
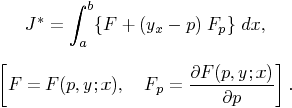
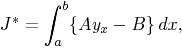
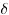 J* = 0
J* = 0
(2)
(1)
(1*)
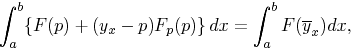
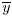 of the differential equation
of the differential equation
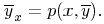
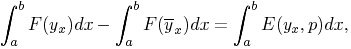
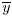 ,
which we are considering, the developments just indicated lead immediately--without
the introduction of the second variation, but only by the application of
the polar process to the differential equation (1)--to the expression of
Jacobi's condition and to the answer to the question: How far this condition
of Jacobi's in conjunction with Weierstrass's condition E > 0 is
necessary and sufficient for the occurrence of a minimum.
,
which we are considering, the developments just indicated lead immediately--without
the introduction of the second variation, but only by the application of
the polar process to the differential equation (1)--to the expression of
Jacobi's condition and to the answer to the question: How far this condition
of Jacobi's in conjunction with Weierstrass's condition E > 0 is
necessary and sufficient for the occurrence of a minimum.
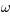 ,
the vanishing of the first variation (to be understood in the usual sense)
,
the vanishing of the first variation (to be understood in the usual sense)
 J = 0
J = 0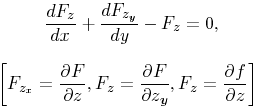
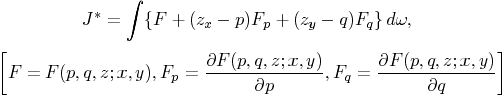
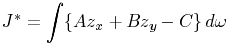
 J = 0
J = 0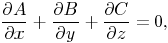
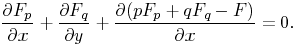
(I*)
zy = q(x, y, z)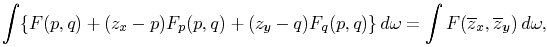
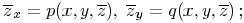
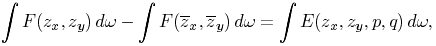
[E(zx, zy, p, q) = F(zx,
zy) - F(p, q) - (zx - p)Fp(p,
q) -
(zy - q)Fq(p)Fp(p,
q)],
Notes