
Ahora toma el tablero de ajedrez y tapa con dos monedas los dos cuadros de dos esquinas opuestas. Se trata ahora de cubrir todos los demás con las 31 fichas de dominó, cada ficha ocupando dos cuadros contiguos del ajedrez.
Si se te ocurre que te engaño, trata de probar que el juego es imposible. Te daré una pista. El juego del ajedrez es muy grande, con sus 64 cuadros. ¿Por qué no ensayas primero con un tablero de menos cuadros, por ejemplo con uno 6 x 6 y con 17 fichas de dominó o con uno aún más pequeño?
Ahora cierra estas páginas y
manos a la obra. Prueba un rato antes de volver...
Sí. Efectivamente, el juego es imposible. Seguro que si has empezado con el caso más sencillo te habrás dado cuenta enseguida.
El tablero de cuatro cuadros, después de ponerle dos monedas en dos esquinas opuestas, queda así:

Es claro que no hay forma de colocar una ficha de dominó que cubra los dos cuadros que quedan.
Con un tablero de 9 cuadros el juego no tiene sentido, pues al cubrir 2 quedan 7 y con 3 fichas de dominó cubriríamos 6 y con 4 cubriríamos 8.
En el tablero de 16 cuadros
 |
la cosa no es tan obvia, pero tal vez el caso de los cuatro cuadros te ha dado la idea. Al empezar hemos tapado con monedas dos cuadros negros del tablero. Quedan entonces por tapar 8 cuadros blancos y 6 cuadros negros. ¡Pero cada ficha de dominó cubre necesariamente un cuadro blanco y otro negro! Así, si fuésemos capaces de colocar las siete fichas de dominó estaríamos cubriendo siete cuadros blancos y siete negros. El solitario es imposible.
El caso de 64 cuadros o de 100 cuadros es exactamente igual. Como ves, empezar por los casos sencillos puede aclarar mucho las cosas.
Para hacer las cosas más complicadas vamos a demostrar lo mismo utilizando el grupo de Klein, siguiendo la idea del solitario del caballero de la Bastilla. Escribimos en el tablero de ajedrez los siguientes elementos del grupo de Klein:
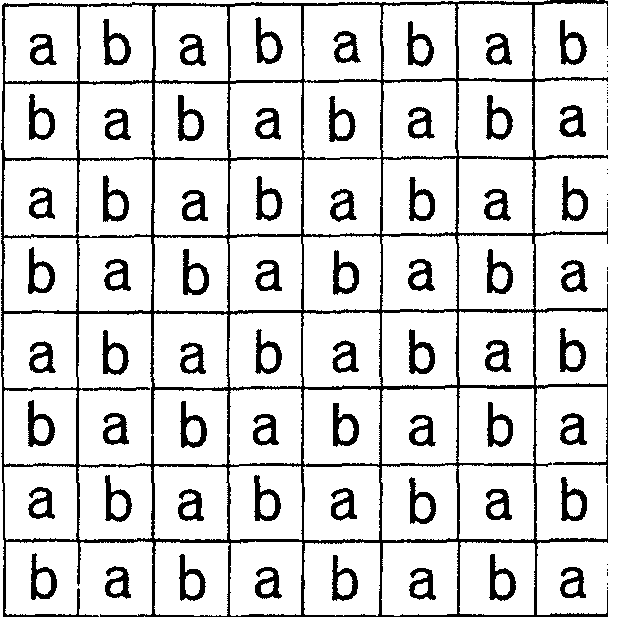
El producto de todos los elementos es a32 b 32 = 1. Si quitamos dos esquinas opuestas (o dos cuadrados del mismo color, por ejemplo dos cuadrados con b) el producto es también 1, pues será a a32 b 30 =1. Si interpretamos el colocar una ficha de dominó como dividir por los elementos del grupo que la ficha tapa, colocar una ficha es dividir por ab. Así, colocar 31 fichas es dividir a32 b 30 por a31b 31, es decir, el resultado es ab. Pero si hubiéramos cubierto todos los cuadros exactamente, el producto sería 1. Así, el juego es imposible. Es decir, si las monedas iniciales se colocan en dos cuadros del mismo color, el solitario es imposible.
¿Y si cubrimos inicialmente con las dos monedas dos cuadros de distinto color? Ninguno de nuestros razonamientos demuestra ahora la imposibilidad del solitario. Con el razonamiento del grupo de Klein estamos dividiendo por ab y así queda a31 b 31= ab. Colocar 31 fichas de dominó es dividir por a31 b 31 y así queda 1, que es lo que debería quedar con el tablero todo cubierto exactamente.
¿Será ahora el solitario
así propuesto posible o imposible? ¿Por qué no pruebas
antes de pasar adelante ensayando unos cuantos casos particulares? ¿En
tableros reducidos? Si es posible, ¿podrías dar con una receta
para resolver el solitario cuando se puede hacer?
El solitario así propuesto es posible y aquí tienes dos recetas. La primera es mía y la segunda de R. Gomory, un matemático de IBM.
Suponte que hay uno de los dos cuadros tapados c1, c2, que no está en uno de los bordes del tablero (el caso en que los dos están en los bordes es fácil, siguiendo la misma idea, y te lo dejo para ti). Sea ese cuadro c1. Escoge una región del tablero determinada por c1 y un borde de tal modo que en ella no esté c2, tal como te indico aquí:
Ahora escoge el camino serpenteante
que te indico por los cuadros del tablero hasta un rincón
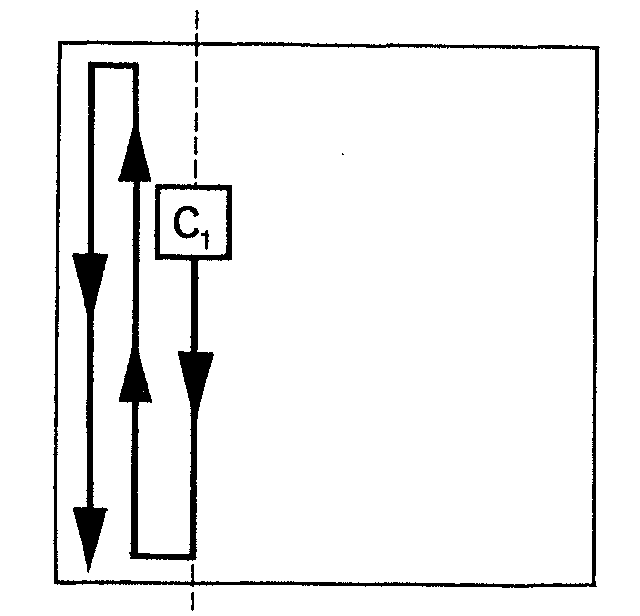 |
Este camino atraviesa un número par o impar de cuadros. Si es impar, entonces el camino opuesto siguiente
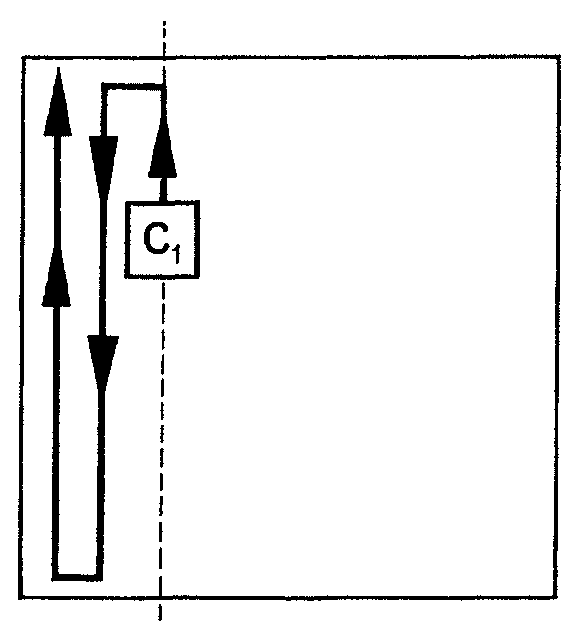
atraviesa un número par de cuadros. Escogemos el camino con un número par de cuadros y lo rellenamos ordenadamente con fichas de dominó comenzando a partir del cuadro adyacente a c1. Siendo par el número de cuadros se puede hacer así. Supongamos que el camino par sea el último señalado. Ahora escogemos el camino serpenteante síguiente:
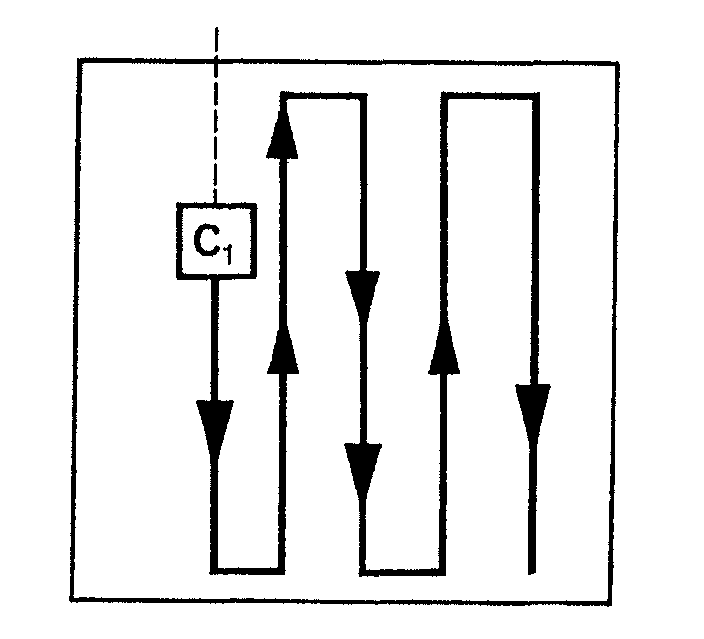
Comenzamos a cubrirlo con fichas a partir de c1 en la dirección señalada. En el camino está c2, pero, por razón de la diferencia de color, llegamos exactamente cubriendo con nuestras fichas hasta el cuadro adyacente a c2. Luego nos saltamos c2 y llegamos cubriendo al fin de nuestro camino sin problemas. La razón que está debajo de esta receta es clara. Fíjate que desde c1 hasta c2 por el camino que llevas hay un número par de cuadros y así desde c2 hasta la esquina final también.
La receta de Gomory es la siguiente. Nos pensamos el tablero cubierto con los dos tenedores de Gomory que aquí te señalo (líneas gruesas serpenteantes):
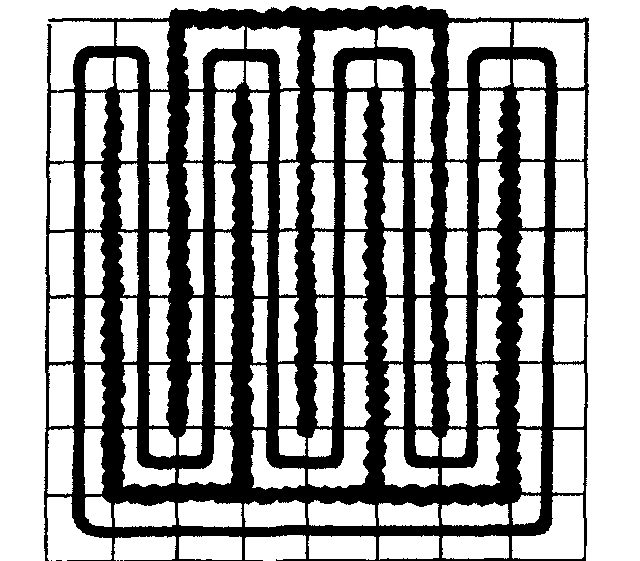
Lo que hacen los dos tenedores es delimitar el camino cerrado indicado en la figura que recorre todos los cuadros una sola vez cada uno. Si se tapa un cuadro blanco y otro negro en cualquier sitio, se puede rellenar con fichas el camino entre ellos por las dos direcciones posibles, pues hay un número par de cuadros en cualquiera de ellas. Ingenioso, ¿no?
¿Qué otros problemas
del mismo sabor se pueden proponer? Por ejemplo, en un tablero 9 X 9 se
quitan uno o tres cuadros. ¿Se podrá rellenar con fichas
de dominó? ¿Cómo?
NOTAS
El ajedrez sugiere multitud de problemas y juegos muy variados. Uno de ellos, interesante y muy antiguo, que permite un tratamiento matemático completo es el de las ocho reinas. ¿Puedes colocar ocho reinas sobre el tablero sin que ninguna pueda comer a ninguna otra? Más general, en un tablero n X n, ¿cuál es el número máximo de reinas que se pueden colocar sin que ninguna amenace a ninguna otra? ¿Cuántas posibilidades diferentes hay de colocarlas con esta condición? Un juego interesante para dos jugadores A y B, basado en este problema es el siguiente: A coloca una reina en el tablero, luego B coloca otra de tal modo que no esté amenazada por la primera, luego debe colocar A otra que no esté amenazada por ninguna de las anteriores... Pierde quien no pueda colocar una reina sin ser amenazada.
Otro juego también antiguo es el del paseo del caballo. ¿Podrías señalar un paseo de un caballo por todos los cuadros del tablero sin que pase dos veces por un mismo cuadro? ¿Puedes hacerlo saliendo de un cuadro cualquiera? ¿Y en un tablero cualquiera nxn o bien nxm?