Las matemáticas de un bocata

¿Qué figura tiene tu loncha? Se parece a una elipse, ¿no? ¿Será una elipse? ¿Qué has hecho tú para que sea una elipse? ¿Qué cosa es una elipse? Recuerda: una elipse es un conjunto del plano formado por todos los puntos cuya suma de distancias a dos puntos fijos, los focos, es constante. Parecería milagro que tú, que lo único que querías era cortarte una buena loncha de chorizo, te hayas trazado una elipse. Parece que habría que andarse con muchísimo cuidado para que la loncha salga con una figura así. Y, sin embargo, ahí tienes una elipse.

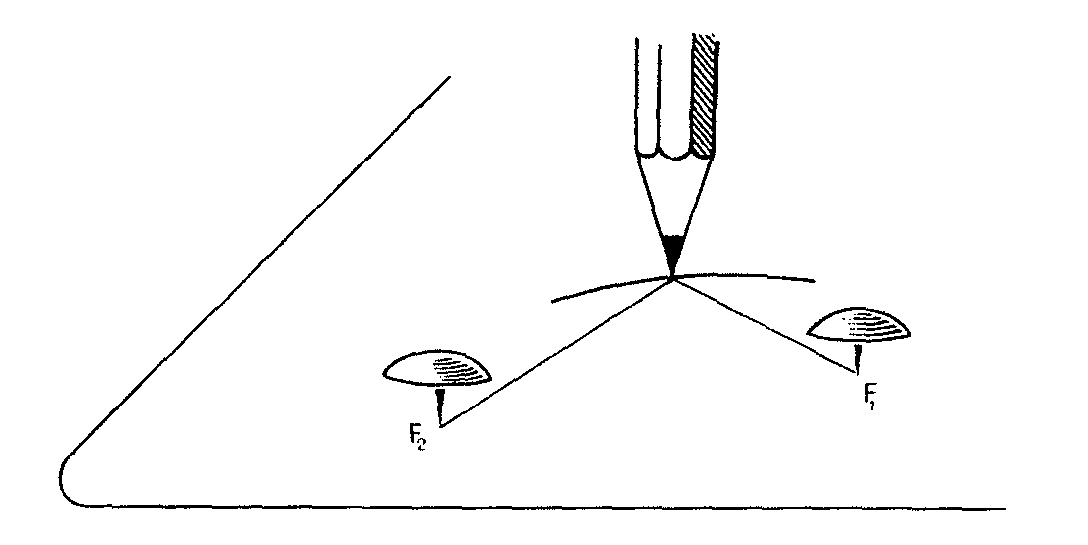
Para verlo bien, imagina el momento cuando el chorizo estaba aún entero, hace casi nada, y en él imagina el corte que le has dado ahora. Imagínate que, tangentes a tu cuchillo, a un lado y a otro, y tangentes a la pared del chorizo por dentro, has colocado, ¡a quién se le ocurre!, dos pelotas de píng-pong que da la casualidad de que encajan perfectamente. Así:
 
 

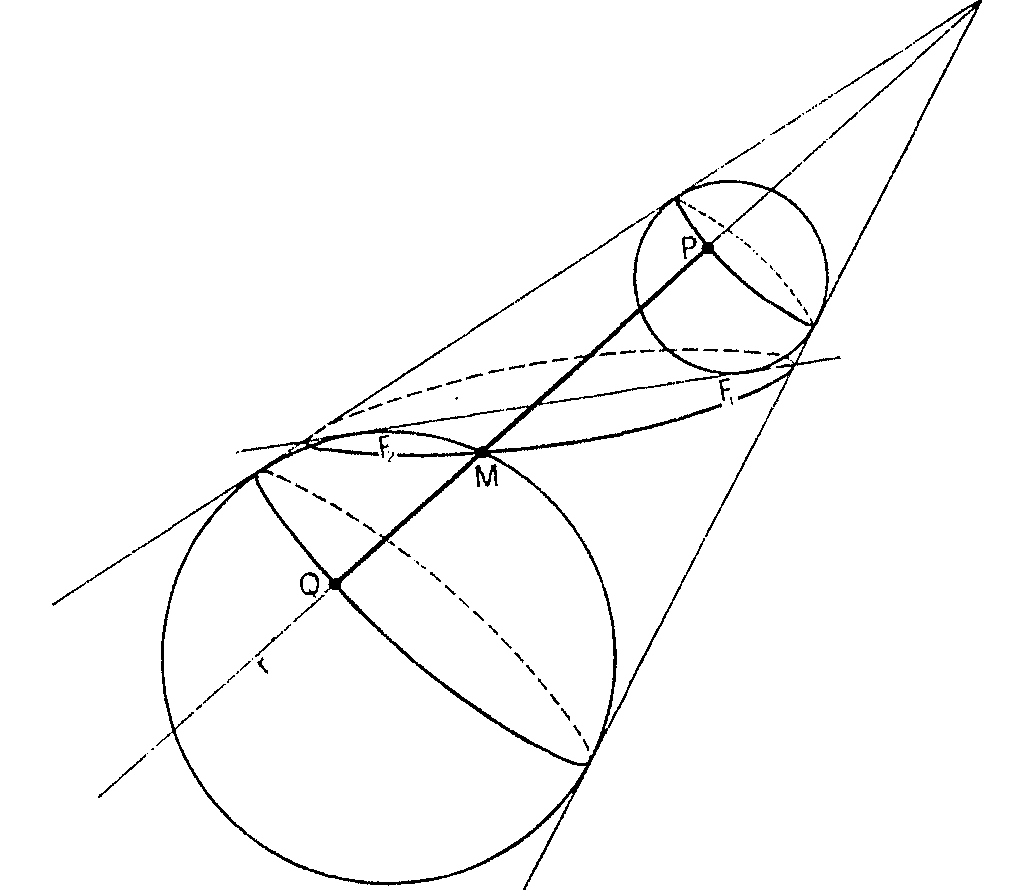
Ahora considera los puntos F1 y F2 en que las pelotas de píng-pong son tangentes al corte y observa lo que pasa con un punto cualquiera del borde del corte. Traza por él la recta paralela al eje del chorizo. Esta recta será tangente a las pelotas de ping-pong en P y Q. Por otra parte, MF1 es tangente a la pelota de la derecha y MF2 a la de la izquierda. Si desde un punto exterior a una pelota trazas dos tangentes cualesquiera a ella, los segmentos determinados por el punto y los puntos de tangencia tienen la misma longitud.

Así resulta aquí, MF1 = MP, MF2 = MQ, MF1 + MF2 = MP + MQ = PQ = constante, porque PQ es la misma longitud para cualquier r que podamos trazar en la superficie del chorizo paralela al eje. Así, el punto M recorre una elipse de focos F1 y F2.

De modo que una elipse es muy fácil de trazar. Se toma una loncha de chorizo, se coloca encima de un papel y el borde del manchurrón que queda en él es una elipse. Si la quieres menos grasienta puedes usar el tubo de cartón que va dentro de un rollo de papel higiénico o de papel de cocina, lo cortas oblicuamente con un cuchillo, colocas el borde sobre un papel y lo trazas con un lápiz.

Uno diría que la elipse, tal como se enuncia, «el lugar geométrico de los puntos del plano tales que ... », sería una pura invención de los matemáticos. Y, sin embargo, no es así. Elipses aparecen hasta en la sopa sin ser llamadas. Inclina un poco la cazuela en que la sopa está. El borde de la superficie es una elipse. ¿Tienes por ahí un flexo? Enciéndelo, ponlo encima de la mesa y vete mirando la forma que tiene la zona iluminada de la mesa cuando inclinas el flexo. ¿No te recuerda la de la loncha de chorizo? ¿Será también una elipse? ¡Claro que sí, y por la misma razón! Observa. La zona de luz es, más o menos, la de un cono de base circular.
 
 

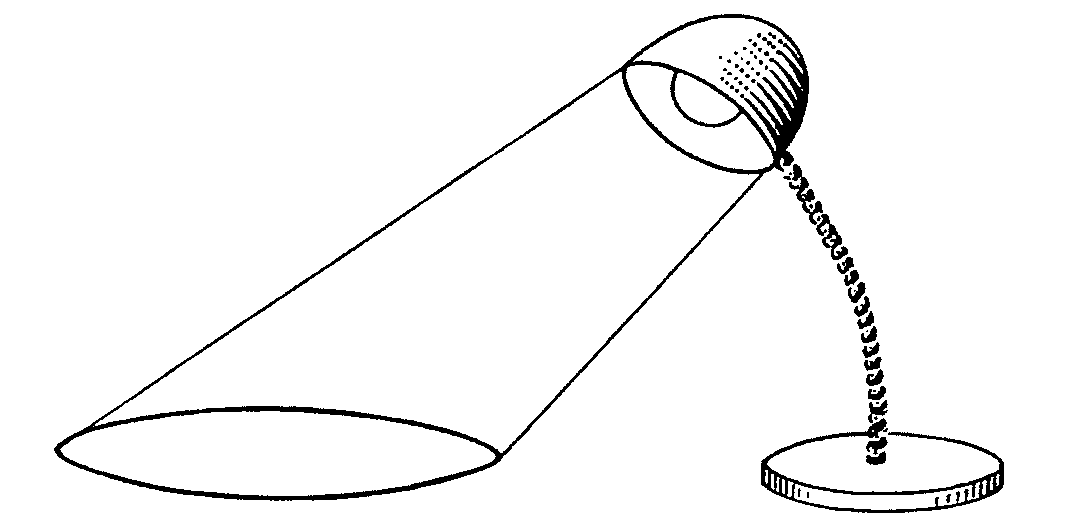
Cortar la zona iluminada por la mesa es como cortar un enorme chorizo cónico con la mesa. ¡Qué idea! Vamos a usar el mismo truco que antes para ver si la figura es una elipse. ¿por qué no? Colocamos dos pelotas, ahora serán de tamaño diferente, tangentes al cono y al plano de la mesa a uno y otro lado de ésta, como te indico en la figura. Como antes, resulta MP = MF1, MQ = MF2, y así MF1 + MF2 = MP + MQ = PQ = constante independiente de r. Por tanto, M describe una elipse de focos F1, F2.

La elipse surge de manera realmente inesperada en muchas otras ocasiones, como la siguiente. Tienes una escalera de mano apoyada en la pared. Estás subiendo por ella. Aún no has llegado arriba.

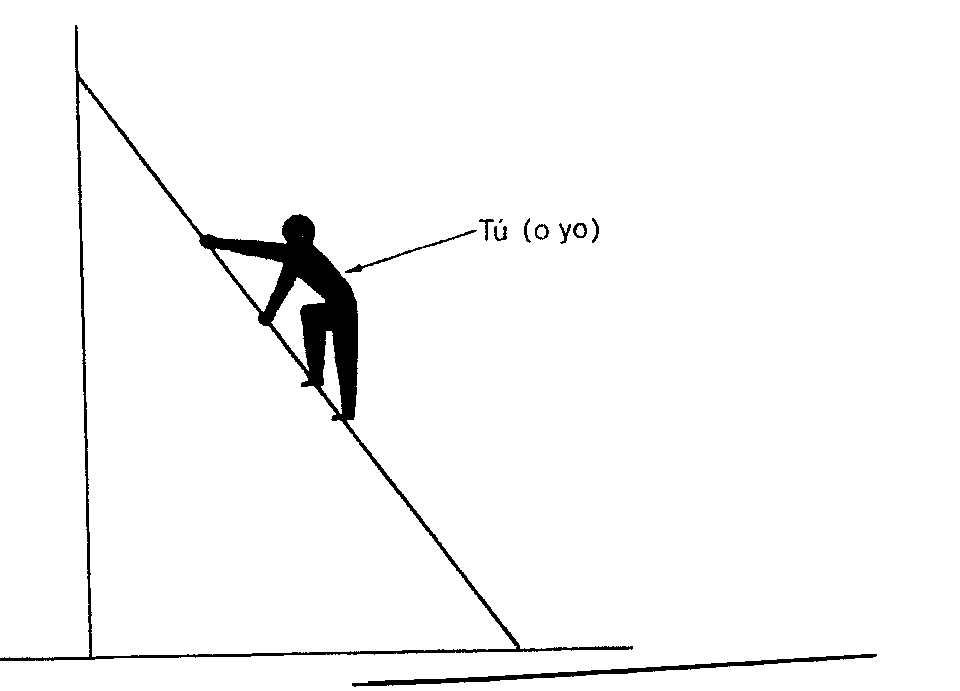
De repente, joh fatalidad!, empieza a resbalar. Cuando el resbalón acaba con tu golpazo en el suelo, probablemente no se te haya ocurrido pensarlo, pero, ¿sabías que tu pie, por ejemplo, ha trazado limpiamente un trozo de elipse en el aire? ¡Fíjate! La suma de distancias de tu pie a dos puntos fijos ha sido constante todo el tiempo de tu caída (suponiendo, claro, que no has pegado un brinco extraño en el aire al apercibirte de lo que te iba a suceder, lo cual, por otra parte, sería lo más acertado). ¡Quién lo diría!

Con un poco de geometría analítica que sepas lo puedes ver fácilmente.

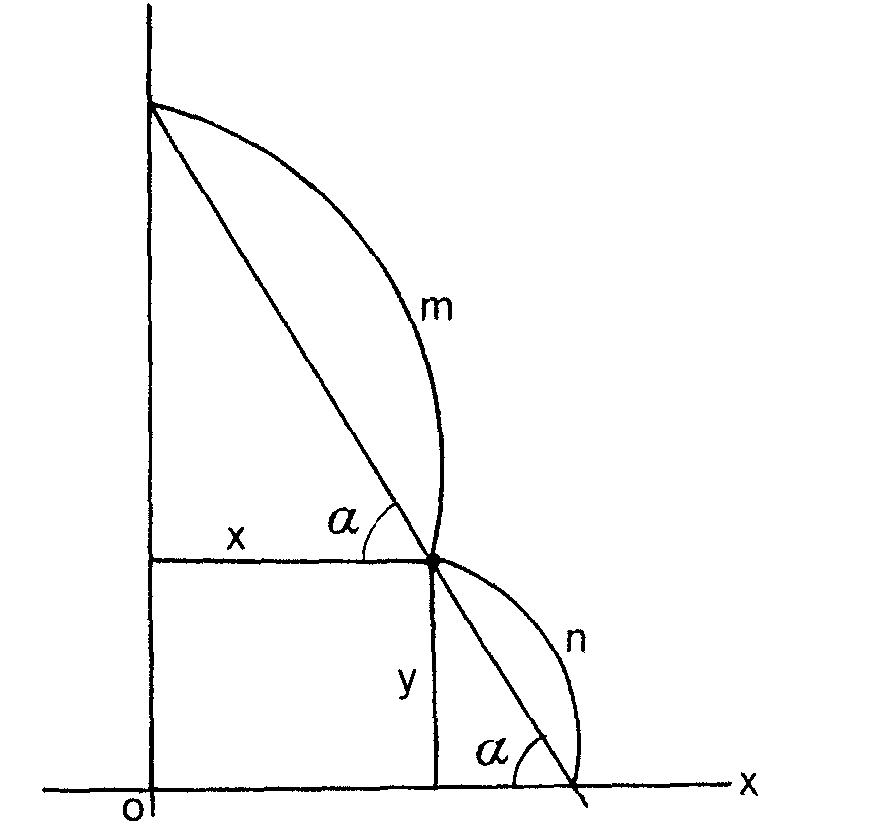
Suponte que tu pie está en el punto gordo indicado de la escalera que va cayendo (m y n, fijos; el ángulo a achicándose). Se trata de ver cuál es la curva que describe ese punto gordo de la escalera. Sus coordenadas: x = m cos a, y = n sen a

Es decir, la suma de distancias del punto a F1 y F2 es constante, 2m. Esto es el eje mayor de la elipse. Así, el semieje mayor de la elipse es precisamentelo que te faltaba para llegar al final de la escalera. El semieje menor es la distancia de la escalera que tenías recorrida cuando ésta empezó a resbalar, n.

Aquí tienes una forma sencilla de hacer surgir una elipse a partir de su definición. Toma un hilo, fija cada extremo con una chincheta a un punto en una cuartilla de modo que sobre algo de hilo. Ahora toma un lápiz, con su punta tensa el hilo y con el hilo tenso deja resbalar el lápiz. La figura es claramente una elipse, pues en todo momento la suma de distancias del punto que trazas a las dos chinchetas, los focos, es fija e igual a la longitud del hilo.

Una forma más inesperada de obtener una elipse es la siguiente. Toma un papel. Con un compás traza una circunferencia. Recorta el circulo. Señala un punto cualquiera P, dentro del círculo, que no sea su centro. Ahora toma el papel y pliégalo de modo que al plegarlo resulte que el borde del círculo vaya a pasar por P. Despliega y pliega otra vez de modo que se cumpla la misma condición. Haz muchos pliegues semejantes. Al final, encontrarás que todos los pliegues envuelven una figura que se parece a una elipse. ¿Será una elipse?

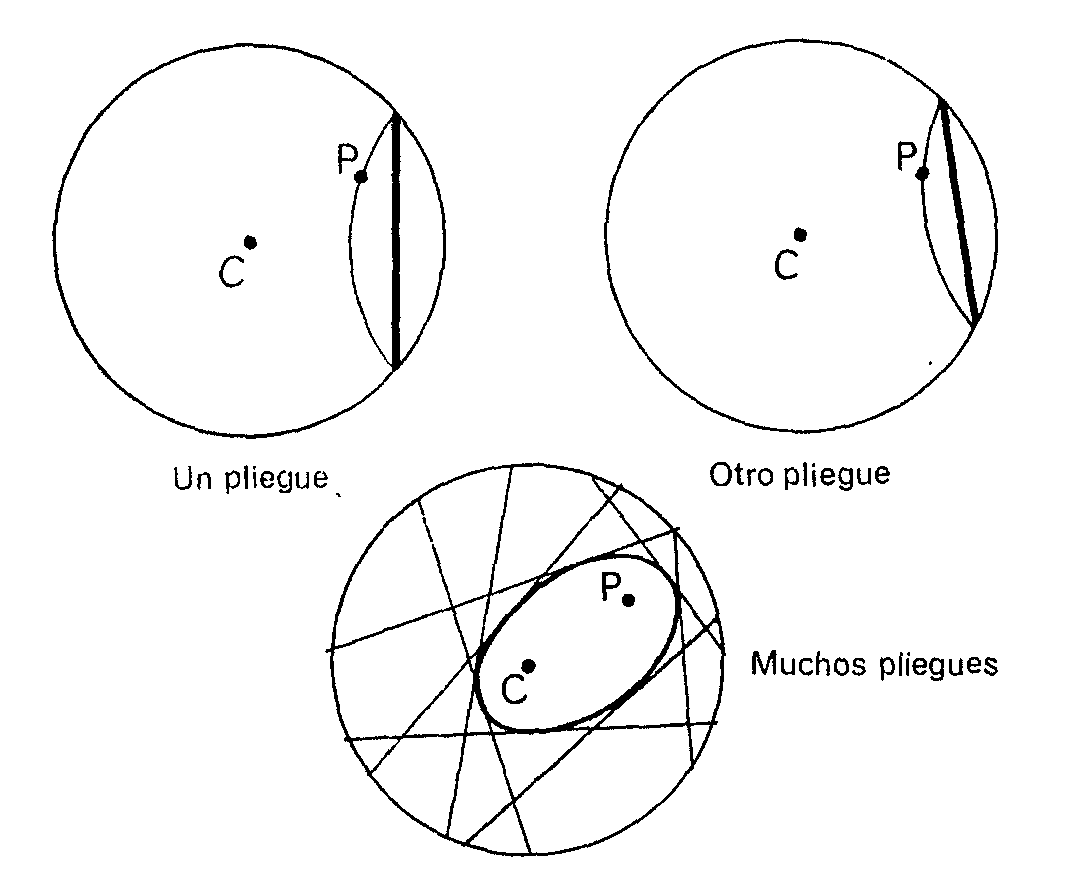
¡Sí! Y verás que no es difícil demostrarlo. Considera un pliegue cualquiera como el de la figura siguiente.

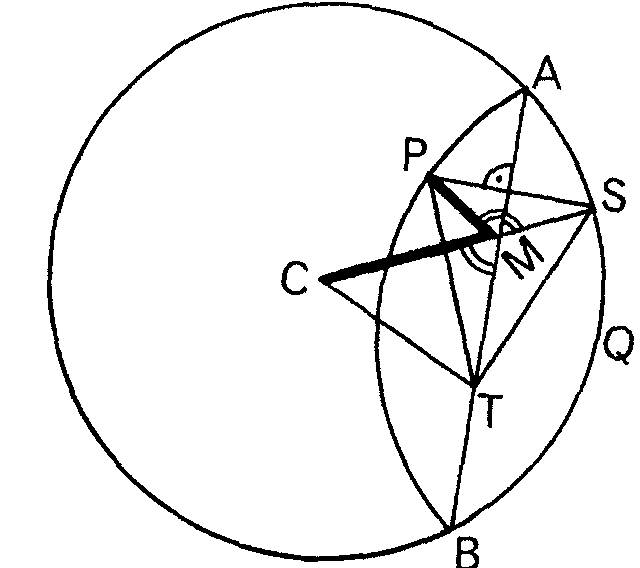
El arco que pasa por P es simétrico del arco AQB con respecto al pliegue. Traza la perpendicular por P a AB, al pliegue. AB es mediatriz de PS. Une C a S que corta en M a AB. Resulta entonces MP = =MS y así MC +MP=MC+MS= radio del círculo. Así resulta que M está sobre una elipse de focos C y P con eje mayor de longitud igual al radio del círculo. Además, para otro punto cualquiera T de AB se tiene TP + TC = TS + TC > CS (pues el lado CS del triángulo TSC es menor que la suma de los otros dos). Así, T no está en la elipse. Es decir, el único punto de AB sobre la elipse es M, en otras palabras, AB es tangente a la elipse en M. Esto explica que los pliegues envuelven a la elipse.

Además, mira la figura y verás que, por la simetría, el ángulo PMA es igual al AMS y éste es igual al CMB, es decir, que resulta que la tangente AB a la elipse con punto de tangencia M es la bisectriz exterior del ángulo que tiene M por vértice y lados las semirrectas que van de M a los focos de la elipse. Recuerda bien este hecho porque nos resultará muy interesante un poco más adelante.

Esta otra propiedad, que puedes deducir mirando fijamente a la misma figura anterior, es también muy curiosa. La proyección de P sobre las tangentes a la elipse recorre una circunferencia, homotética de la de partida con centro de homotecia P y razón de homotecia 1/2.

Unas cuantas preguntas para que te las pienses. ¿Te podrías inventar un método como el de las chinchetas para trazar una parábola o una hipérbola?

En el método de los pliegues, ¿qué podrías hacer para obtener de modo semejante, con pliegues, una hipérbola?

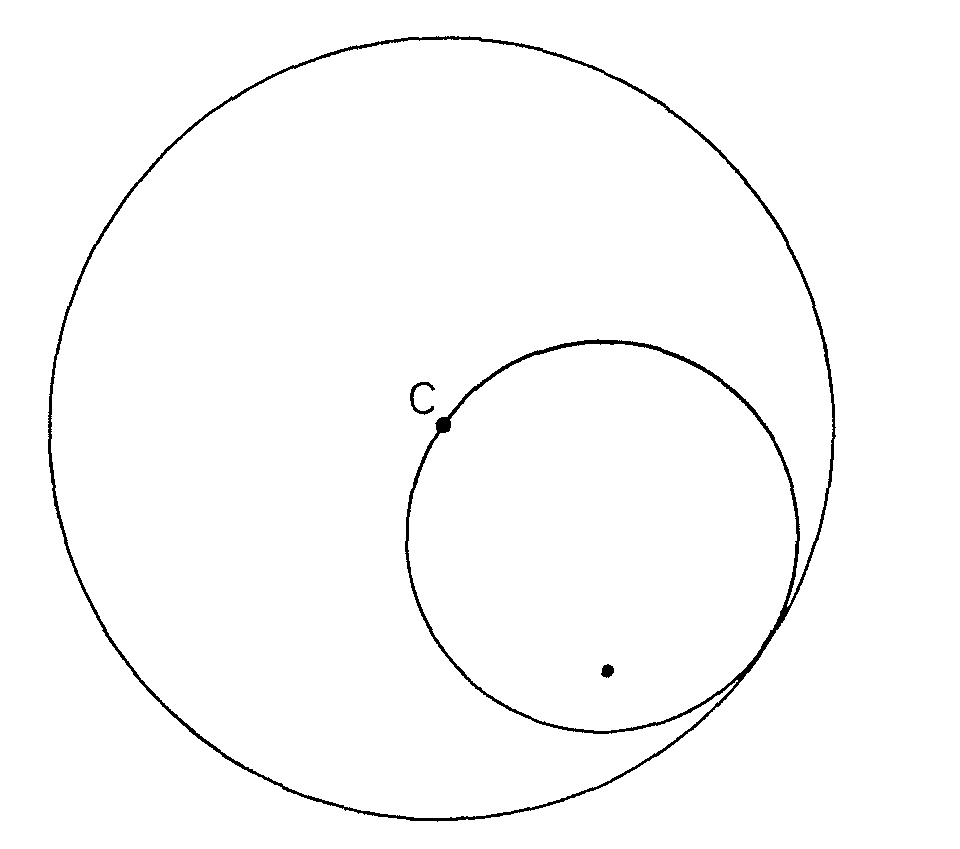
Para acabar esta merienda de elipses, que comenzó con un bocata de chorizo, voy a ofrecerte un postre nada despreciable. Mira a ver si encuentras una caja circular como esas metálicas de galletas caras. Mide el diámetro de su interior, dibuja y recorta en una cartulina un círculo de diámetro igual al radio del interior de la caja. Pega en el fondo de la caja un papel o cartulina sobre la que va a aparecer el milagro de la elipse. Ahora se trata de colocar el círculo pequeño sobre el fondo así recubierto de la caja pegado a su pared y de hacerlo mover con su borde pegado a la pared interior de la caja sin deslizarse, es decir, se trata de que ruede sin resbalar. Para esto, lo mejor es recubrir la pared interior de la caja, por ejemplo con una tira de ese papel engomado por las dos caras que se usa para pegar alfombras al suelo. Haz un agujero en un punto de tu círculo pequeño, del que rueda, mete ahí la punta de un lápiz y verás que, al moverse como hemos quedado, sin resbalar, el lápiz describe sobre el papel del fondo algo que se parece a una elipse. ¿Es una elipse? A ti te lo dejo para que lo compruebes.

NOTAS

La geometría de las cónicas, elipse, hipérbola y parábola, es una de las secciones profundas de la matemática que, por su belleza, armonía y riqueza de ideas, se ha desarrollado más precozmente.

Los tres grandes genios de la matemática griega, Euclides, Arquímedes y Apolonio son los responsables de que ya a finales del siglo III a. de C. se conociese prácticamente tanto como hoy conocemos sobre las propiedades de las cónicas.

Toda esta evolución tuvo lugar alrededor del gran centro de estudios de Alejandría, en Egipto, la ciudad fundada en 322 a. de C. por Alejandro Magno y que sirvió por más de 5 siglos, hasta mediados del siglo 3 d. de C., como el centro cultural más importante de la humanidad, con su gran museo, su biblioteca de más de 500.000 volúmenes y sus escuelas de las diferentes ramas del saber. La de matemáticas fue fundada por Euclides hacia 300 a. de C. en tiempo de Tolomeo I. De la vida de Euclides no se sabe más que algunas anécdotas curiosas. Un alumno le interrumpió una vez su explicación sobre geometría preguntándole qué se podría ganar con aquellas elucubraciones tan extrañas. Euclides se dirigió a su esclavo allí presente: «Dale una moneda y que se vaya. Es de los que sólo quieren saber para ganar». La obra principal de Euclides, los Elementos, ha sido una de las más influyentes en el pensamiento de la humanidad. Se ha venido usando como libro de texto en todos los países hasta bien avanzado el siglo 19. Se dice que sólo la Biblia le sobrepasa en número de ediciones. Su importancia radica en que ha sido el modelo de método de pensamiento en el que las generaciones del mundo occidental se han formado por más de 22 siglos.
Arquímedes (287-212) es considerado como el matemático más genial de la Antigüedad. Nació en Siracusa (Sicilia), colonia griega. Era hijo de Fidias, astrónomo, emparentado de alguna forma con el rey Herón II de Siracusa. Arquímedes estudió en Alejandría, asimiló y perfeccionó los métodos de los discípulos de Euclides y se volvió a Siracusa, desde donde sorprendió al mundo con sus descubrimientos e invenciones, entre otros muchos, el de su famoso principio «Todo cuerpo sumergido en un líquido ... ». Éste está relacionado con la clarificación por Arquímedes de la estafa que un orfebre había hecho al rey Herón. Éste le había encargado una corona de oro confiándole para ello un determinado peso de oro puro. El rey sospechaba que el orfebre había quitado una cierta cantidad de oro y lo había sustituido por una cantidad de plata del mismo peso. Arquímedes, en una de las piscinas públicas de la ciudad, meditaba sobre el modo de averiguar si esto era así. De pronto, al sentir su cuerpo flotando en el agua, un relámpago cruzó su mente. Una cantidad de oro de un cierto peso tiene un volumen menor que una cantidad de plata del mismo peso. Por tanto, si la corona tiene plata como el rey sospecha, tendrá un volumen mayor que el oro que el rey entregó al orfebre. Basta meter en agua la corona, medir el agua desalojada, meter en agua una cantidad de oro con el mismo peso que la corona, medir el agua desalojada, y comparar. Arquímedes no pudo contenerse. Salió del baño desnudo por las calles de Siracusa gritando «¡Eureka, eureka!» (¡Lo encontré, lo encontré!).

Y sin embargo, a pesar de todas sus famosas invenciones (palanca, espejos parabólicos para quemarles las naves a distancia a los romanos que asediaban Siracusa, una especie de gigantesco tornillo para subir cómodamente el agua de un pozo ... ) lo que Arquímedes estimaba más eran sus descubrimientos geométricos. En su tumba hizo grabar una esfera inscrita en un cilindro, en recuerdo de su descubrimiento de que el volumen de la esfera es 2/3 del volumen del cilindro.

Pero quien más supo sobre cónicas fue Apolonio de Perga. Nació hacia 262 a. de C. en Perga, una ciudad griega situada en la actual Turquía. Estudió y enseñó también en Alejandría, donde murió en 190 a. de C. Se ocupó también de óptica y astronomía, introduciendo métodos muy originales y obteniendo resultados muy profundos.