Algunos piensan que el computador es idiota. Hace falta contarle completamente el chiste y explícárselo bien para que se ría. Una coma en lugar de un punto y coma y ya se ha liado. La verdad es que también el boli es aún más imbécil y sin su ayuda pocos problemas seríamos capaces de resolver.
La historia que te voy a contar es la de un problema que sólo muy recientemente se ha podido resolver, y con la ayuda indispensable de un computador. Y eso que no se trata tan sólo de contar rápido. Probablemente son muchos los resultados matemáticos profundamente dormidos en los circuitos de nuestros computadores esperando el programa de nieve que sepa arrancarlos.
En 1950 se sabía que cualquier mapa de menos de 36 países se puede colorear con cuatro colores. En los años cincuenta, Heinrich Heesch, profesor en Hannover, empezó a pensar que las ideas de Kempe, junto con la ayuda del computador, podrían tal vez conducir a una solución, pero, aunque presentía cómo se podría hacer la cosa, aún estaba lejos de la realización de su plan de trabajo. Desde 1950 a 1970 Heesch fue desarrollando las técnicas que han conducido a la solución. El perfeccionamiento y realización de este plan de trabajo ha sido llevado a cabo, desde 1970 a 1976, por Kenneth Appel y Wolfgang Haken, de la Universidad de Illinois. Después de muchas horas de pensar y de trabajo y diálogo con el computador, por fin pudieron anunciar, en junio de 1976, que, efectivamente, cuatro colores bastan.
Intentaré darte una idea de los puntos que han marcado el camino hacía la extraña forma de solución que ahora tenemos.

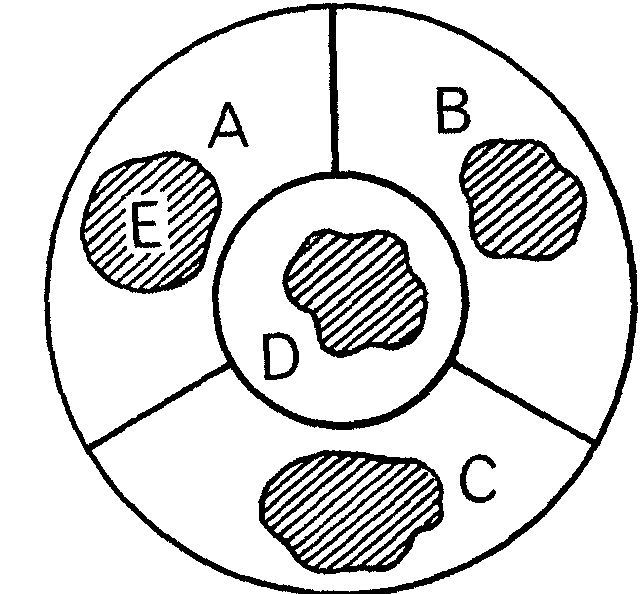
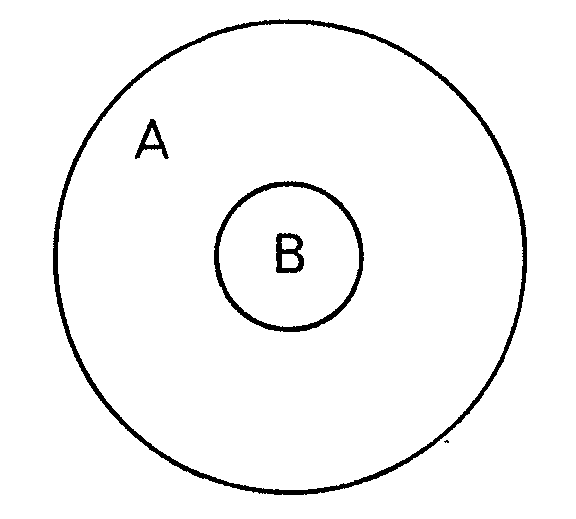
En este mapa en el que E es el país
rayado, con enclaves en todos los otros, se necesitan cinco colores.
También es claro que tres colores
no bastan para colorear cualquier mapa. Éste, por ejemplo,
 |
necesita cuatro.
Heawood demostró muy pronto que 5 colores bastan. ¿Bastarán cuatro?
Para algunos de los razonamientos que vamos a utilizar, es conveniente poner el problema en otra forma más cómoda equivalente a la que tenemos. Para un mapa cualquiera podemos señalar un grafo asociado de la siguiente manera. (Grafo, recuerda, es simplemente un conjunto de puntos, vértices, unidos algunos de ellos por unas cuantas líneas, arcos). Lo hacemos de la siguiente forma. En el interior de cada país señalamos una capital. Las capitales van a ser los vértices del grafo asociado, grafo dual. Si dos países tienen línea de frontera común, unimos sus capitales por una carretera que cruce la línea de frontera común sin que estas carreteras se crucen. Tales carreteras serán los arcos del grafo dual.
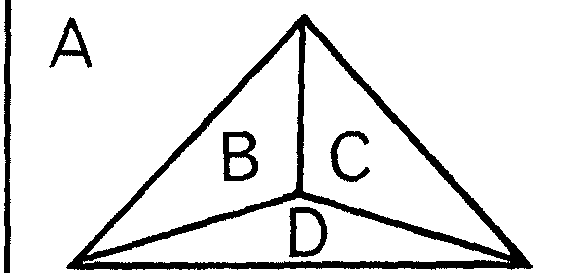
Por ejemplo, si el mapa es éste
señalamos las capitales y las unimos según la regla señalada:
Resulta así el grafo dual
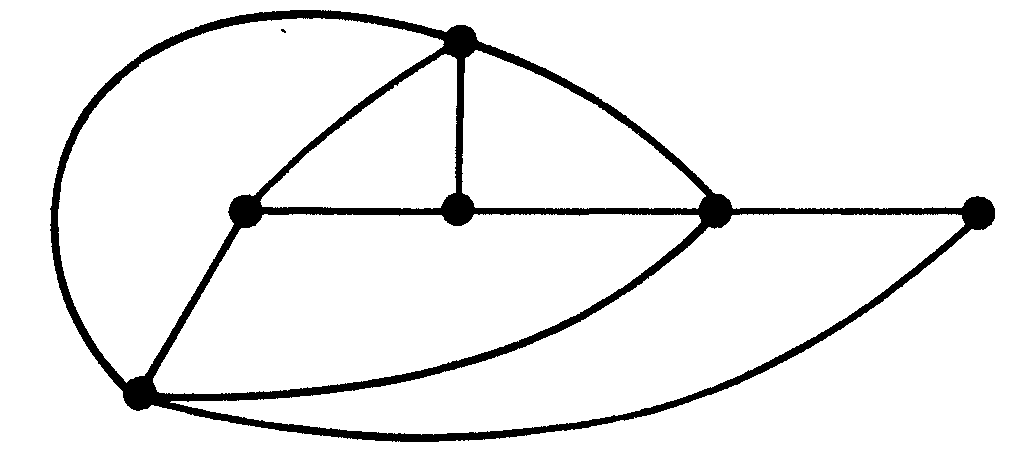 |
El grado de un vértice (capital) del grafo dual, es decir, el número de arcos concurrentes en él, es el número de países vecinos del país correspondiente a esa capital (vértice).
El problema, en términos del grafo dual, consiste en determinar el número mínimo de colores para colorear un grafo como el que resulta de un mapa de la forma dicha de modo que dos vértices adyacentes tengan distinto color.
La demostración que Kempe dió en 1879 de que cuatro colores bastan es ciertamente ingeniosa y, aunque falsa en un punto, ha sido su esquema el que se ha utilizado en la demostración que hoy tenemos. Por eso vale la pena conocerla. Con ello será fácil entender el camino actual hacia el teorema.
La «demostración» de Kempe
Llamemos mapa penta (pentacromático, si no quieres abreviar) a un mapa que exija cinco colores para ser bien coloreado. No se puede colorear con menos.
Nuestro objetivo es demostrar que no existe ningún mapa penta.
Llamaremos mapa normal a aquel que verifica las dos condiciones siguientes: a) no contiene un país aislado dentro de otro, es decir, un país con un solo vecino; b) ningún punto de frontera es frontera de más de tres países vecinos.
Se excluyen, por tanto, situaciones como las siguientes:
Observa que el grafo asociado a un mapa normal (los puntos de frontera son frontera de dos o tres países a lo sumo) es una triangulación curvilínea del globo, es decir, una partición del globo en triángulos curvilíneos.
Ahora podemos entender la demostración de Kempe de que no existe mapa penta en los cuatro pasos siguientes:
1) Si existe mapa penta M, existe mapa penta normal.
En efecto, si M tiene configuraciones parciales así:
se sustituyen por otras así:
y si tiene alguna configuración parcial de este tipo (algún punto de frontera de más de tres países)
se sustituye por otra así (mediante la adición de un país resulta que ningún punto de frontera es frontera de más de tres países vecinos):
Llamemos M* al nuevo mapa, claramente normal. Si el nuevo mapa M* no fuese penta, lo podríamos colorear con cuatro colores. Lo coloreamos. Pero entonces, añadiendo los países que a M le hemos quitado para obtener M* y suprimiendo los que hemos añadido, fácilmente resulta que M también es coloreable con cuatro colores, en contra de lo que habíamos supuesto.
2) Si existe mapa penta normal, existe mapa penta normal y mínimo, es decir, con el menor número posible de países. Consideramos todos los mapas penta normales. Cada uno tiene un número finito de países. Alguno habrá con el menor número. Clarísimo, ¿no?
3) Cualquier mapa normal contiene al menos un país con menos de seis países vecinos.
Esto se pone más serio y empieza a ser más profundo. También este paso de Kempe va a ser totalmente válído.
Para entender mejor este paso, consideramos el mapa normal, que sabemos que es una partición de la esfera en polígonos curvilíneos. Le podemos aplicar el teorema de Euler que ya conoces:
Por otra parte, cada arco o arista es frontera de dos países vecinos, y así,
2C2 + 3C3 + 4C4 +...
es el número de arcos contados dos veces, es decir,
2A =2C2 + 3C3 + 4C4 +...
Por otra parte, el mapa es normal y así en cada vértice concurren exactamente tres arcos de frontera. Por eso 3V es también el número de aristas contadas dos veces, es decir,
C = C2 + C3 + C4 +...
2A =2C2 + 3C3 + 4C4 +...
2A = 3V
C+V=A+2
resulta fácilmente
12 = (6 - 2) C2+(6-3) C3+(6-4) C4+
(6-5) C5 + (6-6) C6+ (6-7) C7 + ...
Por tanto, como la suma es 12, alguno de los números C2, C3, C4, C5es mayor que cero, que expresa precisamente lo que tratamos de demostrar. Ingenioso, ¿no? Esta relación de Kempe ha dado mucho juego en la demostración que se ha logrado en 1976.
4) Ningún mapa penta normal y mínimo puede contener un país con menos de seis países vecinos
Si lográramos demostrar esto ya tendríamos que no puede existir mapa penta, puesto que esto contradice 3), que ya lo tenemos establecido. En este punto se equivocó Kempe, pero al final del todo. Una buena parte de su razonamiento es también válida y ha servido para la demostración correcta.
Para demostrar 4) empezamos considerando un mapa M penta normal y mínimo. Si contuviese esta configuración parcial
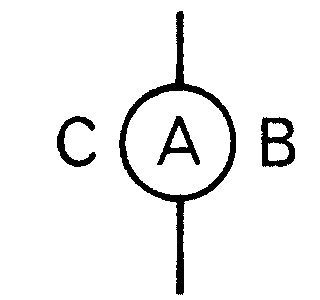
país A con dos vecinos, el mapa M* que resulta al sustituir en M dicha configuración parcial por esta (supresión de A)
es normal y no es penta, pues tiene un país menos que M, y M era penta normal y mínimo. Así, M* se puede colorear con cuatro colores. Lo coloreamos. Pero ahora es claro que M también se puede colorear con cuatro colores, restituyendo A y dándole un color distinto del de B y C. Esta contradicción demuestra que M no puede tener la configuración supuesta, si es que existe.
La configuración siguiente (A con tres vecinos)
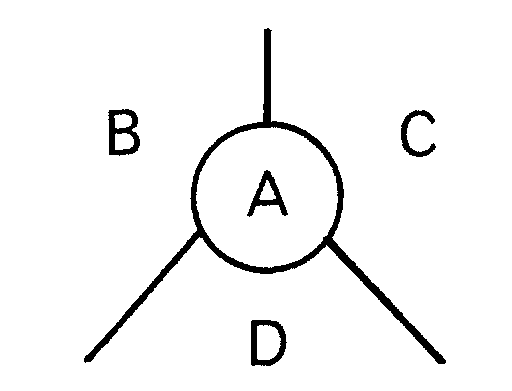
se excluye de la misma forma, suprimiendo A, coloreando el mapa M* que resulta y luego coloreando el M.
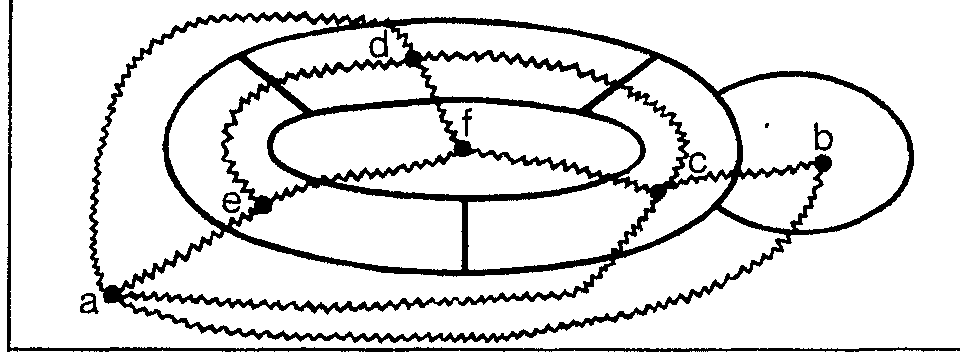
La exclusión de la configuración
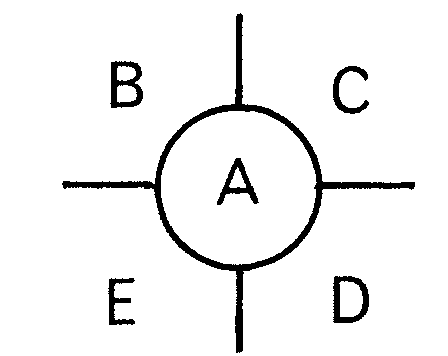
es más complicada. Pasamos al grafo dual para razonar más cómodamente. El grafo dual es una triangulación de la esfera que contiene la configuración parcial
Eliminamos el país a identificando a con b y queda así esta configuración reducida:
El grafo resultante no es penta. Se puede colorear con cuatro colores, 1, 2, 3, 4. Distinguimos dos casos.
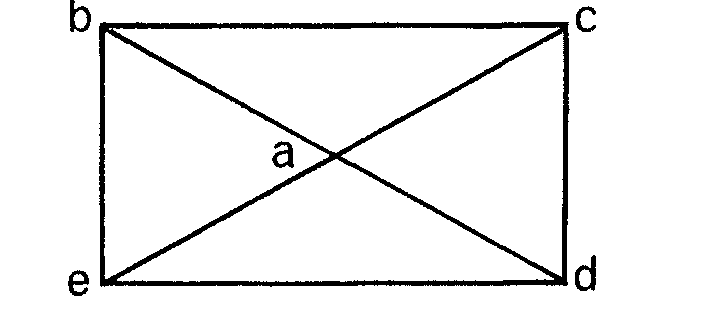
Caso 1. Si c y e tienen el mismo color, 2 por ejemplo, entonces b tendrá otro, el 3 por ejemplo, y d otro distinto, el 4 por ejemplo. Así:
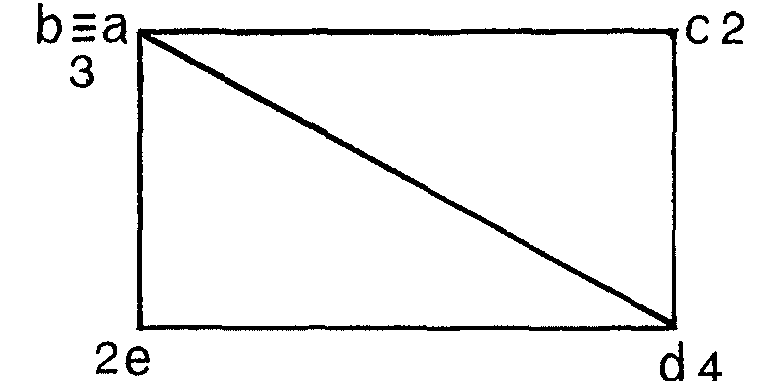
Entonces restituimos a, le damos el color 1 y resulta el grafo inicial coloreado con cuatro colores, contra la suposición de que era penta.
Caso 2. Si c y e tienen distinto color, 2 y 3 por ejemplo, entonces b y d tienen el 1 y el 4, como se indica:
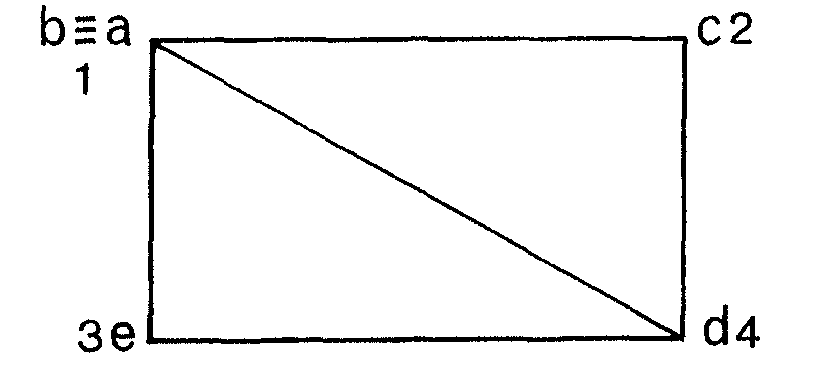
Entonces, o bien se puede ir de c a e por arcos fuera del rectángulo bcde pasando por una cadena de vértices 232323 ... 23 (cadena de Kenipe) o no se puede. Si se puede, entonces es que no se puede ir por fuera del rectángulo desde b a d por una cadena 141414 ... 14. Tomamos el par bd o ce para el que no se puede. Sea ce, por ejemplo. Partiendo de c hay un tramo 2323... que no se puede continuar por tropezar con la cadena 141414...14 de b a d. Ese tramo se cambia a 3232... y así nos colocamos en el caso 1 y podemos proceder como allí.
El fallo de Kempe estuvo en la reducción que quiso hacer de la configuración
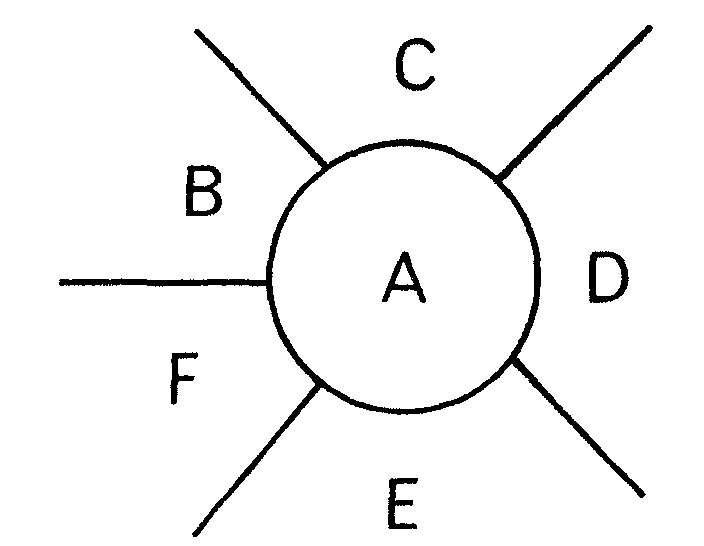
de un modo semejante, pero más complicado. Su demostración fue falsa aquí. Pero con lo que hemos visto ya está bien clara la idea. Te la escribo de nuevo en términos modernos, esta vez en tres pasos.
La demostración de Appel y Haken
A la vista del esquema de la demostración de Kempe, entenderás el esquema siguiente.
1) Todo mapa penta normal tiene
ciertos conjuntos inevitables de configuraciones. El conjunto inevitable
de configuraciones parciales de Kempe fue éste:
 |
| Conjunto
inevitable de configuraciones, es decir, alguna de las configuraciones
de este conjunto tiene que estar en el mapa.
2) Hay ciertas configuraciones que no pueden entrar en un mapa penta mínimo (configuraciones reducibles). Kempe demostró que las configuraciones parciales |
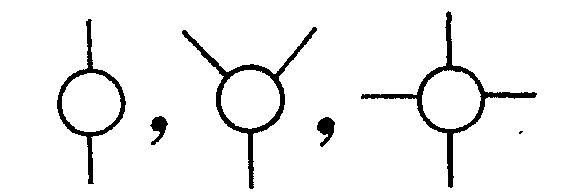 |
| son reducibles. La demostración que dió para |
 |
| fue falsa. |
3) La construcción de un conjunto inevitable de configuraciones cada una reducible implica la no existencia de un mapa penta.
En junio de 1976 Appel y Haken lograron
construir un conjunto de 1482 configuraciones cada una reducible.
En los últimos treinta años los aficionados al problema, especialmente Heesch, lograron idear métodos programables en el computador para construir conjuntos inevitables de configuraciones. También se hicieron programas para comprobar si una configuración es reducible o no. Estos programas eran complicados y largos; tanto, que incluso los computadores modernos necesitarían siglos para comprobar si las configuraciones de ciertos conjuntos inevitables que había que considerar eran reducibles o no. Appel y Haken lograron reducir la tarea a unas dimensiones más manejables. Con ello lograron finalmente en 1976 obtener el resultado. El problema estaba resuelto.
El método consistió en un diálogo inteligente con el computador. Es interesante oírles a ellos describir cómo en cierto momento de su trabajo el computador comenzó a enseñar a sus maestros el modo adecuado de proceder,
«En este punto, el programa, que para entonces había absorbido nuestras ideas y mejoras de dos años, comenzó a sorprendernos. Al principio comprobábamos sus razonamientos a mano de modo que podíamos siempre predecir el curso que seguiría en cualquier situación dada, pero ahora comenzó de repente a actuar como una máquina de jugar al ajedrez. Se fabricaba estrategias compuestas basadas en los trucos que se le habían «enseñado» y a menudo estos ensayos eran mucho más inteligentes que los que nosotros habríamos intentado. Así comenzó a enseñarnos cosas acerca del modo de proceder que nosotros nunca hubiéramos esperado. En cierto sentido había sobrepasado a sus creadores en algunos aspectos de la tarea «intelectual» así como lo había hecho en las partes mecánicas de la tarea.»
Después de oír
esto te puedes volver a preguntar: ¿Es el computador tonto o listo?
Un computador bien enseñado te gana al ajedrez, te gana al Nim,
te gana al Tres en Raya o por lo menos te empata. Y aquí tienes
el caso de un teorema, el de los cuatro colores, que no se sabría
aún que era teorema de no haber sido por la ayuda indispensable
del computador.
 |
|
|
Seguro que pronto veremos muchos otros teoremas con el mismo sabor. Pronto veremos también cómo el computador es capaz de enseñarte integrales, de corregir tus ejercicios, de ponerte notas (¡qué horror!). Es de esperar que aprendamos a usarlos bien, porque mal usados nos harán la vida imposible.