El juego que te explicaré ahora es muy viejo y muy interesante. Nim, en inglés antiguo, es «quitar» o «retirar». Entre nosotros se puso de moda a raíz de una célebre película, «El año pasado en Marienbad», en la que el protagonista parece haberse encandilado con el jueguecillo y lo usa para matar el tiempo en el balneario de Marienbad, en Checoslovaquia, famoso en toda Europa desde el siglo 16.

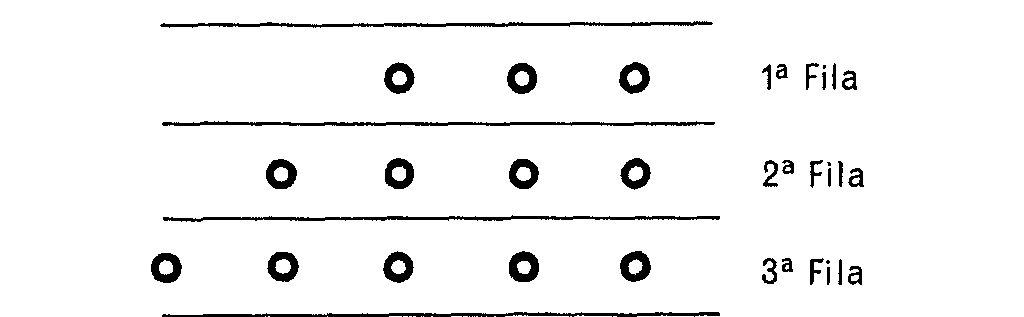
Es unjuego para dos personas, A y B. Se colocan cuatro filas de piedrecillas, el individuo de Marienbad usaba cerillas, una fila con 1, otra con 3, otra con 5, otra con 7 piedrecillas. Nosotros empezaremos jugando con tres filas de piedrecillas en la forma siguiente. Luego veremos que nuestra estrategia es la misma para jugar con cualquier número de filas y piedrecillas en cada fila.
 

El jugador A puede quitar una o más piedrecillas de la fila que escoja. Por ejemplo, retira 2 de la 2ª fila, quedando así las piedrecillas:

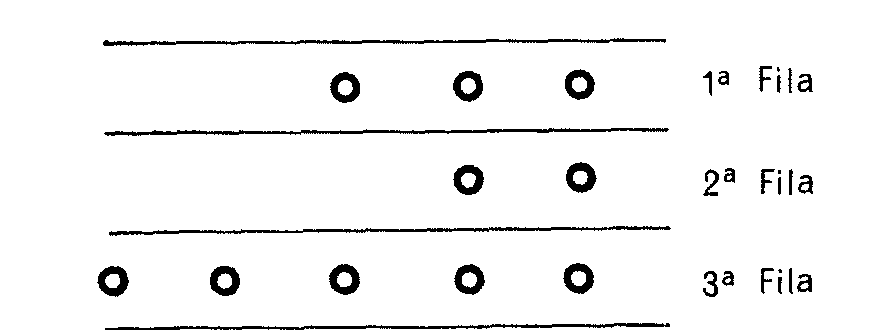
Le toca a B, quien puede retirar las piedrecillas que quiera (siempre una o más) de la fila que escoja. Por ejemplo, quita 2 de la fila 1ª quedando así:
 

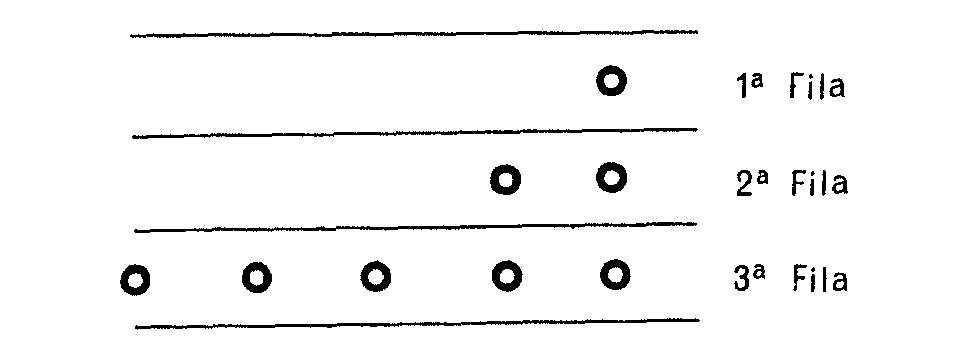Le toca a A, etc... Gana el que se lleve la última piedrecilla.

Si tienes algún amigo o enemigo por ahí cerca, invítale a jugar un rato. El juego es sencillo de aprender y no es nada fácil adivinar una estrategia adecuada para ganar siempre.
 
 

Cuando hayas jugado un buen rato y meditado un poco sobre cómo se debe jugar para ganar, vuelve conmigo, a poder ser, solo. No le digas a tu amigo que alguien te va a explicar la estrategia para ganar, entre otras cosas porque lo que yo te enseñaré te permitirá ganar casi siempre contra cualquiera que no conozca la estrategia y te permitirá ganar siempre contra cualquiera, aunque la conozca, con tal de que tú juegues el primero. Hasta luego.
 
 

La estrategia que te explicaré está basada en el sistema binario de numeración. No te asustes. Verás qué fácil es poner un montón de piedrecillas en sistema binarío sin escribir nada, sin saber siquiera cuántas piedrecillas hay en el montón.

Tienes estas piedrecillas:

Colócalas en fila, así

No hace falta que las cuentes. Ahora, empezando por la izquierda, coge la primera y la colocas debajo de la segunda, coge la tercera y la colocas debajo de la cuarta, etc. Así (no hace falta contar):

Ahora, empezando por la izquierda, coge el primer par y lo colocas debajo del segundo par. El tercer par lo colocas debajo del cuarto par. Así:
 

Ahora coge el primer montón de cuatro piedrecillas y lo colocas debajo del segundo de cuatro piedrecillas, el tercero de cuatro piedrecillas bajo el cuarto (aquí, como no hay siguiente de cuatro piedrecillas, paramos). La cosa queda así:

Ahora, el primer montón de ocho piedrecillas, lo colocas bajo el segundo de ocho (aquí como no hay segundo de ocho no hacemos nada, hemos terminado).

Creo que ya entiendes lo que hemos conseguido. Hemos distribuido las piedras en grupos de 1, 2, 4, 8, 16..., piedrecillas. En nuestro caso resulta 1 de 8 1 de 4, 0 de 2, 1 de 1, es decir, el número de nuestras piedrecillas en sistema bínario es 1101. Observa que no hemos tenido que escribir nada, ni que hacer una sola división, ni siquiera que contar las piedrecillas.

Haz este ejemplo conmigo para practicar.

El número de piedras en sistema binario es 1011. Esto es sólo una preparación. Vamos a nuestro juego. Supon que tú eres el primero en jugar, tú eres A. Tu contrincante es B. Coloca las piedras de cada fila en sistema binario ordenadamente, es decir, de modo que los montones de 8 de las piedras de cada fila queden en una misma columna, los de 4 en otra, los de 2 en otra, los de 1 en otra. Así:

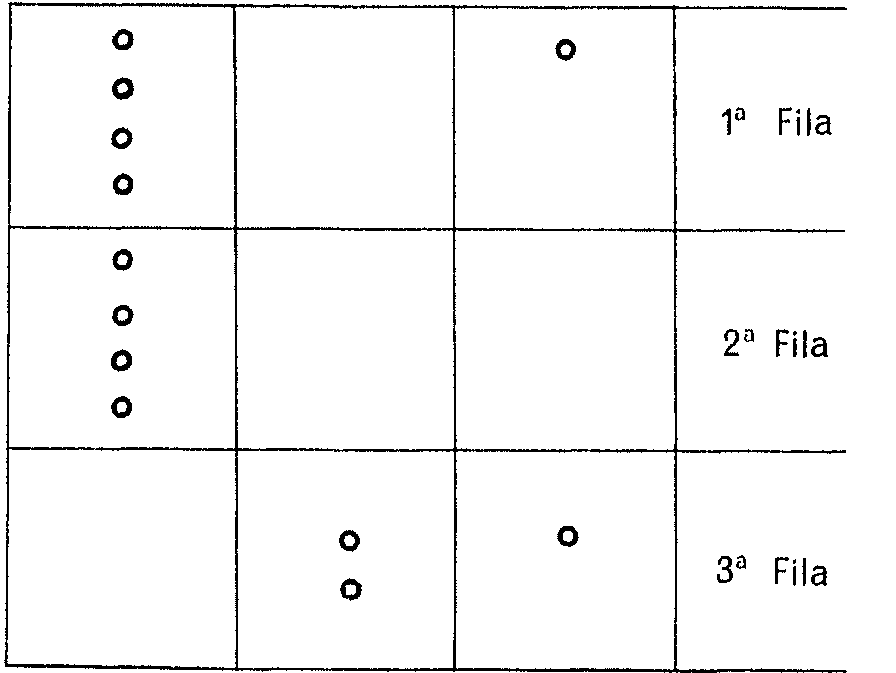
Observa ahora esta disposición de las piedras por columnas. Hay en la primera columna de la izquierda dos grupos de 4 piedrecillas, en la segunda un grupo de dos, en la tercera dos grupos de una piedrecilla. Tu objetivo al jugar va a ser dejar en cada columna un número par de grupos. Así, en este caso puedes quitar los dos de la tercera fila, dejando el juego a B en esta situación:

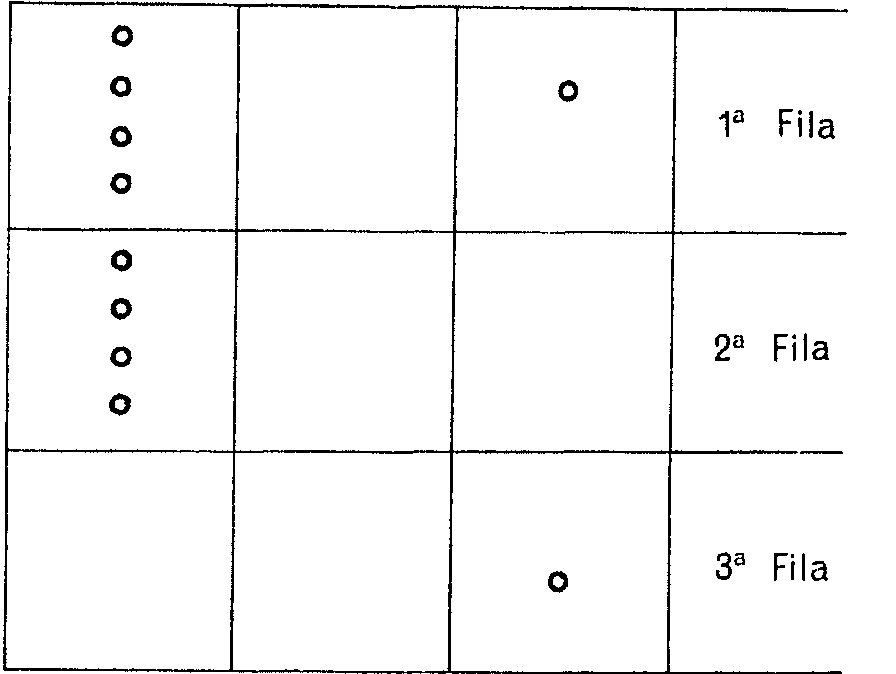
Ahora juega B, que quitará las piedras que le parezca, de la fila que se le antoje. Supon por ejemplo que quita 2 de la primera fila, dejándote a ti esta situación:

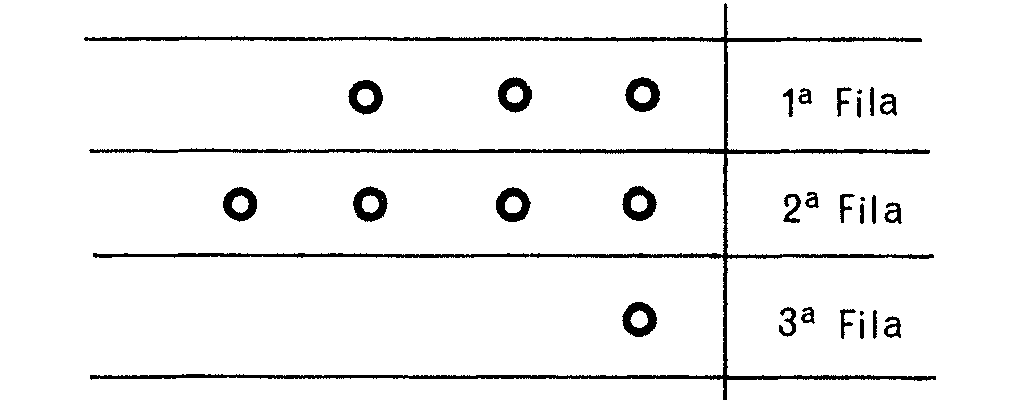
Tú ahora a tu estrategia. Coloca las piedras de cada fila en sistema binario. Así:

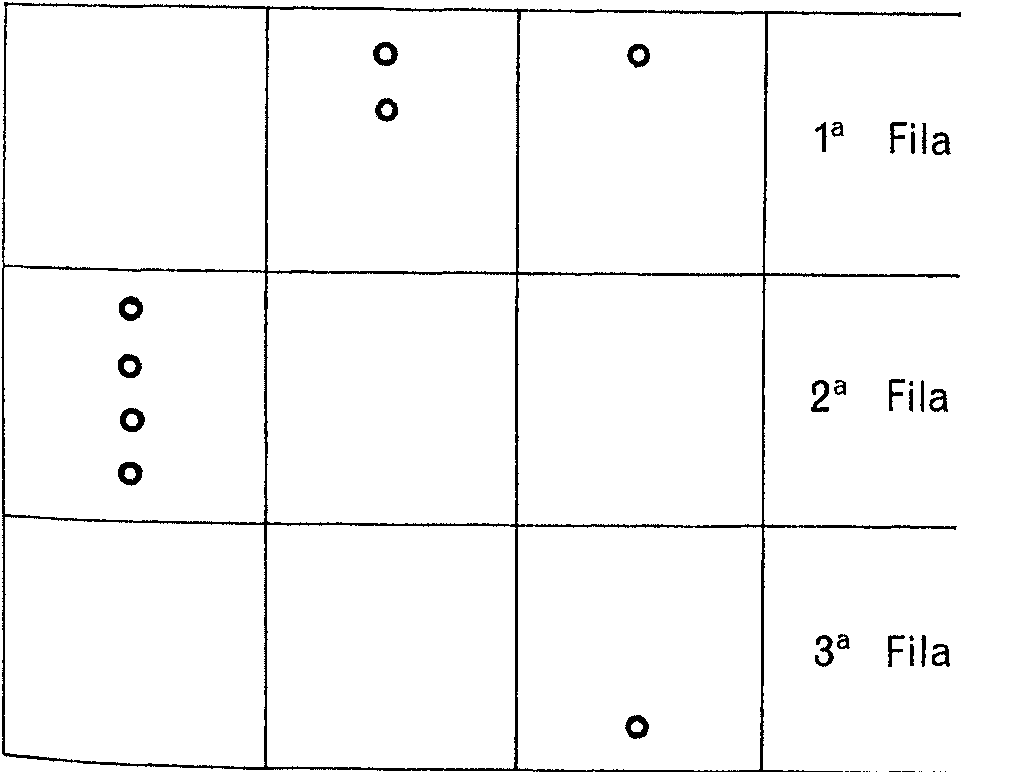
Para seguir con tu estrategia de dejar todas las columnas con un número par de grupos, observa que puedes quitar dos piedras de la 2ª fila y entonces le dejas a B la siguiente situación, al colocar las piedras de cada fila en sistema binario:

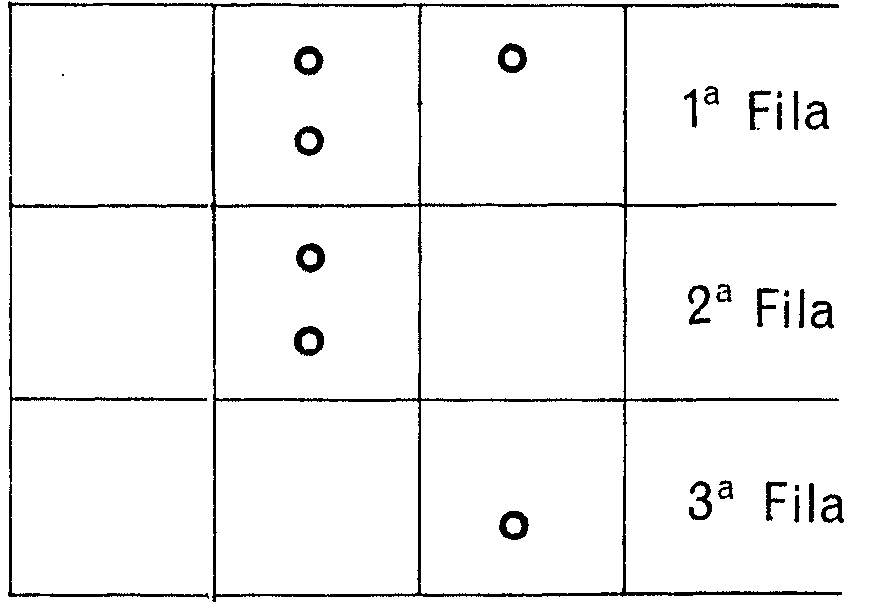
Supon que B coge una piedra de la 2ª fila, con lo que te queda:

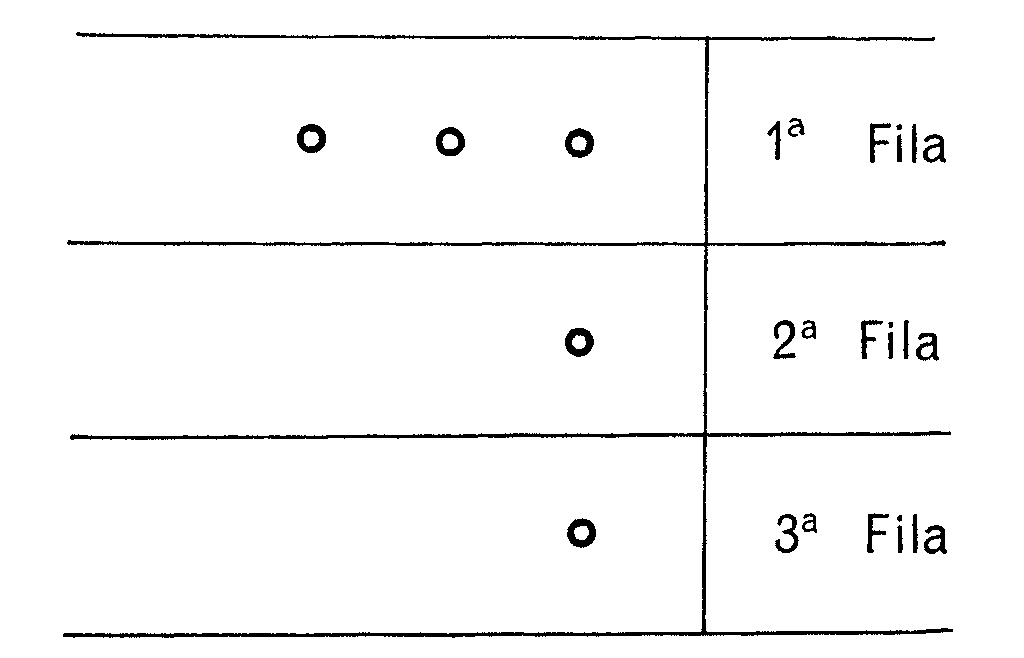
Tú entonces las colocas como siempre en sistema binario.

Observa que si quitas las tres de la fila 1ª le queda a B:

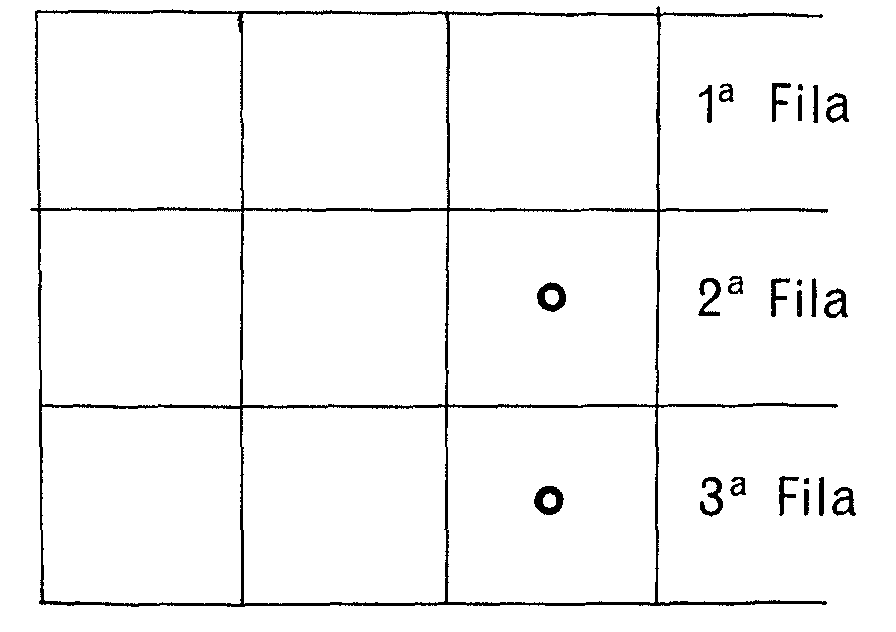
una situación en la que no tiene más remedio que hacerte ganar.

Fíjate bien. El hecho de que el juego se haya empezado con 3, 4, 5 piedrecillas no importa nada en absoluto. Tampoco importa que sólo haya tres filas. Lo que importa únicamente es que puedas llevar adelante tu estrategia: colocar las piedras decada fila en sistema binario ordenadamente y quitar de la fila que haga falta las piedras que hagan falta para que, colocando las piedras en sistema binario, en todas las columnas haya un número par de montones.

Supongamos que empezáis a jugar con cuatro filas de 14, 11, 9 y 7 piedrecillas, respectivamente, y que tú eres A, es decir, juegas primero. La situación inicial en sistema binario es:

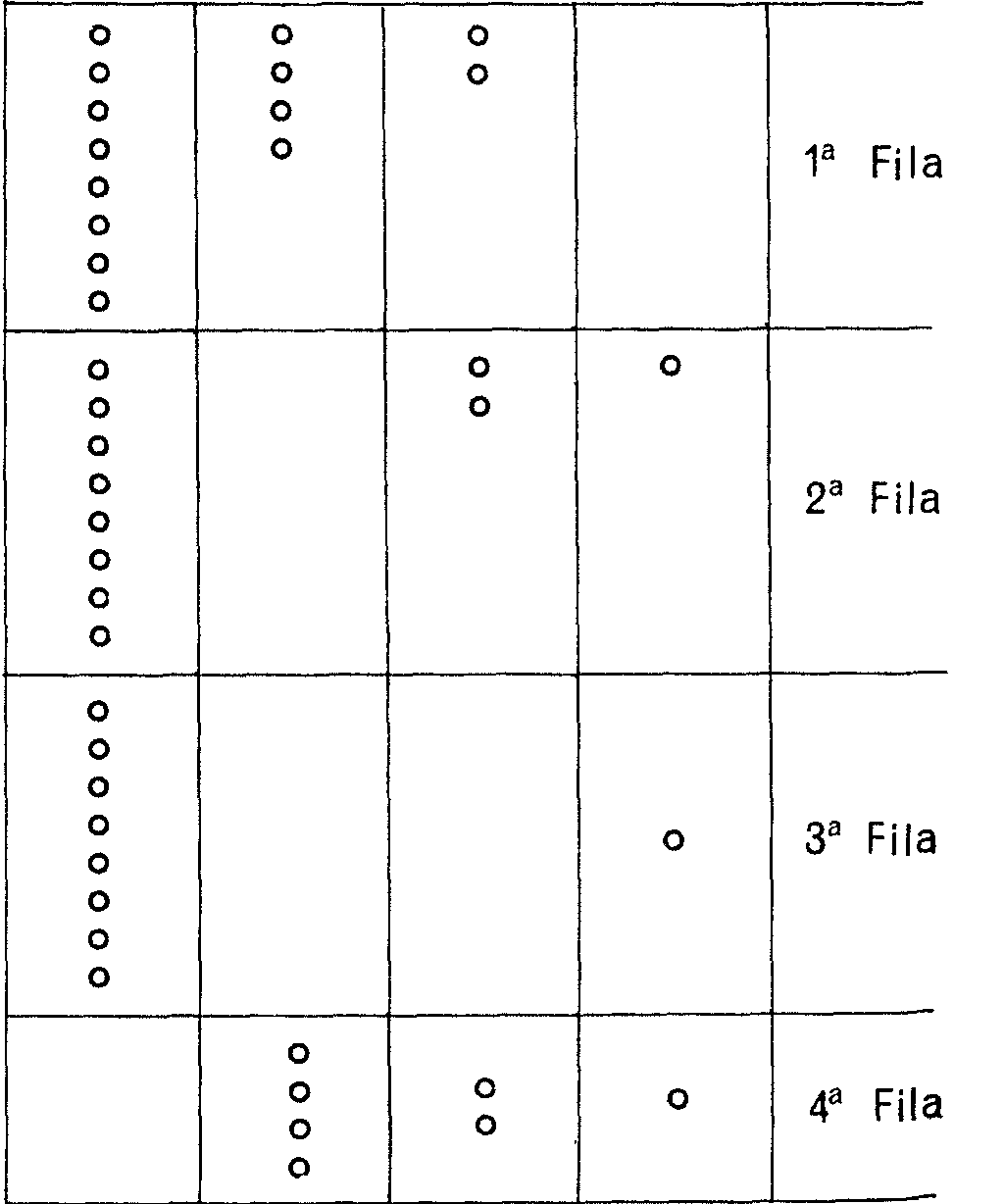
La columna de los montones de 8 tiene 3, la de montones de 4 tiene 2, la de montones de 2 tiene 3 y la de montones de 1 tiene 3. Para llevar adelante tu estrategia, te fijas en la primera columna que tenga un número impar de grupos, que en este caso es la primera de la izquierda, que tiene tres. En cualquiera de estos tres grupos hay ocho piedras. Observa que 8 = (4 + 2 + 1) + 1. Así, desplazando o quitando piedras de las ocho de un grupo cualquiera de estos tres puedes rellenar los otros cuadros de la misma fila o bien dejarlos vacíos si hace falta para que después de tu jugada con las piedras de una sola fila todas las columnas tengan un número par de grupos de piedras. Aquí, por ejemplo, coges las ocho piedras del grupo de ocho de la primera fila, de ellas pones una en el cuadro de las de una piedra y retiras las otras siete, y retiras asimismo las dos del cuadro de dos de la primera fila. La primera fila queda entonces así en sistema binario.

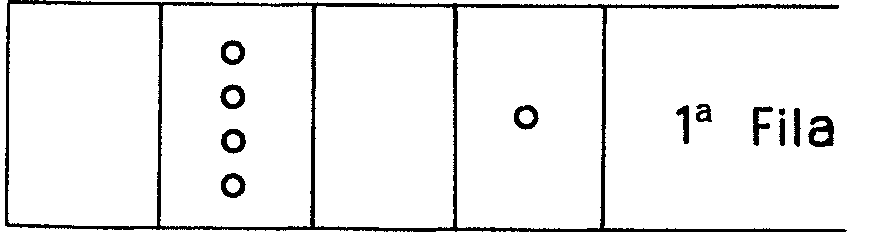
De este modo, cada columna tiene un número par de montones.

Observa los dos hechos importantes siguientes:

1) Siempre puedes llevar adelante tu estrategia con tal que haya alguna columna con un número impar de montones. Si no es así, es decir, si todas las columnas tienen un número par de montones, no te esfuerces en esta jugada. Jugando según las reglas, es decir, cogiendo una o más piedras de una sola fila siempre le vas a dejar a B alguna columna con un número impar de montones y él, si conoce tu estrategia, va a ganarte si la va realizando. Pero si no la sabe, casi seguro que en una jugada posterior te va a dejar las cosas bien para ti.

2) Muchas veces, cuando te toca jugar, tienes varias posibilidades para llevar adelante tu estrategia, pero siempre que haya alguna columna con un número impar de montones, quitando algunas piedras del modo que te he indicado puedes llevar adelante tu estrategia. Por ejemplo, en el último juego complicado que hemos empezado, de la fila 2ª podrías quitar todas las piedrecillas y conseguirías tu objetivo. La otra jugada allí explicada juega con la fila más larga.

Si estás cansado de tanto rollo, descansa y vuelve otro día. Si sólo te interesa ganar todas las veces que se pueda, no vuelvas a este lugar, porque lo que viene a continuación es la explicación matemática de por qué funciona la estrategia que te he dado.

Que la estrategia conduce siempre a la victoria es bastante claro. Si A puede dejar siempre a B una situación en la que en sistema binario hay un número par de montones en cada columna es porque este número par es cero para cada columna (en cuyo caso es que A se llevó todas las piedrecillas en su última jugada y ya ganó) o bien es que hay al menos dos filas con piedras y así B no puede ganar en esta posición (tiene que coger piedras de una sola fila).

Lo que necesita una explicación más detallada es el que A pueda llevar adelante siempre su estrategía, si es que alguna vez estuvo en condiciones de iniciarla, es decir, sí en algún instante, bien al comienzo o bien en algún otro momento del juego, recibió las piedras de tal modo que, colocadas en sistema binario, en alguna columna hubo un número impar de montones. La razón de este hecho es fácil considerando la receta misma que te he explicado antes. El jugador A debe fijarse en la primera columna de la izquierda con un número impar de grupos. En cada uno hay 2^p piedras, por ejemplo 32 = 2⁵ piedras. Observa que

por ejemplo, 32=(16+8+4+2+1)+1.

Así, en uno cualquiera de estos grupos hay piedras suficientes para hacer que los cuadros siguientes de la misma fila queden llenos o vacíos, de modo que todas las columnas queden con un número par de grupos de piedras.

Tú puedes pensar ahora lo siguiente. Supongamos que jugamos con doce piedrecillas y tres filas, empezando por colocar al azar las piedras en las tres filas. ¿Qué probabilidad tengo yo de que, desde el principio, jugando el primero, la situación me sea favorable y me permita aplicar la estrategia de modo que aunque mi contrincante sepa la estrategia, le gane? Trata de calcularla. Casi todas las veces podrás ganar tú. Exactamente una sola vez de las doce posibles distribuciones te sale la situación mala, que es 2, 4, 6. Todas las demás te son favorables.

El Nim, con esta estrategia, está programado para que lo puedan jugar.... y ganar, los computadores. Pero no te asustes si tienes que jugar contra uno de ellos. Dile que aceptas, pero que tú quieres jugar con 25 filas. El computador tal vez se arrugará si es que no está programados para más de 10 filas. Está bien que el computador aprenda que todavía hay clases...
 
 

NOTAS

Hay muchos juegos con el sabor del que acabas de ver y que tal vez te hayas encontrado por ahí, jugando con maquinitas. Uno muy antiguo, para dos jugadores, consiste en poner un montón de piedrecillas. El primer jugador, A, puede quitar 1, 2 ó 3 piedrecillas. Deja el tumo a B, quien puede quitar asimismo 1, 2 ó 3 piedrecillas. Gana quien se lleve la última piedra. Este juego tiene una estrategia muy sencilla. Si los dos jugadores la conocen y la practican ya se sabe desde el principio quién va a ganar, dependiendo del número inicial de piedras. Piensa un poco y descúbrela.

El Nim, lo mismo que este juego, admite variantes sencillas, como por ejemplo que pierda el que se lleve la última piedrecilla. ¿Cómo varía entonces la estrategia? También se puede pensar en combinar los dos juegos. Se colocan varios montones de piedras, por ejemplo tres, uno con 3, otro con 4 y otro con 5 piedras. Se pueden quitar 1 ó 2 piedras de un solo montón. ¿Te atreves a tratar de encontrar una estrategia?