Los puentes de Königsgsberg

Una de las ramas importantes de la matemática actual, la topología, nació con el siguiente acertijo que el gran Euler describió y resolvió en uno de sus artículos: "El problema que, según entiendo, es muy bien conocido, se enuncia así: En la ciudad de Königsberg, en Prusia, hay una isla, llamada Kneiphof, rodeada por los dos brazos del río Pregel. Hay siete puentes, A, B, C, D, E, F y G, que cruzan los dos brazos del río (ver la figura de abajo). La cuestión consiste en determinar si una persona puede realizar un paseo de tal modo que cruce cada uno de los puentes una sola vez. Se me ha informado de que mientras unos negaban la posibilidad de hacerlo y otros lo dudaban, nadie sostenía que fuese posible realmente".

¿Por dónde se puede empezar a atacar el problema? Piensa y observa. Hay muchos aspectos del problema que son totalmente irrelevantes, que no importan nada. Por ejemplo, que la isla sea más grande o más chica, que los puentes sean más estrechos o más anchos, rectos o curvos, más largos o más cortos. Lo esencial es el esquema, lo que los puentes unen y cómo estas uniones se comportan entre si. 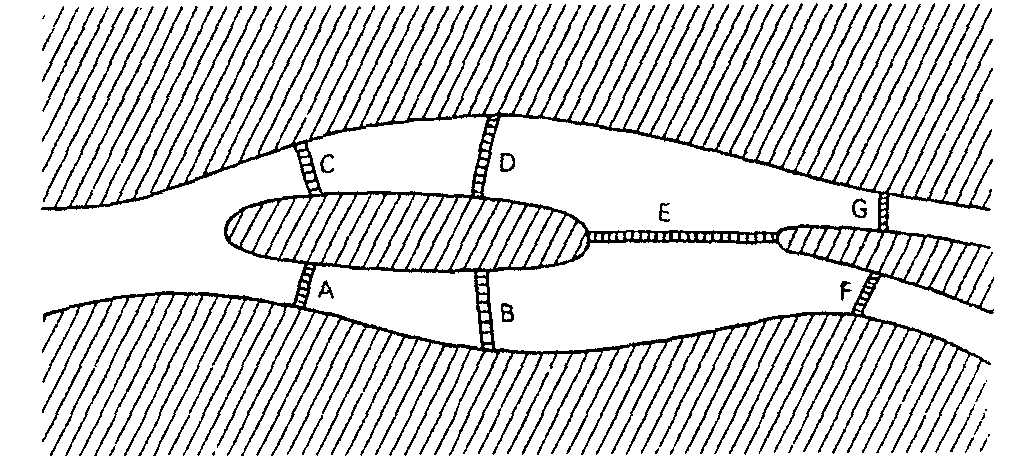Lo esencial es, pues, lo siguiente: ¿Se puede trazar el siguiente dibujo de un solo trazo sin repetir ninguna línea?

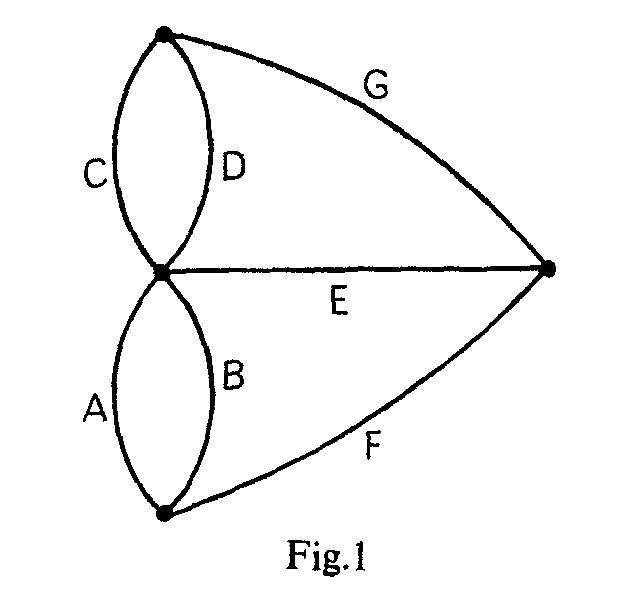Graphics (p.1-6)

Seguro que esto ya te sugiere algún recuerdo de tu infancia. ¿Sabrías repetir las siguientes figuras sin levantar el lápiz del papel y sin repetir dos veces una misma línea? ¿Sabrías hacer esto mismo saliendo de algún punto y volviendo al mismo punto?

Graphics (p.2-1)

Prueba, prueba... La figura 3 la conocerás casi seguro y la habrás hecho muchas veces, pero te costará terminar en el punto en que comienzas. La figura 4 es tan fácil de trazar que, a no ser que lo hagas a mala idea, saliendo de cualquier punto llegas al mismo punto sin repetir arcos y recorriéndolos todos, y eso casi sin proponértelo, La figura 2 parece más simple, tiene menos trazos, pero para ella, como para esta figura 6 de sólo tres trazos,

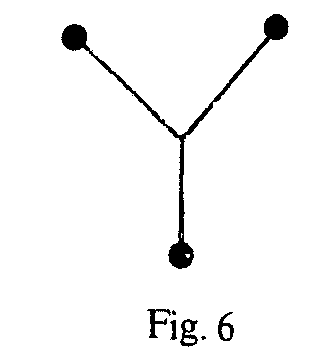
los dos problemas propuestos son imposibles de modo clarísimo, trivial, como a veces se dice insultantemente. La figura 5 parece que no hay cristiano (ni moro) que la analice, pero ahí tienes una solución:

Graphics (p.2-5)

¿Cuál es el misterio de los arcos de un caso y de otro? ¿Cómo averiguar si un dibujo se puede hacer como se pide y otro no? Y si se puede, ¿cómo encontrar la receta?
Empecemos por casos sencillos:

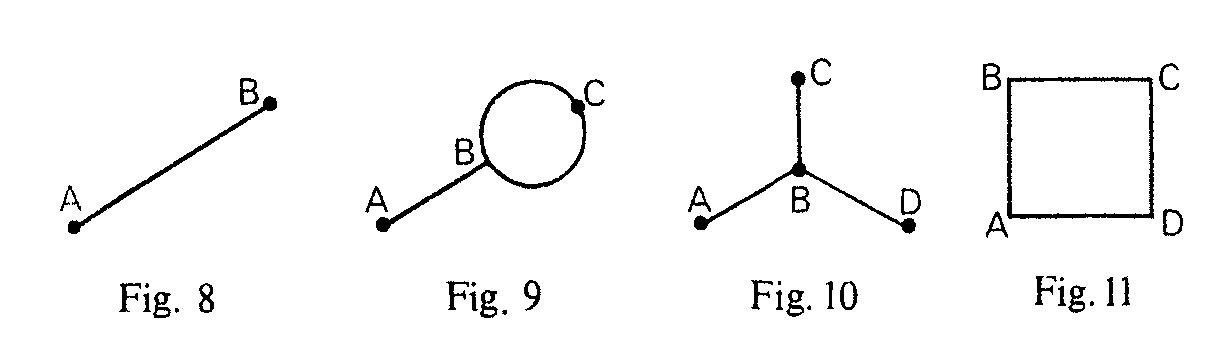
Graphics (p.3-1)

La figura 8 se puede, ¡faltaría más!, pero no se puede salir y llegar al mismo punto. La figura 9 se puede si se sale de A terminando en B y también se puede conseguir si se sale de B terminando en A, pero si salimos de C no se puede. La figura 10 no se puede de ninguna forma. La figura 11 se puede saliendo de cualquier punto y se termina en el mismo punto. Lo que distingue a los vértices es claro. El número de posibles entradas y salidas de ellos, es decir el número de arcos que concurren en cada uno. Aquí están esos números, el grado de cada vértice:

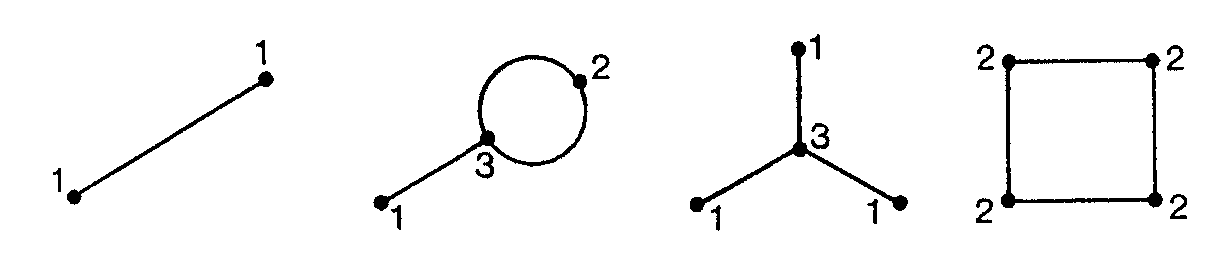
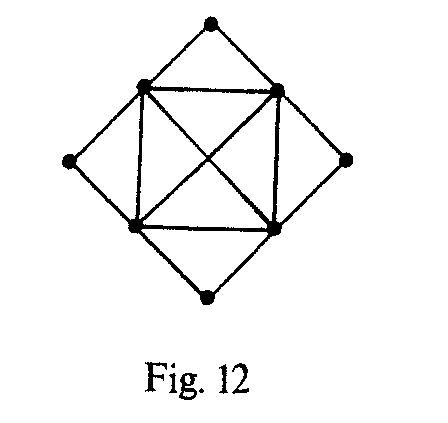
¿Y por qué es importante ese número? ¡Hombre! Entradas y salidas es lo que andamos buscando. Lo que nos atasca en un vértice es la falta de una salida, ¿no? Es cierto, pero tener muchas entradas y salidas no siempre es bueno. La figura 12 tiene más entradas y salidas que la figura 3 y sin embargo la 3 es posible y la 12 imposible. Pensemos en una figura posible de trazar volviendo al mismo vértice de partida. Para cada vértice del recorrido, como no nos paramos en él, resulta que entramos tantas veces como salimos, naturalmente por arcos

distintos. Así, cada vértice es de grado par. El primero también pues volvemos a terminar en él.

Así, si una figura es posible terminando en el mismo vértice de salida tiene que tener todos los vértices de grado par.

¿Aclara esto nuestro problema totalmente? ¡Aún no! ¿Resultará que si todos los vértices son de grado par podemos hacer un recorrido llegando a terminar en el vértice de salida? Veamos. Lo que es seguro es que nunca nos atascamos en nuestro camino si no es en el vértice de salida S, pues como cada vértice es de grado par, al entrar en uno que es distinto de S por primera vez nos queda un número impar de arcos de salida, es decir, por lo menos un arco, al entrar por segunda vez nos queda de nuevo un número impar, pues hemos usado tres arcos que concurren en ese vértice; así, siempre que entremos podremos salir. Por tanto, caminando por nuestra figura al buen tuntún saliendo de S sólo nos atascamos estando en S de nuevo. Si hemos recorrido toda la figura ya tenemos nuestro problema resuelto. ¿Y si no la hemos recorrido? Si en nuestro camino C nos faltan arcos por recorrer, lo cierto es que podemos proceder así para ampliar nuestro camino y hacer uno más grande que siga verificando las reglas del juego. Cuando lleguemos al primer vértice S₁ del que salen arcos que no estén recorridos, vamos por ellos. Como antes, no nos podemos parar si no es en S₁. Ahora, cuando en S₁ están recorridos todos los arcos que salen de él, seguimos a partir de S₁ por el camino inicial C hasta llegar al primer vértice S₂ en el que concurran arcos que no están recorridos ni en el camino C ni en la ampliación que acabamos de hacer. Así, acabamos por recorrer todos los arcos.

Por tanto, si todos los arcos son de grado par, la figura propuesta es posible y además tenemos la receta para trazar el camino pedido. ¡Además esta receta nos dice que el vértice de salida, que puede ser cualquiera, es necesariamente el mismo que el final!

¿Y si hay vértices impares? Observa de nuevo la figura 9.

Si sales de A o de B, consigues hacerla, pero si sales de C, no. Los vértices A y B son impares, el C es par. ¿Qué misterio es éste? Lo que antes nos condujo a la solución nos puede indicar la forma de proceder ahora. En un trazado como el que tenemos que hacer hay un vértice inicial, un vértice final y todos los demás de paso. Pero un vértice de paso (ni inicial ni final) tiene tantos arcos de entrada como de salida, es decir, es de grado par. Por tanto si una figura admite un trazado como el que se pide, todo vértice de paso ha de ser par. Pero los vértices de paso son todos menos dos. Por tanto, si una figura tiene más de dos vértices impares, es imposible. Por otra parte, si una figura tiene dos vértices impares, está claro que si intentamos trazarla según las reglas, tendremos que salir de uno de los vértices impares e intentar terminar en el otro vértice impar. Sólo nos queda una cuestión para tener nuestro problema resuelto totalmente. Si una figura tiene dos o sólo un vértice impar, ¿será posible?, ¿receta? Lo que hasta ahora sabemos nos puede aclarar las cosas. Si una figura tiene uno o dos vértices impares, salimos con decisión de uno de ellos S. No nos podemos atascar en ningún vértice par, pues si entramos podemos salir de él, ni tampoco en S, pues al salir gastamos uno de sus arcos y así le quedan después un número par de ellos y, por tanto, si volvemos a entrar podemos salir. Como acabamos por atascarnos (sólo hay un número finito de arcos) queda claro que nos atascamos en el otro vértice impar, lo cual demuestra que no puede haber un solo vértice impar. Ahora nos preguntamos: ¿hemos recorrido con este camino C toda la figura? Si es así, enhorabuena, ya tenemos nuestro problema resuelto. ¿No? Entonces procedemos como antes. Salimos de S por el camino C hasta llegar al primer vértice S₁ del que salen arcos no recorridos del camino C. Observa que a todos los vértices que tienen aún arcos no recorridos en C les falta un número par de arcos por recorrer. Así, saliendo de S₁ por arcos que no están en C no nos atascamos en ningún vértice distinto de S₁. Así llegamos a S₁ por un camino C₁ de arcos que no están en C habiendo recorrido todos los arcos de S₁ que no estaban en C. Ahora podemos continuar por C hasta llegar al primer vértice S₂ que tiene arcos que no están en C ni en C₁. Procedemos igual, y de este modo acabamos por recorrer todos los arcos de la figura.

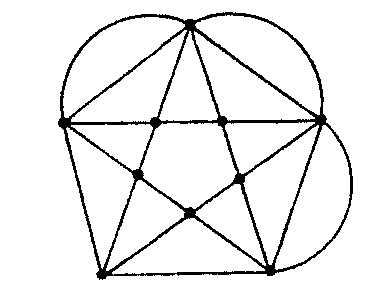
Puedes practicar el método proponiéndote figuras posibles complicadas y desafiando a algún amigo a trazarlas. Por ejemplo, las siguientes.

Graphics (p.4-3)

Graphics (p.4-4)

También puedes suponer que tienes una avioneta en Königsberg, que te permite dar un único salto de un punto a otro cualquiera, el que te apetezca. ¿Podrías entonces hacer el camino que se pide? ¿Cuál es la condición general de una figura para que se pueda trazar con la ayuda de un salto único?

NOTAS

El método que hemos visto para resolver problemas como el de los puentes de Königsberg nos permite también resolver el problema de llegar al centro de cualquier laberinto que se nos ponga por delante, aun sin conocer en absoluto su estructura. Propongámonos llegar desde la entrada al punto del tesoro señalado en el laberinto del jardín de R. Ball, uno de los más grandes escritores de recreaciones matemáticas de todos los tiempos. Supongamos que no tenemos ningún mapa y que por lo tanto nuestra finalidad deberá ser recorrer todo el laberinto (se supone, claro, que el tesoro está bien patente en algún punto del laberinto al que se puede llegar) y salir por la única entrada que hay. ¿Podremos hacerlo?

¡Sí! El sendero que constituye el laberinto (línea en cursiva de la segunda figura) consta de arcos y puntos de bifurcación. Como por cada arco queremos pasar una vez de ¡da y otra de vuelta, repetimos cada arco dos veces. Una vez hecho esto, claramente tenemos una figura como las que hemos venido estudiando en este capítulo con todos los vértices pares. Así se puede recorrer toda ella sin repetir arcos partiendo de cualquier punto. Además, lo podemos hacer sin conocer el mapa del laberinto. Lo único que necesitamos es poder señalar de algún modo los arcos que ya hemos recorrido.

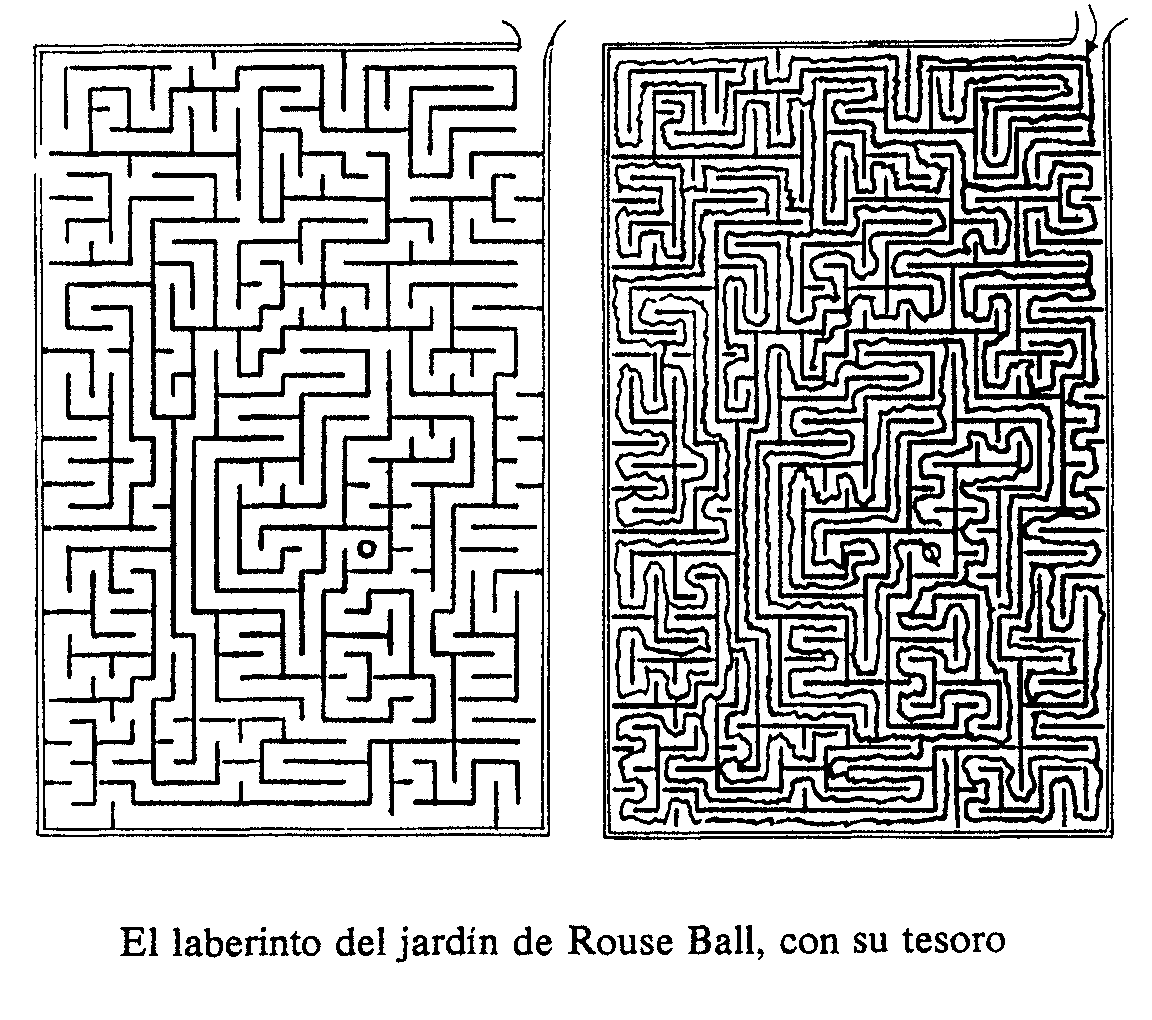
Graphics (p.5-4)

Para ello basta que con una tiza, en cada bifurcación señalemos con una flecha qué sendero hemos tomado para no volverlo a tomar cuando estemos en el mismo punto.

Naturalmente, este modo de proceder no nos proporciona el camino más breve para llegar al tesoro, pero sí nos da la seguridad de llegar a él y de poder volver a salir.