El secreto del Salón Ovalado

Les siguieron, naturalmente con gran sigilo, los contraespías, y a éstos, los contracontraespías. El Rey, con paso tranquilo, pero decidido, se dírigió hacia un lado del ovalado salón. El Ministro, por su parte, con el mismo paso decidido, pero tranquilo, se dirigió en dirección contraria al otro lado del salón ovalado. Los espías los observaban de reojo mientras consultaban en sus libretas «parece», «focos», «rebeldes» y «exigen». Los contraespías estaban atentos a los espías, y los contracontraespías no perdían de vista ni un momento a sus contraespías correspondientes. El Rey se paró un momento y el Ministro, respetuoso, se paró también en su camino. Estaban a más de 20 metros de distancia cuando un espía más astuto observó y apuntó en su libreta: «Este Ministro, o habla solo o está rezando». Pero nadie pudo oír nada. Sólo el Rey pudo percibir claramente en sus oídos el mensaje del Ministro: «Majestad, con todos mis respetos, su bragueta está totalmente abierta».
 
 

El misterio del Salón Ovalado consiste fundamentalmente en que en una elipse como ésta
 

existen dos puntos, los focos F₁ y F₂, tales que si las paredes de la elipse fueran de goma como las de un billar y se lanzase una bola desde F₁ en cualquier dirección, al rebotar iría a pasar por F₂. El sonido se comporta al rebotar como la bola. Por ello hablando muy bajo, muy bajo en F₁ puede llegar la voz a F₂con suficiente intensidad para que se entienda, pues llega a F₂de todas las direcciones que salen de F₁. En otro punto cualquiera llega sólo el sonido hacia él dirigido y no se percibe suficientemente.

Algunas estaciones de Metro tienen una sección con un techo aproximadamente elíptico. Haz este experimento. Coloca a un amigo en el andén opuesto y busca el punto en tu andén tal que cuchicheando tú un mensaje secreto, él te pueda oír. ¡Ah! Procura no cuchichear mientras está pasando uno de esos monstruos infernales. Entonces no suele salir el experimento.

¿Y quién ha dicho que la elipse tiene tan maravíllosa propiedad? Sí que lo sabes y lo hemos visto antes. Recuerda «Las matemáticas de un bocata». Pero permíteme que sea pesado y lo repita.

Con centro en F₁ traza la circunferencia de radio 2a, longitud del eje mayor de la elipse. Toma un punto M de la elipse y únelo a F₁ y F₂. Como MF₁ + MF₂= 2a, resulta que si prolongamos MF₁ hasta N en la circunferencia, 2a = MF₁+ MN y así MN = MF₂. Si se traza t, la mediatriz de NF₂, resulta que t tiene un punto M común con la elipse. ¿Tendrá más? No, porque SF₁ + SN > N F₁ = 2a (un lado de un triángulo es menor que la suma de los otros dos). Así, t es la tangente a la elipse en M. Ahora, cuando una bola rebota en una curva, rebota como si la curva se sustituyese por su tangente.

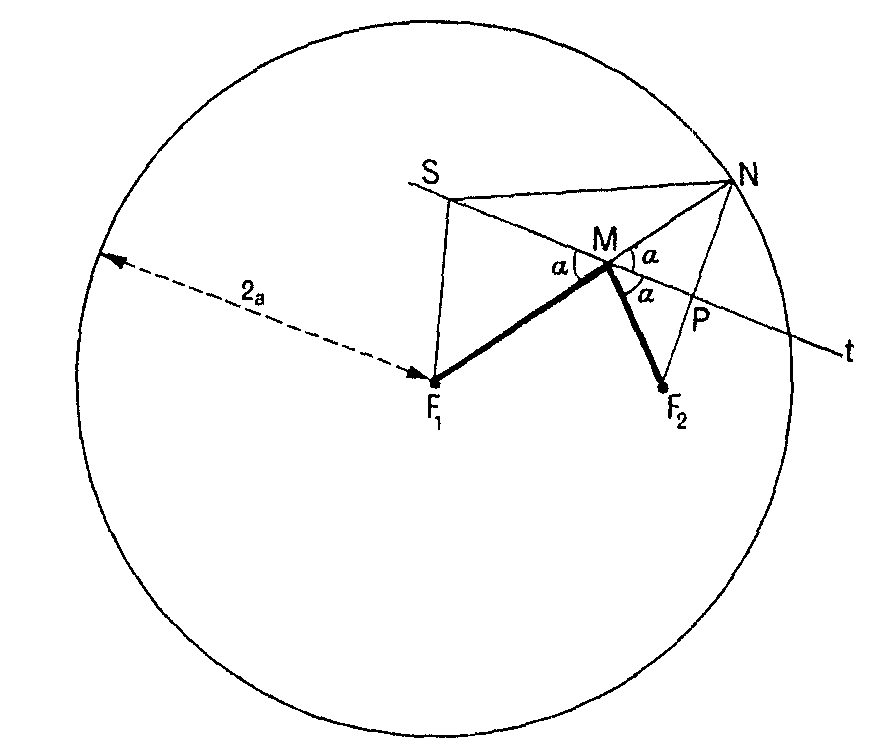
La bola lanzada desde F₁ a M rebotaría en t formando ángulos iguales de entrada y salida con t. Pero como el ángulo F₁MS es igual al ángulo NMP (opuestos por el vértice) y NMP es igual al PMF₂ (simetría respecto de t), resulta claro que la bola desde F₁ hacia M rebota hacia F₂.

¿Sabes que los telescopios más potentes tienen un enorme espejo parabólico? ¿Por qué? Los rayos de luz que nos llegan de una estrella prácticamente paralelos son recogidos por el espejo parabólico colocando su eje en dirección de los rayos y al reflejarse vienen a parar al foco de la parábola. Curioso, ¿no? ¿Para qué? La luz que llega de un estrella es muy tenue. Si se reúne en un punto toda la que llega por la gran abertura de un telescopio parabólico ya es mucho mayor. ¿Cómo es esto? Parecido al truco de la elipse. La parábola es el conjunto de puntos del plano que equidistan de un punto, el foco, y de una recta, la directriz. Se trata de ver cómo se refleja el rayo r paralelo al eje, al incidir en un punto M de la parábola.

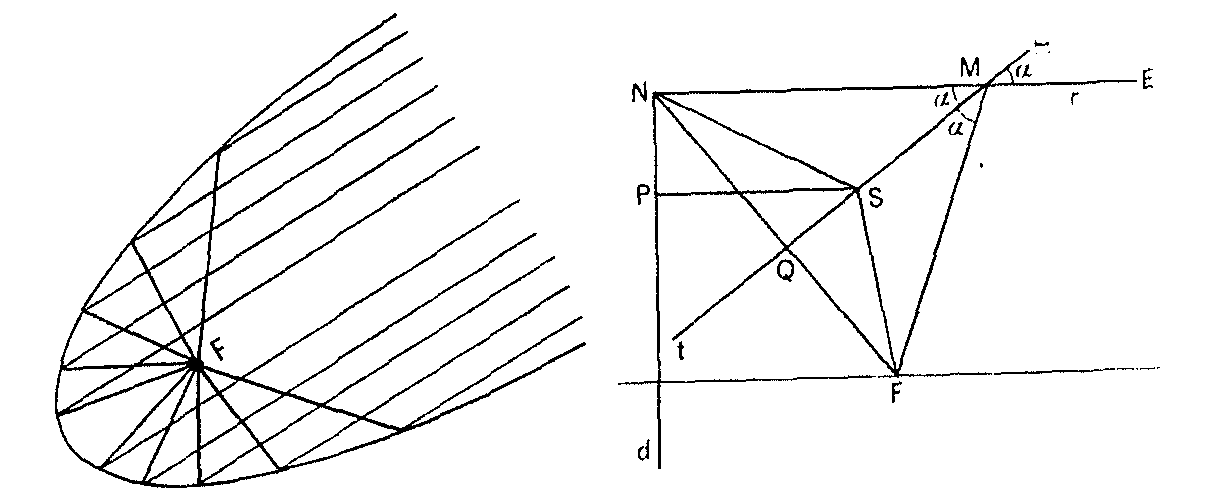
Para ello hay que ver cómo es la tangente en M a la parábola. Puesto que MN = MF, la mediatriz de NF pasa por M. ¿Tiene algún otro punto en común con la parábola? No, porque SF = SN > SP (hipotenusa mayor que cateto). Así, t es la tangente en M. Ahora, ángulo EMH = ángulo NMQ = ángulo QMF, y así el rayo r viene a reflejarse hacia F.

A Lewis Carroll, el autor de Alicia en el País de las Maravillas, le gustaban mucho los rompecabezas y juegos matemáticos, como se puede adivinar a través del estilo de Alicia. Se cuenta que cuando salió publicado el libro de Alicia, a la reina Victoria de Inglaterra le gustó tanto que pidió que le fueran enviando lo que publicase su autor. La siguiente obra que recibió fue... ¡un tratado de geometría! Lewis Carroll, seudónimo de Charles L. Dodgson, era profesor de Matemáticas. Lewis Carroll, entre otras muchas ingeniosidades, se fabricó un billar elíptico. Como puedes imaginar fácilmente, tiene que ser interesante jugar en un billar elíptico. Suceden cosas curiosas. Una bola que sale de un foco F₁ sin efecto pasa por el otro foco F₂ , luego por F₁, luego por F₁, ... Además la dirección de la bola se va aproximando a la del eje mayor. En cambio, si una bola pasa por un punto del segmento que une los focos sin pasar por ellos, pasará siempre (si no parase) por entre los focos y la envolvente de su trayectoria es una hipérbola con los mismos focos. En cambio, si la bola corta en algún momento al eje mayor entre un foco y el punto más cercano a él de la elipse, por siempre cortará al eje mayor entre los focos y la elipse. ¿Por qué no tratas de demostrarlo? Es bastante sencillo con lo que ya sabes.

Aquí tienes otro problema interesante para pensar. Si lo resuelves, no dejes de dar un gran salto de alegría, porque el problema, aunque parece sencillo, lleva abierto muchos años sin que nadie haya sido capaz de dar con su solución.

Puestos a hacer billares raros, hagamos uno más, esta vez poligonal. La pregunta es: ¿Existe algún billar poligonal tal que haya en él dos puntos M, N, situados de modo que una bola colocada en M, se lance como se lance, no puede llegar nunca al punto N? Naturalmente, se supone que la bola no para nunca.

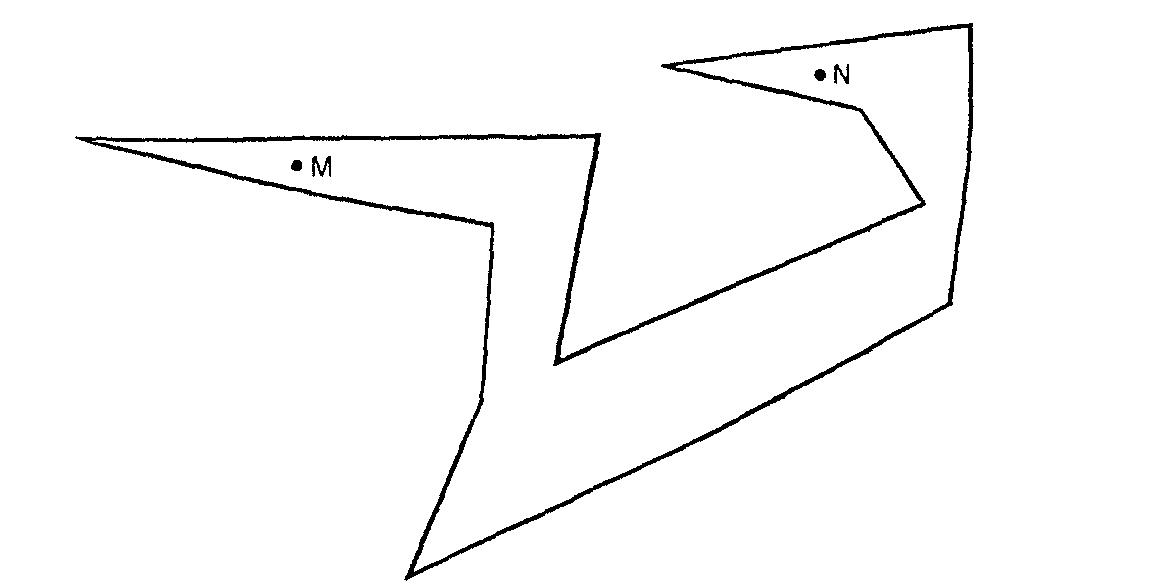
Se puede construir muy fácilmente un billar curvo con esta propiedad, de la siguiente manera, basada en las propiedades que conocemos de la elipse:
 

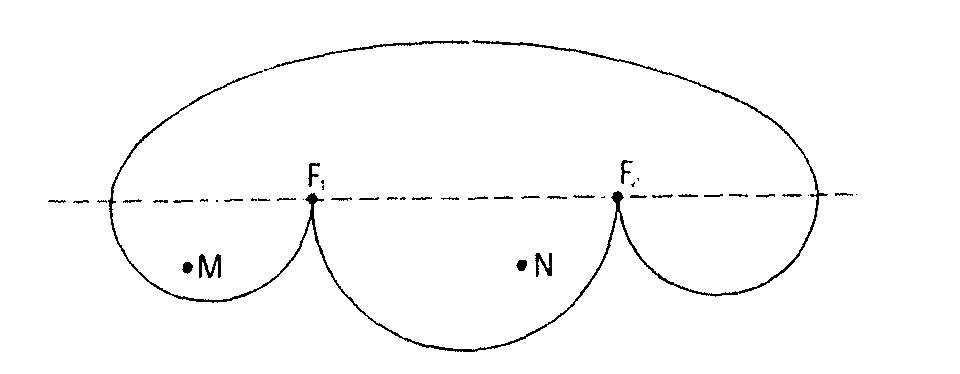El trozo de arriba es media elipse de focos F₁ y F₂ . Los otros trozos del borde son semicirculares. Si M y N están colocados como se indica, por más reflexiones que haga, una bola que sale de M nunca llega a pasar por ningún punto del semicírculo de diámetro F₁F₂ . Si no se permiten más que bordes rectilíneos, el billar poligonal, no se sabe aún si existirá algún billar con una propiedad semejante. ¿Te animas a pensar un poco?

Sin embargo, el nombre de Paseal se ha hecho más famoso aún como filósofo de la religión y como escritor, ocupando así un lugar único en la historia del pensamiento. Antes de cumplir sus treinta años, Pascal había adquirido un renombre incomparable como matemático y físico. A partir de 1654, después de una honda experiencia religiosa, que él llamó su «noche de fuego», decidió dedicarse enteramente a una vida de oración y de pensamiento religioso.

Sus obras más importantes en este aspecto son Las cartas provinciales, de gran influencia en su tiempo, y sobre todo los fragmentos hallados después de su muerte de la gran obra que planeaba en forma de una Apología de la religión cristiana.