LA MEJOR IDEA DE ARQUÍMEDES
El cálculo
del volumen de la esfera fue uno de los descubrimientos que Arquímedes
más estimaba de todos los muchísimos que hizo en su vida.
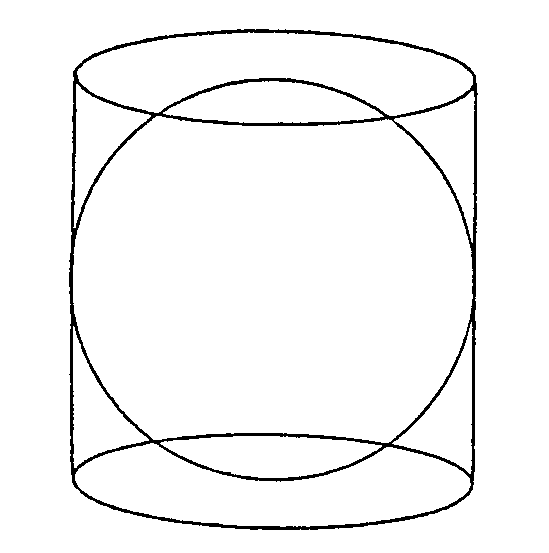
Llegó a demostrar de un modo muy original que el volumen de la esfera
es igual a dos tercios del volumen del cilindro circular circunscrito a
ella. Tanto le impresionó esto a él mismo que mandó
que en su tumba se grabase esta figura en recuerdo de la mejor de sus ideas.
Vamos a ver
cómo llegó hasta ahí. Arquímedes se imaginó
una semiesfera y junto a ella un cilindro circular recto y un cono recto,
ambos de base igual a un círculo máximo de la semiesfera.
Algo así
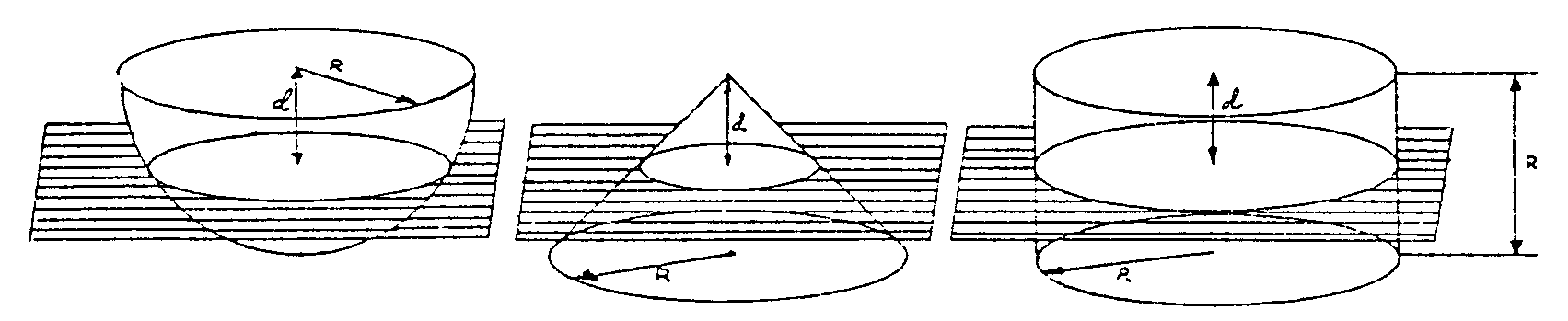
Arquímedes cortó las tres figuras por un
plano paralelo a la base del cilindro y cono y se preguntó cómo
serían las secciones determinadas por este plano en cilindro, semiesfera
y cono.
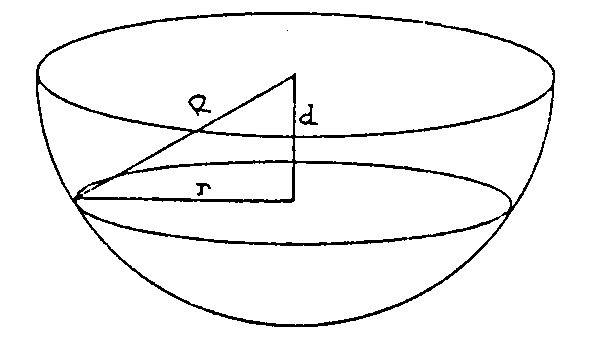
En el cilindro
está claro: un círculo de radio R. En la esfera también
será un círculo, pero su radio dependerá de la distancia
d. Mirando la figura siguiente y acordándote del teorema de Pitágoras,
fácilmente puedes escribir que si el radio de la sección
es r, entonces r2 + d2=R2.
En el cono la sección también será
un círculo y ahora el radio es aún más fácil
de determinar mirando a la figura siguiente
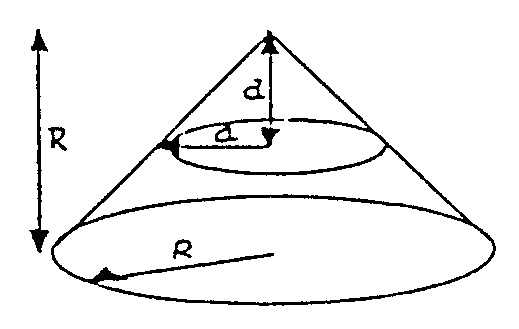
Como el radio de apertura del cono es de 45º, resulta
que el radio es d. Así
Sección cilindro = PR2
= P(r2 +
d2) = Pr2
+ Pd2 =Sección
semiesfera + Sección cono
Las secciones son como rebanadas de las tres figuras obtenidas
cortando paralelamente a la base del cilindro. Resulta que, colocando las
tres figuras como las hemos puesto y cortándolas en rebanadas finas
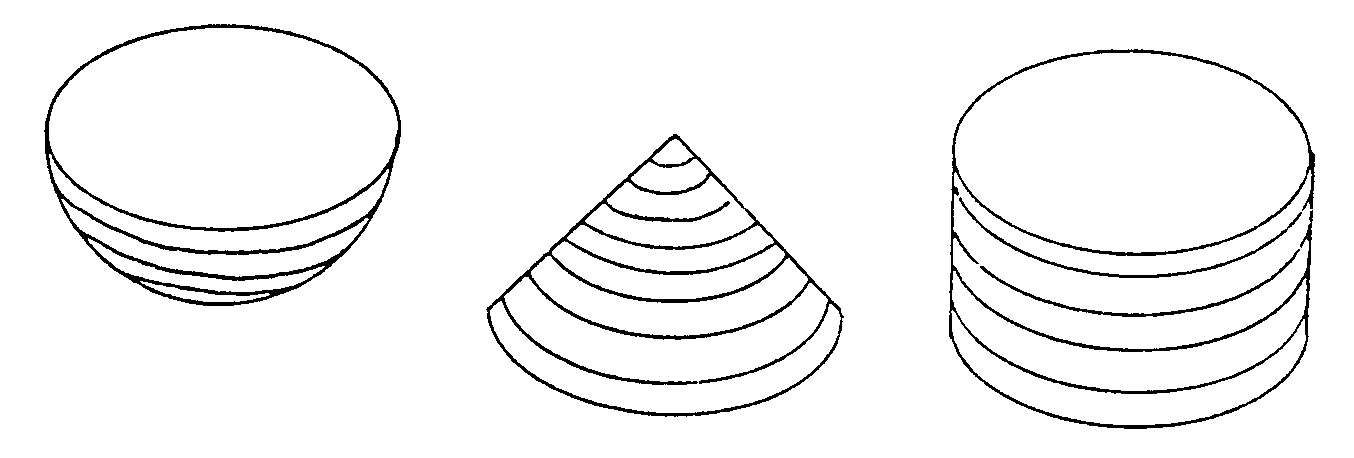
Rebanada en cilindro a altura d = Rebanada en semiesfera
+ Rebanada en cono. Si para cada altura d se tiene esta relación,
parece bastante claro que
Volumen cilindro = Volumen semiesfera + Volumen cono
Pero, como Arquímedes muy bien sabía,
Volumen cilindro= PR3;
Volumen cono= PR3/3
y así resultaba
Volumen semiesfera = 2PR3/3
y Volumen esfera = 4PR3/3.
Cuando Cicerón
fue nombrado cuestor en Sicilia (75a. de C.), descubrió, gracias
a la inscripción que Arquímedes había mandado grabar,
la tumba de Arquímedes que sus paisanos de Siracusa habían
perdido de vista. Cicerón la restauró, pero más tarde
se volvió a perder. Hace unos pocos años se encontraron dos
tumbas que se disputan la autenticidad...
La esfera
puede considerarse como compuesta por un montón de pirámides
de vértice el centro de la esfera y base de área muy pequeña
S sobre la esfera. Esto da una idea de lo que puede valer el área
de la superficie esférica. El volumen de la esfera es 4PR3/3.
El de cada pirámide será RS/3 (pues la altura de cada pirámide
es R). Sumando todas las pirámides y sacando R/3 factor común
resulta
4PR3/3
= Volumen esfera = Suma volúmenes pirámides = Area esfera
x R/3 y así
Area esfera = 4PR2








