Demostración del lema 2. 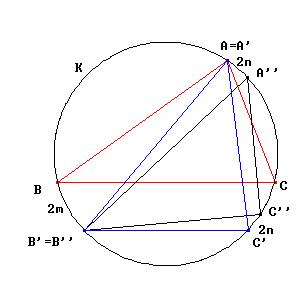    Basta observar en la figura el valor de los ángulos de los triángulos sucesivos ABC (triángulo rojo), A'B'C' (azul), A''B''C''(negro), siendo 2m y 2n los arcos correspondientes a las dos transformaciones sucesivas: A,B,C
A'=A-2m, B'=B+m, C'=C+m
A''=A-2m+n, B"=B+m-2n, C''=C+m+n Es fácil ver que podemos elegir m y n tales que A''=B''=C''=60º, (basta para ello hacer m = (180-B-2C)/3, n = (B - C)/3) y que la magnitud del ángulo que entonces el lado B'' C'' forma con BC vale precisamente (C-B)/3, es decir A''B''C'' tiene sus lados paralelos a los del triángulo de Morley de ABC.