Proof of Lemma 3.
For an equilateral triangle ABC the envelope of its Wallace-Simson
lines is a tricuspidal hypocycloid whose vertices are the vertices
of an
equilateral triangle concentric with ABC, with sides parallel to
those
of ABC and whose size is 3/2 that of ABC.
The proof is easily obtained from the two following remarks:
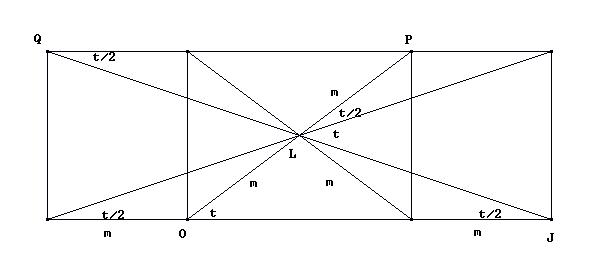 Figure 1
(a) If a rectangle with diagonal OP (diagonal length 2m) is enlarged
with two rectangles as the figure shows, then one has the indicated relations
between the angles.
Figure 1
(a) If a rectangle with diagonal OP (diagonal length 2m) is enlarged
with two rectangles as the figure shows, then one has the indicated relations
between the angles.
 Figure 2
Figure 2
(b) To the elements of Figure 1 one has added in
Figure 2 the circles U and V, with center at O and radii 2m and 3m, the
equilateral triangle ABC, the circle W with center at P and radius m, that
intersects QJ at T and L.
Then, since the angle PLT is 3t/2 (according
to Figure 1), we have that the angle SPT is 3t and thus T is a point of
the hypocycloid generated by W when it rolls inside V starting from the
position in which the center of W is on the line OA.
Since the angle STQ is 90º and ST is instantaneous
rotation radius of the circle W when it rolls inside V, the line TQ is
tangent at T to the hypocycloid. On the other hand since angle PQT is
t/2 we have (see Figure 3 below) that QT is the Wallace-Simson line
of P with respect to ABC. Thus the Wallace-Simson line of P with
respect to ABC is tangent to the hypocycloid at the point T. This proves
the lemma.
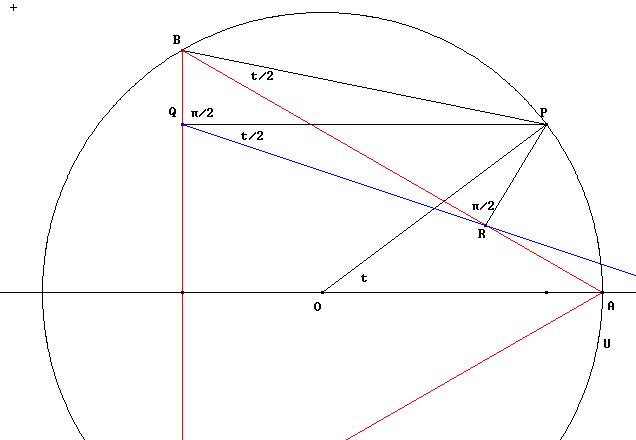 Figure 3
Since BPQR is a cyclic quadrilateral, the angles
PBR and PQR are equal. On the other hand the angle PBR, inscribed in the
circle U, is half the angle POA. Thus the Wallace-Simson line of P, i.e.
QR, is at an angle t/2 with PQ and so R coincides with the point T of the
previous figure 2.
Figure 3
Since BPQR is a cyclic quadrilateral, the angles
PBR and PQR are equal. On the other hand the angle PBR, inscribed in the
circle U, is half the angle POA. Thus the Wallace-Simson line of P, i.e.
QR, is at an angle t/2 with PQ and so R coincides with the point T of the
previous figure 2.
