More on Morley's triangles
There are some very beautiful configurations connected
with Morley's triangles that I have not seen explored before.
 Consider
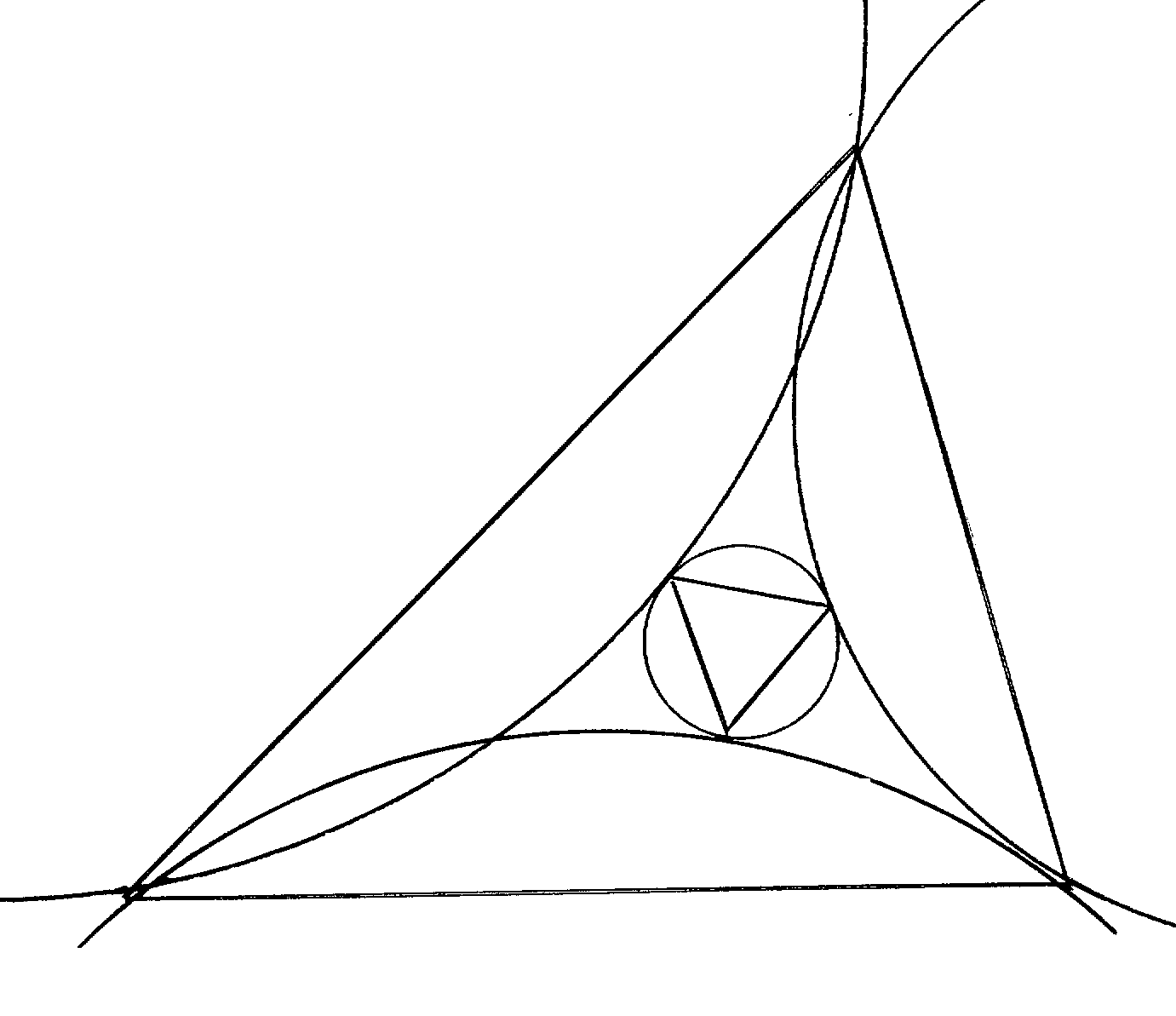
the classical Morley triangle MNP for ABC and its circumcircle K. Consider
the circle U passing through M, B, C and the corresponding ones, V passing
through N, C, A and W passing through P, A, B. Then K is tangent to U,
V, and W, the tangency points being M, N, and P respectively.
Consider
the classical Morley triangle MNP for ABC and its circumcircle K. Consider
the circle U passing through M, B, C and the corresponding ones, V passing
through N, C, A and W passing through P, A, B. Then K is tangent to U,
V, and W, the tangency points being M, N, and P respectively.
The same property is also valid for each one of the
other Morley triangles, i.e. in any case the circumcircle of the Morley
triangle is tangent to each one of the circles passing through one vertex
of the Morley triangle and the corresponding two vertices of the original
triangle ABC, the point of tangency being the vertex of the Morley triangle.
Here one can see the figure corresponding
to one of the non-classical Morley triangles.
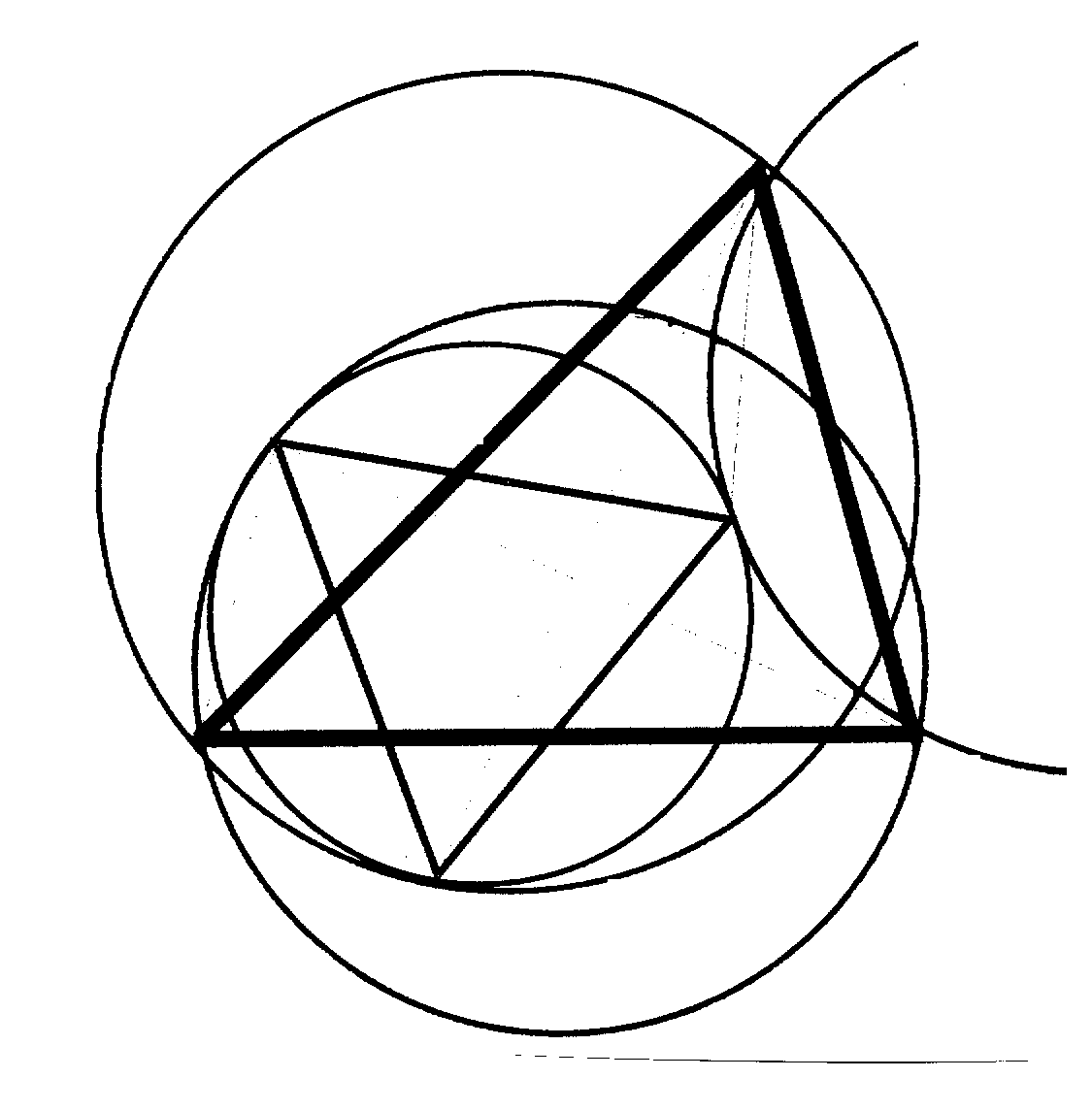
Consider
the classical Morley triangle MNP for ABC and its circumcircle K. Consider
the circle U passing through M, B, C and the corresponding ones, V passing
through N, C, A and W passing through P, A, B. Then K is tangent to U,
V, and W, the tangency points being M, N, and P respectively.