En
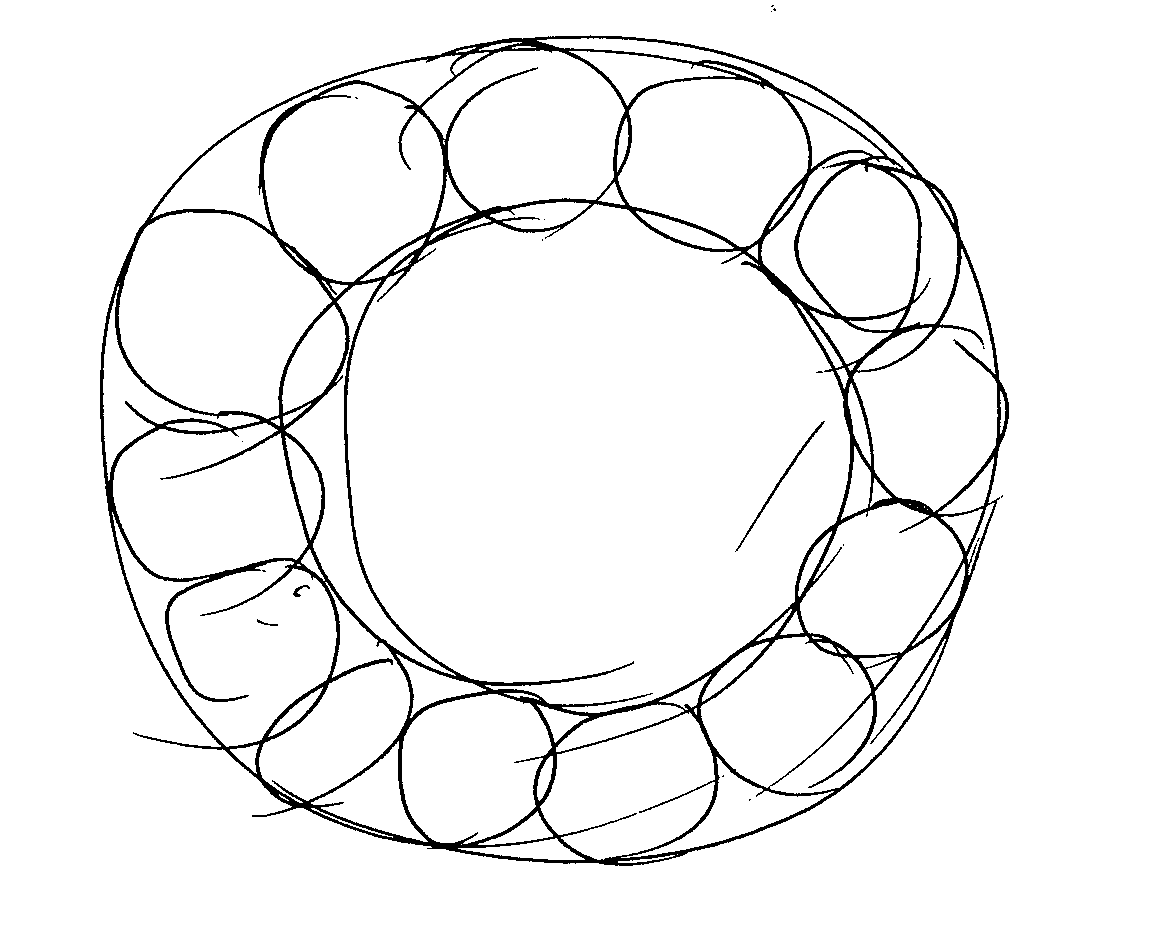
esta configuración la cadena se puede obviamente rotar. Se rota
y se deshace la transformación inicial. El teorema de Steiner queda
así demostrado.Demostración del teorema de las cadenas de círculos de Steiner
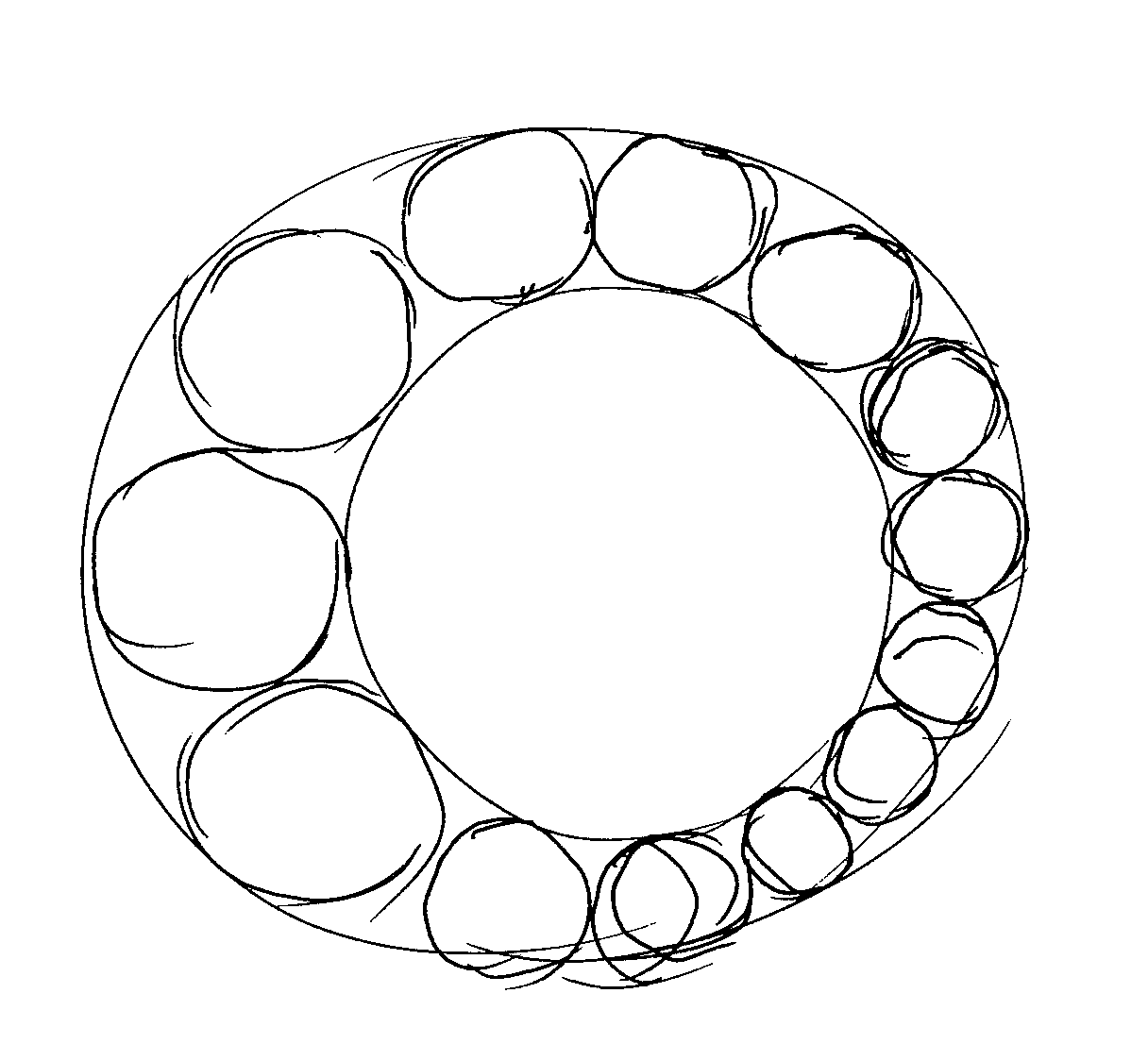Supongamos
que se tiene esta configuración. Por medio de la proyección
estereográfica (o de una inversión), los dos círculos
se hacen concéntricos, resultando una cadena de círculos
iguales, como en la figura siguiente.
En
esta configuración la cadena se puede obviamente rotar. Se rota
y se deshace la transformación inicial. El teorema de Steiner queda
así demostrado.