Sobre el teorema de Kariya
El teorema de Kariya es uno de los recuerdos más
persistentes que conservo de aquellos años en que la geometría
empezó a atraerme con fuerza. Yo debía de tener 13 ó
14 años. Mis hermanos hacían sus estudios para el ingreso
en Escuelas de Ingenieros. A través de ellos yo llegué a
tener acceso a los principales textos de geometría que entonces
se usaban en las academias de preparación para el ingreso en las
Escuelas de Ingenieros. Los que más me atrajeron fueron el tratado
de Rouché-Comberousse y la impresionante colección
de ejercicios de de geometría de F.G.-M.
Por cierto que solamente mucho más tarde, hace
unos pocos años, tuve ocasión de enterarme del significado
de esas abreviaturas tras las que se escondía el autor. Leyendo
el libro de H. Dörrie, 100 Great Problems of Elementary Mathematics.
Their History and Solution, Dover, New York, 1965, supe (página
359) que correspondían a Frère Gabriel-Marie.
Naturalmente que mis hermanos estudiaban otras cosas,
pero a mí me atrajo especialmente la geometría. ¿Por
qué? Tal vez había tenido ocasión de oir algo acerca
de la historia que se cuenta sobre la reinvención de una buena parte
de los Elementos de Euclides por Blas Pascal a sus 11 años, tal
vez encontraba todo aquello más afín a lo que me parecía
que yo era capaz de hacer, tal vez la magnífica introducción
a la geometría que a los 13 años había recibido de
mis profesores en los cursos iniciales de bachillerato Percha y Rodríguez
Sanjuán influyó muy decisivamente...
Yo sabía unos rudimentos de francés,
pero lo que no entendía bien lo adivinaba sin esfuerzo al adentrarme
con verdadero placer en aquellos textos. Creo que con esta motivación
aprendí más francés que en las clases regulares.
 El
libro de Rouché-Comberousse lo leía de modo bastante sistemático.
Los problemas del F.G.-M. me servían de ocupación salteada
en los muchos ratos de un ocio que recuerdo lleno de paz y de satisfacción
en medio del silencio de una clase solitaria en tardes de vacación.
Iba tratando por mi cuenta de resolver aquellos problemas y cuando después
de ocuparme en alguno un rato bastante largo no lograba dar con la respuesta
acudía al libro en que se ofrecía la solución y una
abundante información sobre los teoremas y problemas de más
envergadura.
El
libro de Rouché-Comberousse lo leía de modo bastante sistemático.
Los problemas del F.G.-M. me servían de ocupación salteada
en los muchos ratos de un ocio que recuerdo lleno de paz y de satisfacción
en medio del silencio de una clase solitaria en tardes de vacación.
Iba tratando por mi cuenta de resolver aquellos problemas y cuando después
de ocuparme en alguno un rato bastante largo no lograba dar con la respuesta
acudía al libro en que se ofrecía la solución y una
abundante información sobre los teoremas y problemas de más
envergadura.
De vez en cuando F.G.-M. ofrecía, en sus notas
informativas, resultados interesantes sin proporcionar pistas. Esto espoleaba
mi interés.
Los resultados alrededor del que allí se mencionaba
como teorema de Kariya (p. 550) me resultaron particularmente bonitos y
sugerentes:
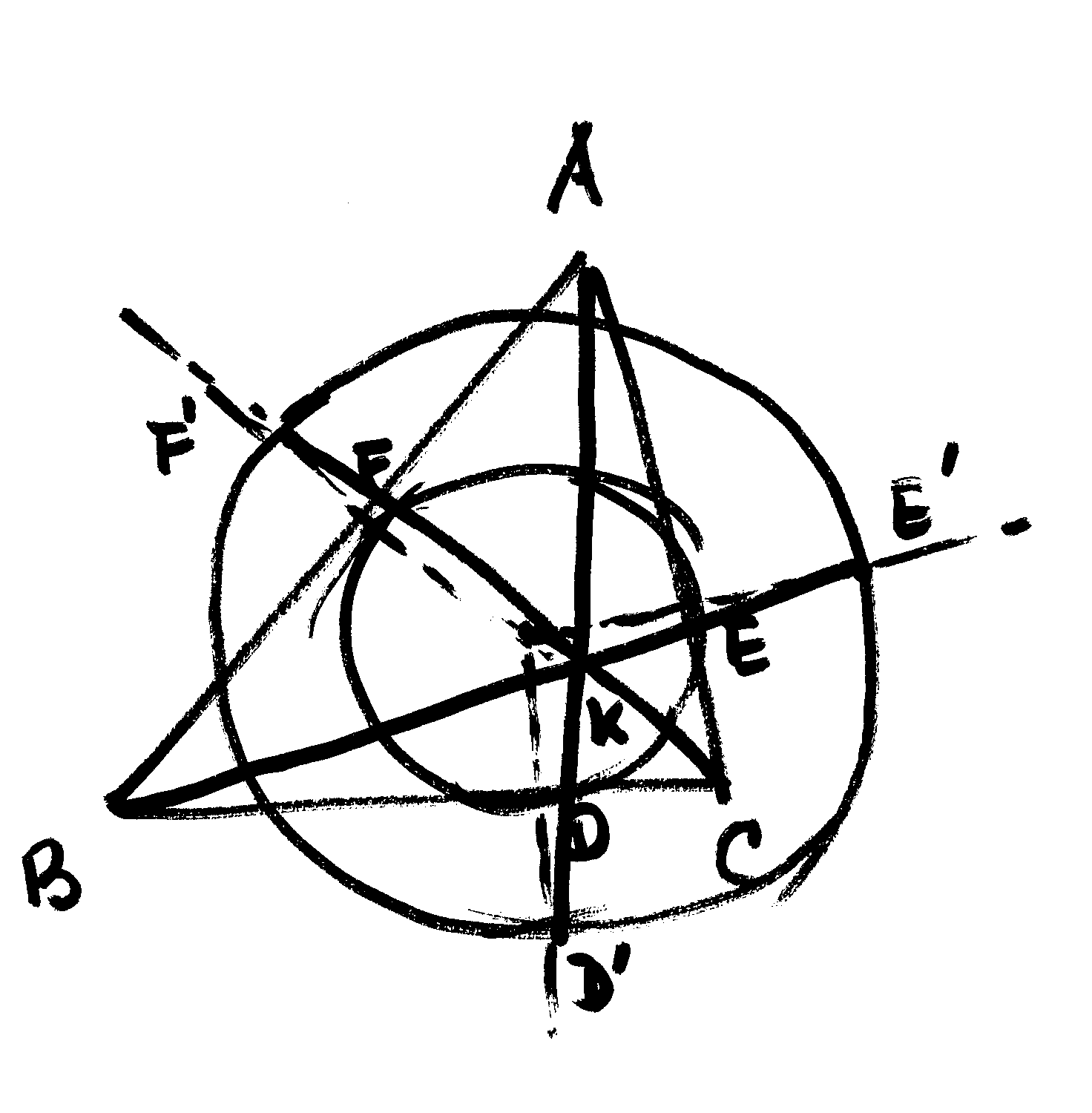 Se
tiene un triángulo arbitrario ABC. Se considera el círculo
inscrito de centro I y puntos de tangencia D con el lado a, E con el lado
b, F con el lado c. Se señala una longitud l y se toman sendos puntos
D', E', F' sobre las rectas ID, IE, IF, a distancia l de I. Entonces AD',
BE' y CF' concurren en un punto K (punto de Kariya). Cuando l varía
entonces K se mueve sobre una hipérbola equilátera que pasa
por A, B, C, el ortocentro H y el incentro I.
Se
tiene un triángulo arbitrario ABC. Se considera el círculo
inscrito de centro I y puntos de tangencia D con el lado a, E con el lado
b, F con el lado c. Se señala una longitud l y se toman sendos puntos
D', E', F' sobre las rectas ID, IE, IF, a distancia l de I. Entonces AD',
BE' y CF' concurren en un punto K (punto de Kariya). Cuando l varía
entonces K se mueve sobre una hipérbola equilátera que pasa
por A, B, C, el ortocentro H y el incentro I.
F.G.-M ofrecía mucha información, que
se puede ver aquí. La demostración
de la concurrencia de las tres rectas se podía deducir del teorema
de Ceva, pero lo demás... me parecía extraño, misterioso
y atrayente. Muchas vueltas tuve que darle por mi cuenta ya que allí
no aparecían pistas suficientes para mí... Hasta que por
fin me vino la luz que me aclaró éste y otros muchos misterios
parecidos. La aparición de una hipérbola parecía apuntar
hacia la forma en que una cónica se genera por intersección
de dos haces de rectas proyectivos.
Era claro que las tres series de puntos formados por
{I, D, D', infinito}, {I, E, E', infinito}, {I, F, F', infinito} se obtenían
una de la otra por un mero giro. Así, al proyectar la primera desde
A y la segunda desde B originaban por intersección de rayos homólogos
una cónica que pasaba por A, B, C, I, H y por tanto coincidía
con la cónica obtenida de modo semejante por proyección desde
A y C. Que la cónica era una hipérbola equilátera
era claro a partir de la caracterización de las hipérbolas
equiláteras. Una cónica que pasa por tres puntos A, B, C,
es una hipérbola equilátera si y sólo si pasa también
por el ortocentro del triángulo ABC.
Pero una vez que se tiene esta idea, unos cuantos teoremas
semejantes están ya a la mano. Su demostración es análoga
a la anterior.
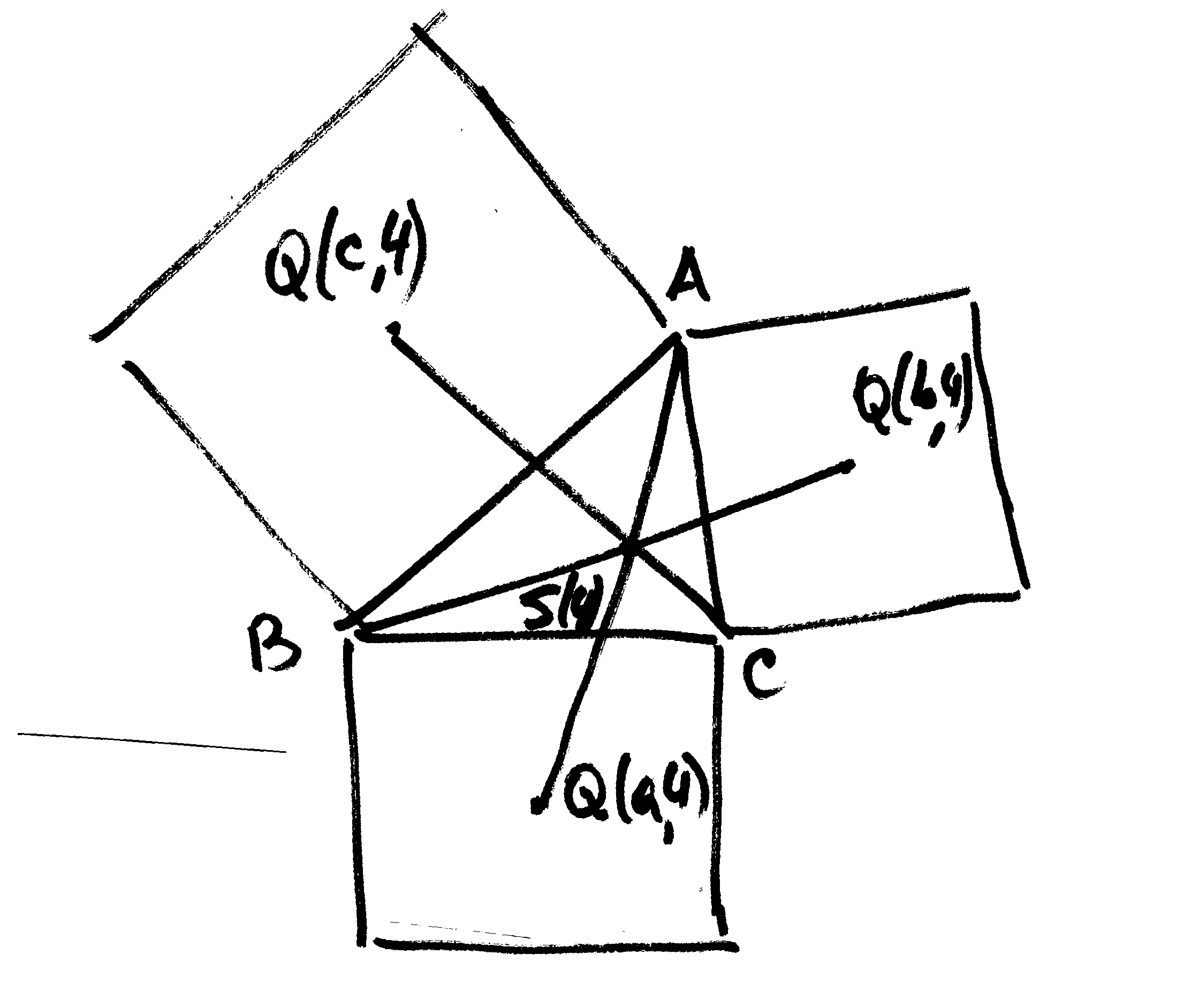 (1)
Sea ABC un triángulo arbitrario. Sobre cada lado a, b c, se construye
hacia el exterior (o bien hacia el lado del triángulo), un polígono
regular de n lados que denominaremos P(a,n), P(b,n), P(c,n). Sea Q(x,n)
el centro de P(x,n). Entonces las rectas AQ(a,n), BQ(b,n), CQ(c,n) concurren
en un punto que llamaremos S(n). Cuando n varía S(n) se encuentra
sobre la hipérbola equilátera que pasa por A, B, C, H (el
ortocentro de ABC), G (el centro de gravedad de ABC) y F (el punto de Fermat
de ABC, que en realidad coincide con S(6)).
(1)
Sea ABC un triángulo arbitrario. Sobre cada lado a, b c, se construye
hacia el exterior (o bien hacia el lado del triángulo), un polígono
regular de n lados que denominaremos P(a,n), P(b,n), P(c,n). Sea Q(x,n)
el centro de P(x,n). Entonces las rectas AQ(a,n), BQ(b,n), CQ(c,n) concurren
en un punto que llamaremos S(n). Cuando n varía S(n) se encuentra
sobre la hipérbola equilátera que pasa por A, B, C, H (el
ortocentro de ABC), G (el centro de gravedad de ABC) y F (el punto de Fermat
de ABC, que en realidad coincide con S(6)).
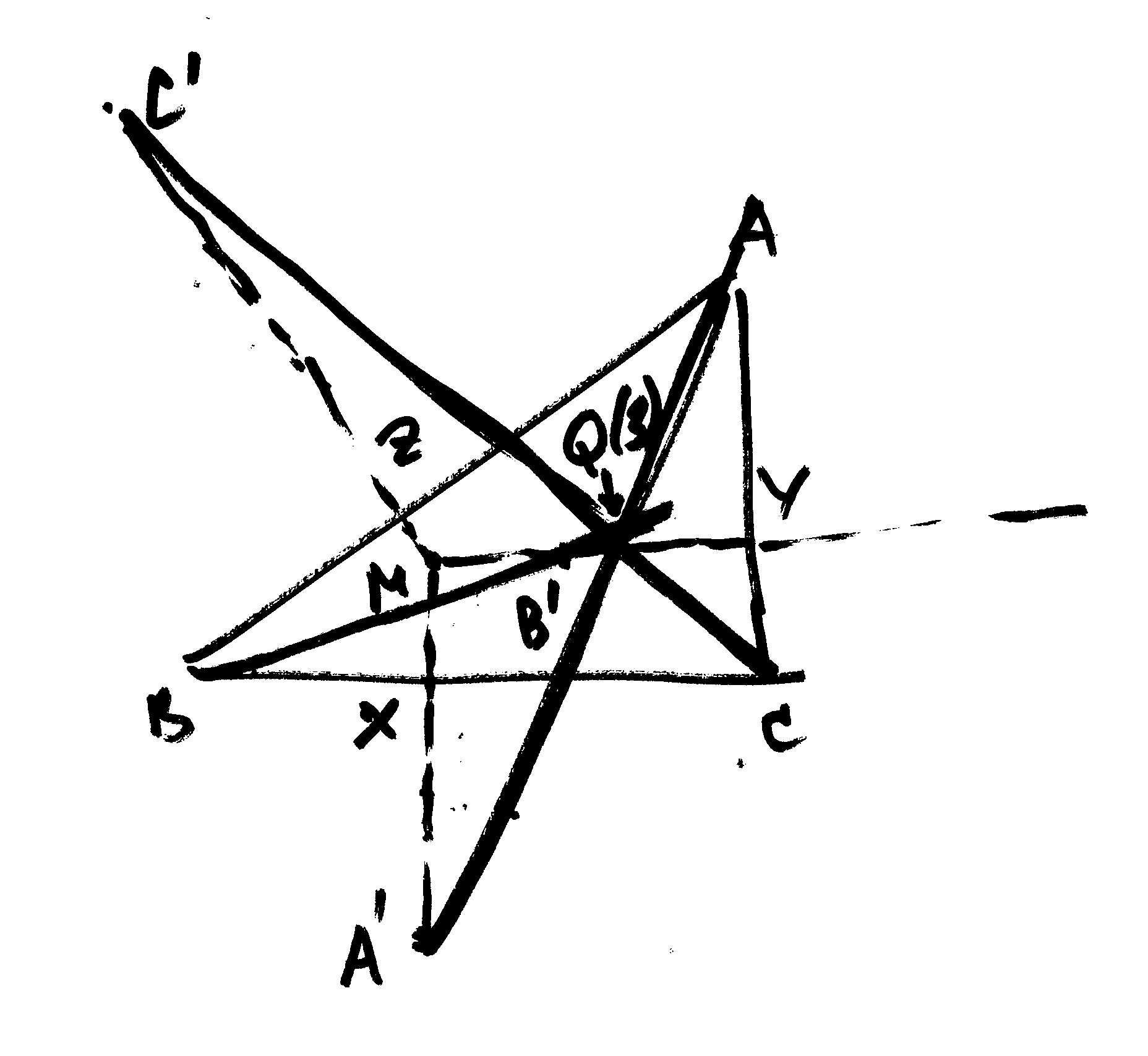 (2)
Sea ABC un triángulo arbitrario. Sea M un punto de su plano distinto
del ortocentro H de ABC y no situado sobre ninguno de los lados. Sean X,
Y, Z, las proyecciones de M sobre los lados a, b, c. Supongamos que AX,
BY, CZ concurren en P. Sea k un número real. Sobre MX, MY, MZ se
toman sendos puntos A', B', C' tales que MA'=k/MX, MB'=k/MY, MC'=k/MZ.
Entonces AA', BB', CC' concurren en un punto Q(k). Cuando k varía
Q(k) recorre una hipérbola equilátera que pasa por A, B,
C, P y H.
(2)
Sea ABC un triángulo arbitrario. Sea M un punto de su plano distinto
del ortocentro H de ABC y no situado sobre ninguno de los lados. Sean X,
Y, Z, las proyecciones de M sobre los lados a, b, c. Supongamos que AX,
BY, CZ concurren en P. Sea k un número real. Sobre MX, MY, MZ se
toman sendos puntos A', B', C' tales que MA'=k/MX, MB'=k/MY, MC'=k/MZ.
Entonces AA', BB', CC' concurren en un punto Q(k). Cuando k varía
Q(k) recorre una hipérbola equilátera que pasa por A, B,
C, P y H.
Es claro que el teorema anterior es una generalización
del teorema de Kariya de arriba, que se obtiene de él cuando M es
el incentro de ABC. Cuando M coincide con el centro de una de las tres
circunferencias exinscritas se obtiene una hipérbola análoga
a la del teorema de Kariya.
La hipérbola que ha resultado en el teorema
de Kariya es muy interesante. Su transformada isogonal es precisamente
la recta de Euler.
El conjunto de puntos M tales que AX, BY y CZ concurren
es una cúbica que tiene conexiones curiosísimas con algunos
de los principales personajes del triángulo. La veremos más
a fondo.
Todos estos resultados me llenaban de admiración
al contemplar la belleza y riqueza de las estructuras geométricas
que se podían presentir.
 El
libro de Rouché-Comberousse lo leía de modo bastante sistemático.
Los problemas del F.G.-M. me servían de ocupación salteada
en los muchos ratos de un ocio que recuerdo lleno de paz y de satisfacción
en medio del silencio de una clase solitaria en tardes de vacación.
Iba tratando por mi cuenta de resolver aquellos problemas y cuando después
de ocuparme en alguno un rato bastante largo no lograba dar con la respuesta
acudía al libro en que se ofrecía la solución y una
abundante información sobre los teoremas y problemas de más
envergadura.
El
libro de Rouché-Comberousse lo leía de modo bastante sistemático.
Los problemas del F.G.-M. me servían de ocupación salteada
en los muchos ratos de un ocio que recuerdo lleno de paz y de satisfacción
en medio del silencio de una clase solitaria en tardes de vacación.
Iba tratando por mi cuenta de resolver aquellos problemas y cuando después
de ocuparme en alguno un rato bastante largo no lograba dar con la respuesta
acudía al libro en que se ofrecía la solución y una
abundante información sobre los teoremas y problemas de más
envergadura.
 Se
tiene un triángulo arbitrario ABC. Se considera el círculo
inscrito de centro I y puntos de tangencia D con el lado a, E con el lado
b, F con el lado c. Se señala una longitud l y se toman sendos puntos
D', E', F' sobre las rectas ID, IE, IF, a distancia l de I. Entonces AD',
BE' y CF' concurren en un punto K (punto de Kariya). Cuando l varía
entonces K se mueve sobre una hipérbola equilátera que pasa
por A, B, C, el ortocentro H y el incentro I.
Se
tiene un triángulo arbitrario ABC. Se considera el círculo
inscrito de centro I y puntos de tangencia D con el lado a, E con el lado
b, F con el lado c. Se señala una longitud l y se toman sendos puntos
D', E', F' sobre las rectas ID, IE, IF, a distancia l de I. Entonces AD',
BE' y CF' concurren en un punto K (punto de Kariya). Cuando l varía
entonces K se mueve sobre una hipérbola equilátera que pasa
por A, B, C, el ortocentro H y el incentro I.
 (1)
Sea ABC un triángulo arbitrario. Sobre cada lado a, b c, se construye
hacia el exterior (o bien hacia el lado del triángulo), un polígono
regular de n lados que denominaremos P(a,n), P(b,n), P(c,n). Sea Q(x,n)
el centro de P(x,n). Entonces las rectas AQ(a,n), BQ(b,n), CQ(c,n) concurren
en un punto que llamaremos S(n). Cuando n varía S(n) se encuentra
sobre la hipérbola equilátera que pasa por A, B, C, H (el
ortocentro de ABC), G (el centro de gravedad de ABC) y F (el punto de Fermat
de ABC, que en realidad coincide con S(6)).
(1)
Sea ABC un triángulo arbitrario. Sobre cada lado a, b c, se construye
hacia el exterior (o bien hacia el lado del triángulo), un polígono
regular de n lados que denominaremos P(a,n), P(b,n), P(c,n). Sea Q(x,n)
el centro de P(x,n). Entonces las rectas AQ(a,n), BQ(b,n), CQ(c,n) concurren
en un punto que llamaremos S(n). Cuando n varía S(n) se encuentra
sobre la hipérbola equilátera que pasa por A, B, C, H (el
ortocentro de ABC), G (el centro de gravedad de ABC) y F (el punto de Fermat
de ABC, que en realidad coincide con S(6)).
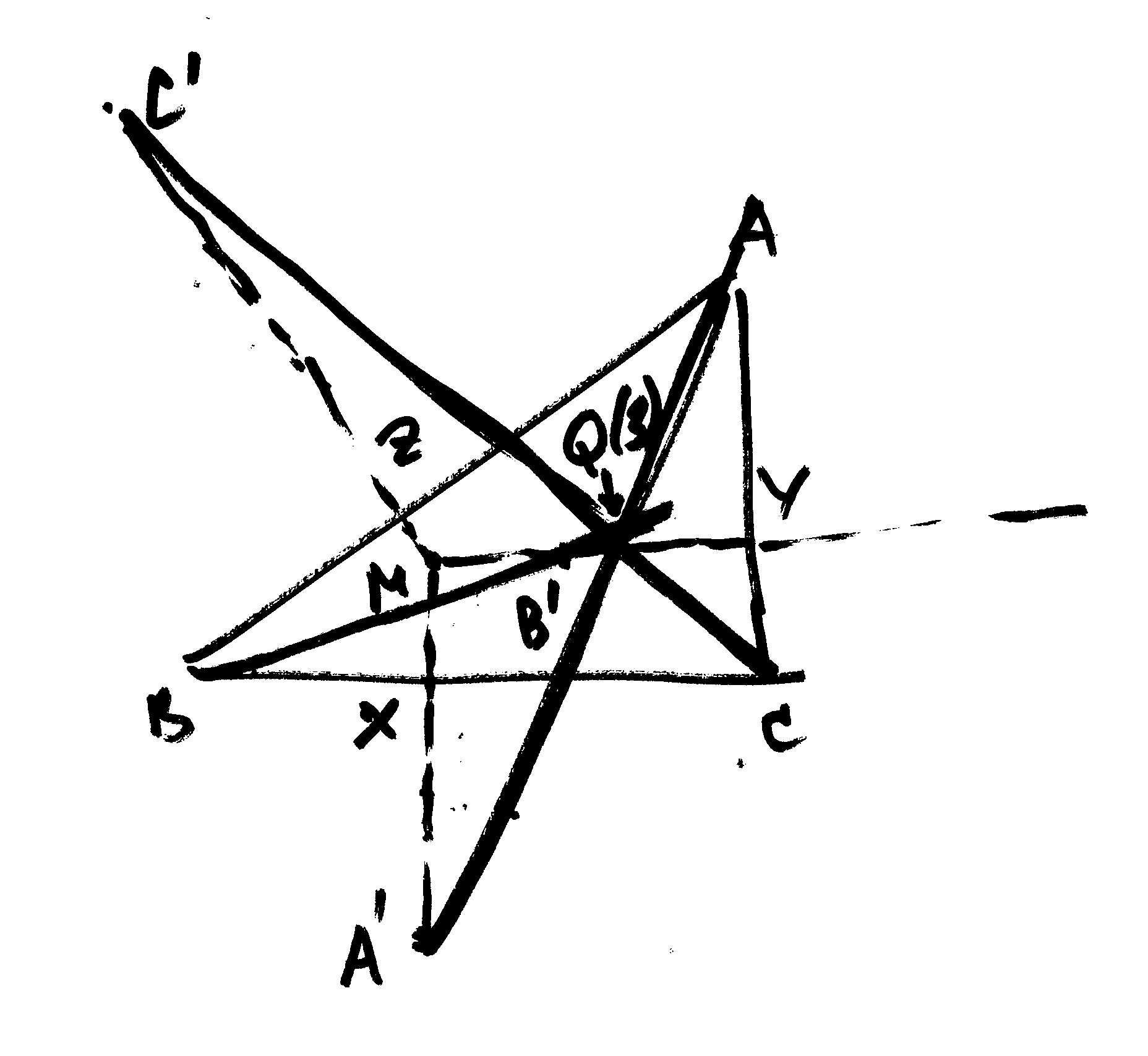 (2)
Sea ABC un triángulo arbitrario. Sea M un punto de su plano distinto
del ortocentro H de ABC y no situado sobre ninguno de los lados. Sean X,
Y, Z, las proyecciones de M sobre los lados a, b, c. Supongamos que AX,
BY, CZ concurren en P. Sea k un número real. Sobre MX, MY, MZ se
toman sendos puntos A', B', C' tales que MA'=k/MX, MB'=k/MY, MC'=k/MZ.
Entonces AA', BB', CC' concurren en un punto Q(k). Cuando k varía
Q(k) recorre una hipérbola equilátera que pasa por A, B,
C, P y H.
(2)
Sea ABC un triángulo arbitrario. Sea M un punto de su plano distinto
del ortocentro H de ABC y no situado sobre ninguno de los lados. Sean X,
Y, Z, las proyecciones de M sobre los lados a, b, c. Supongamos que AX,
BY, CZ concurren en P. Sea k un número real. Sobre MX, MY, MZ se
toman sendos puntos A', B', C' tales que MA'=k/MX, MB'=k/MY, MC'=k/MZ.
Entonces AA', BB', CC' concurren en un punto Q(k). Cuando k varía
Q(k) recorre una hipérbola equilátera que pasa por A, B,
C, P y H.