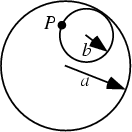
| (1) |
| (2) |
| x | = | ||
| = | 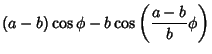 |
(3) | |
| y | = | ||
| = | 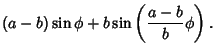 |
(4) |
If x(0)=a instead so the first point is at maximum radius (on the Circle), then the equations of the hypocycloid are
| x | = | 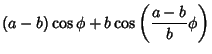 |
(5) |
| y | = |  |
(6) |
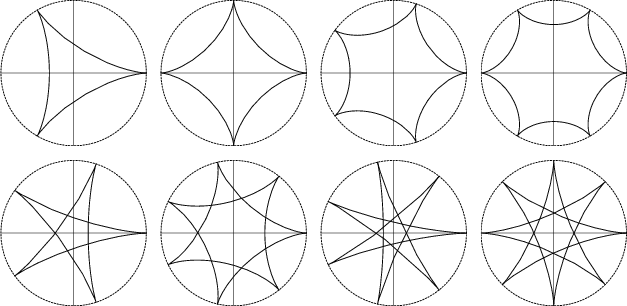
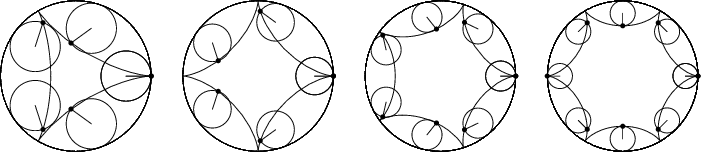
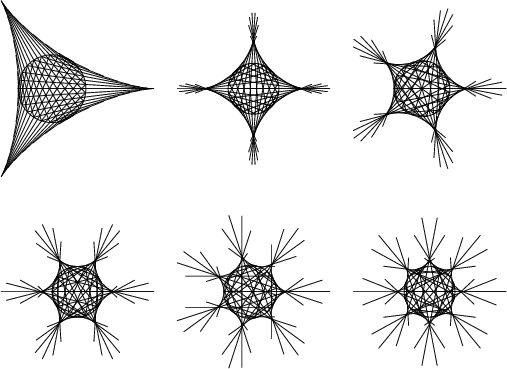
An n-cusped non-self-intersecting hypocycloid has a/b=n. A 2-cusped hypocycloid is a Line Segment (Steinhaus 1983, p. 145), as can be seen by setting a=b in equations (3) and (4) and noting that the equations simplify to
| x | = | (7) | |
| y | = | 0. | (8) |
A 3-cusped hypocycloid is called a Deltoid
or Tricuspoid,
and a 4-cusped hypocycloid is called anAstroid.
If a/b is rational, the curve closes
on itself and has b cusps. If a/b
is Irrational,
the curve never closes and fills the entire interior of the Circle.
Let r be the radial distance from
a fixed point. For Radius
of Torsion![]() and Arc
Lengths, a hypocycloid can given by
the equation
and Arc
Lengths, a hypocycloid can given by
the equation
| (9) |
| (10) |
| (11) |
The Arc Length of the hypocycloid can be computed as follows
| x' | = | 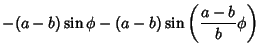 |
|
| = | ![$\displaystyle (a-b)\left[{\sin\phi+\sin\left({{a-b\over b}\phi}\right)}\right]$](himg1877.gif) |
(12) | |
| y' | = | 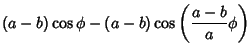 |
|
| = | ![$\displaystyle (a-b)\left[{\cos\phi-\cos\left({{a-b\over b}\phi}\right)}\right]$](himg1879.gif) |
(13) |
| (14) |
so
| ds | = | 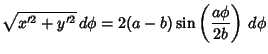 |
(15) |
for ![]() .
Integrating,
.
Integrating,
| = | ![$\displaystyle \int_0^\phi ds=2(a-b)\left[{-{2b\over a}\cos\left({a\phi\over 2b}\right)}\right]_0^\phi$](himg1887.gif) |
||
| = | ![$\displaystyle {4b(a-b)\over a}\left[{-\cos\left({{a\over 2b}\phi}\right)+1}\right]$](himg1888.gif) |
||
| = | 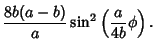 |
(16) |
The length of a single cusp is then
| (17) |
| x | = | (18) | |
| y | = | (19) |
and
| (20) |
| xy'-yx' | = | \left[{\sin \phi+\sin\left({{a-b\over b} \phi}\right)}\right]$](himg1895.gif) |
|
\left[{\cos \phi-\cos\left({{a-b\over b} \phi}\right)}\right]$](himg1896.gif) |
|||
| = | 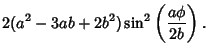 |
(21) |
The Area of one cusp is then
| A | = | 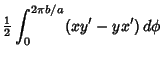 |
|
| = | ![$\displaystyle (a^2-3ab+2b^2)\left[{at-b\sin\left({at\over b}\right)\over 2a}\right]^{2\pi b/a}_a$](himg1899.gif) |
||
| = | ![$\displaystyle (a^2-3ab+2b^2)\left[{a\left({2\pi{b\over a}}\right)\over 2a}\right]$](himg1900.gif) |
||
| = | 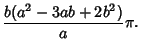 |
(22) |
If n=a/b is rational,
then after n cusps,
| An | = | 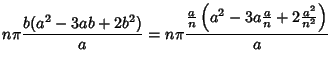 |
|
| = | 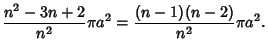 |
(23) |
The equation of the hypocycloid can be put in a form which is useful
in the solution of Calculus
of Variations problems with radial symmetry. Consider the case ![]() ,
then
,
then
| r2 | = | x2+y2 | |
| = | 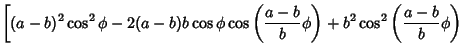 |
||
![$\displaystyle \mathop{+} \left.{(a-b)^2\sin^2\phi+2(a-b)b\sin\phi\sin\left({{a-b\over b}\phi}\right)+b^2\sin^2\left({{a-b\over b}\phi}\right)}\right]$](himg1905.gif) |
|||
| = | ![$\displaystyle \left\{{(a-b)^2+b^2-2(a-b)b}\left[{\cos\phi\cos\left({{a-b\over b}\phi}\right)-\sin\phi\sin\left({{a-b\over b}\phi}\right)}\right]\right\}$](himg1906.gif) |
||
| = | (24) |
But ![]() ,
so
,
so ![]() ,
which gives
,
which gives
| (a-b)2+b2 | = | ||
| = | |||
| = | |||
| = | (25) | ||
| 2(a-b)b | = | ||
| = | (26) |
Now let
| (27) |
| (28) |
| (29) |
| r2 | = | ||
| = | (30) |
The Polar
Angle is
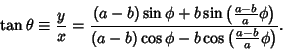 |
(31) |
| b | = | (32) | |
| a-b | = | (33) | |
| = | (34) |
so
| = | 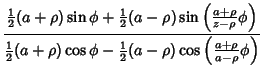 |
||
| = | 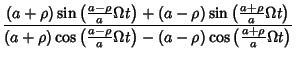 |
||
| = | ![$\displaystyle {a\left[{\sin\left({{a-\rho\over a}\Omega t}\right)+\sin\left({{a......ho\over a} \Omega t}\right)+\cos\left({{a+\rho\over a}\Omega t}\right)}\right]}$](himg1929.gif) |
||
| = | 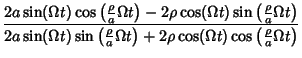 |
||
| = | 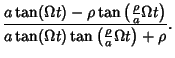 |
(35) |
Computing
| = | ![$\displaystyle {\left[{a\tan(\Omega t)-\rho\tan\left({{\rho\over a}\Omega t}\rig......{{\rho\over a}\Omega t}\right)}\right]\tan\left({{\rho\over a}\Omega t}\right)}$](himg1933.gif) |
||
| = | ![$\displaystyle {a\tan(\Omega t)\left[{1+\tan^2\left({{\rho\over a}\Omega t}\right)}\right]\over\rho\left[{1+\tan^2\left({{\rho\over a}\Omega t}\right)}\right]}$](himg1934.gif) |
||
| = | (36) |
then gives
| (37) |
| = | ![$\displaystyle \tan^{-1}\left[{{a\over\rho}\tan\left({{a\over a-\rho}\phi}\right)}\right]-{\rho\over a}{a\over a-\rho} \phi$](himg1937.gif) |
||
| = | ![$\displaystyle \tan^{-1}\left[{{a\over\rho}\tan\left({{a\over a-\rho}\phi}\right)}\right]-{\rho\over a-\rho}\phi.$](himg1938.gif) |
(38) |
This form is useful in the solution of the Sphere
with Tunnel problem, which is the generalization of theBrachistochrone
Problem, to find the shape of a tunnel drilled through a Sphere
(with
gravity![]() varying according to Gauss's
law for gravitation
varying according to Gauss's
law for gravitation![]() ) such
that the travel time between two points on the surface of the Sphere
under the force of
gravity
) such
that the travel time between two points on the surface of the Sphere
under the force of
gravity![]() is minimized.
is minimized.
See also Astroid, Cycloid, Deltoid, Epicycloid
References
Bogomolny, A. ``Cycloids.'' http://www.cut-the-knot.com/pythagoras/cycloids.html.
Kreyszig, E. Differential Geometry. New York: Dover, 1991.
Lawrence, J. D. A Catalog of Special Plane Curves. New York: Dover, pp. 171-173, 1972.
Lee, X. ``Epicycloid and Hypocycloid.'' http://www.best.com/~xah/SpecialPlaneCurves_dir/EpiHypocycloid_dir/epiHypocycloid.html.
MacTutor History of Mathematics Archive. ``Hypocycloid.'' http://www-groups.dcs.st-and.ac.uk/~history/Curves/Hypocycloid.html.
Madachy, J. S. Madachy's Mathematical Recreations. New York: Dover, pp. 225-231, 1979.
Steinhaus, H. Mathematical Snapshots, 3rd American ed. New York: Oxford University Press, 1983.
Wagon, S. Mathematica in Action. New York: W. H. Freeman, pp. 50-52, 1991.
Yates, R. C. ``Epi- and Hypo-Cycloids.'' A
Handbook on Curves and Their Properties. Ann Arbor, MI:
J. W. Edwards, pp. 81-85, 1952.
© 1996-9 Eric W. Weisstein