 |
|
The derivative of a function
represents an infinitesimal change in the function with respect to whatever
parameters it may have. The ``simple'' derivative of a function 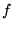 with respect to
with respect to 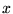 is denoted either
is denoted either 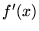 or
or
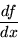 |
(1) |
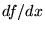 ).
When derivatives are taken with respect to time, they are often denoted
using Newton's ).
When derivatives are taken with respect to time, they are often denoted
using Newton's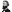 overdot notation
for fluxions,
overdot notation
for fluxions,
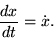 |
(2) |
The derivative of a function 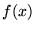 with respect to the variable
with respect to the variable 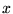 is defined as
is defined as
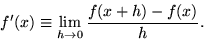 |
(3) |
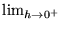 and
and 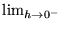 must exist and be equal, so the
function
must be continuous. However, continuity is a necessary
but not sufficient
condition for differentiability. Since some discontinuous
functions can be integrated, in a sense there are ``more'' functions which
can be integrated than differentiated. In a letter to Stieltjes, Hermite
must exist and be equal, so the
function
must be continuous. However, continuity is a necessary
but not sufficient
condition for differentiability. Since some discontinuous
functions can be integrated, in a sense there are ``more'' functions which
can be integrated than differentiated. In a letter to Stieltjes, Hermite wrote, ``I recoil with dismay and horror at this lamentable plague of functions
which do not have derivatives.''
wrote, ``I recoil with dismay and horror at this lamentable plague of functions
which do not have derivatives.''
A 3-D generalization of the derivative to an arbitrary direction is
known as the directional
derivative. In general, derivatives are mathematical objects which
exist between smooth functions on manifolds. In this formalism, derivatives
are usually assembled into ``tangent
maps.''
Simple derivatives of some simple functions follow.
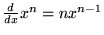 |
(4) |
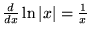 |
(5) |
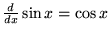 |
(6) |
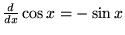 |
(7) |
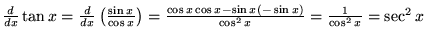 |
(8) |
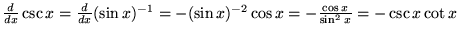 |
(9) |
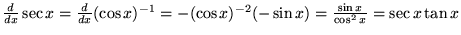 |
(10) |
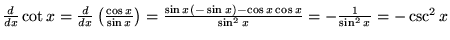 |
(11) |
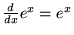 |
(12) |
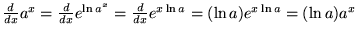 |
(13) |
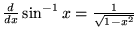 |
(14) |
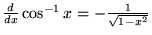 |
(15) |
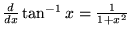 |
(16) |
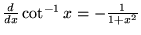 |
(17) |
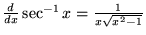 |
(18) |
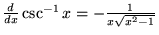 |
(19) |
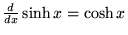 |
(20) |
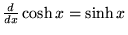 |
(21) |
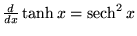 |
(22) |
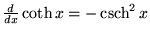 |
(23) |
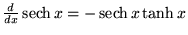 |
(24) |
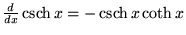 |
(25) |
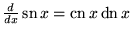 |
(26) |
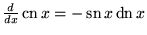 |
(27) |
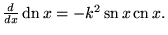 |
(28) |
where 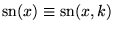 , , 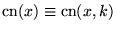 ,
etc. are Jacobi
elliptic functions, and the product
rule and quotient
rule have been used extensively to expand the derivatives. ,
etc. are Jacobi
elliptic functions, and the product
rule and quotient
rule have been used extensively to expand the derivatives.
Derivatives of sums are equal to the sum of derivatives so that
![\begin{displaymath}[f(x)+\ldots+h(x)]'=f'(x)+\ldots+h'(x). \end{displaymath}](d1img1049.gif) |
(29) |
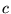 is a constant,
is a constant,
![\begin{displaymath} {d\over dx}[c f(x)]=cf'(x).\end{displaymath}](d1img1050.gif) |
(30) |
![\begin{displaymath} {d\over dx}[f(x)g(x)] = f(x)g'(x)+f'(x)g(x),\end{displaymath}](d1img1051.gif) |
(31) |
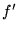 denotes the derivative
of
denotes the derivative
of 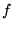 with respect to
with respect to 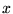 .
This derivative rule can be applied iteratively to yield derivate rules
for products of three or more functions, for example, .
This derivative rule can be applied iteratively to yield derivate rules
for products of three or more functions, for example,
The quotient
rule
![\begin{displaymath} {d\over dx} \left[{f(x)\over g(x)}\right]= {g(x)f'(x)-f(x)g'(x)\over [g(x)]^2}\end{displaymath}](d1img1056.gif) |
(33) |
Miscellaneous other derivative identities include
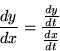 |
(34) |
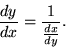 |
(35) |
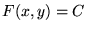 ,
where ,
where 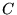 is a constant, then
is a constant, then
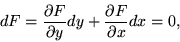 |
(36) |
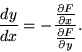 |
(37) |
A vector derivative of a vector function
![\begin{displaymath} \mathbf{X}(t) \equiv\left[{\matrix{x_1(t)\cr x_2(t)\cr \vdots\cr x_k(t)\cr}}\right]\end{displaymath}](d1img1062.gif) |
(38) |
![\begin{displaymath} {d\mathbf{X}\over dt} = \left[{\matrix{{dx_1\over dt}\cr {dx_2\over dt}\cr \vdots\cr {dx_k\over dt}\cr}}\right].\end{displaymath}](d1img1063.gif) |
(39) |
 Blancmange
Function, Carathéodory
Derivative, Chain
Rule, Comma
Derivative, Convective
Derivative, Covariant
Derivative, Directional
Derivative,
Euler-Lagrange
Derivative, Fluxion,
Fractional
Calculus, Fréchet
Derivative, Lagrangian
Derivative, Lie
Derivative, Logarithmic
Derivative, Pincherle
Derivative, Power
Rule, Product
Rule, q-Series,
Quotient Rule,
Schwarzian
Derivative, Semicolon
Derivative, Weierstrass
Function Blancmange
Function, Carathéodory
Derivative, Chain
Rule, Comma
Derivative, Convective
Derivative, Covariant
Derivative, Directional
Derivative,
Euler-Lagrange
Derivative, Fluxion,
Fractional
Calculus, Fréchet
Derivative, Lagrangian
Derivative, Lie
Derivative, Logarithmic
Derivative, Pincherle
Derivative, Power
Rule, Product
Rule, q-Series,
Quotient Rule,
Schwarzian
Derivative, Semicolon
Derivative, Weierstrass
Function

References
Abramowitz, M. and Stegun, C. A. (Eds.). Handbook
of Mathematical Functions with Formulas, Graphs, and Mathematical Tables,
9th printing. New York: Dover, p. 11, 1972.
Anton, H. Calculus:
A New Horizon, 6th ed. New York: Wiley, 1999.
Beyer, W. H. ``Derivatives.'' CRC
Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC
Press, pp. 229-232, 1987.
Griewank, A. Principles
and Techniques of Algorithmic Differentiation. Philadelphia,
PA: SIAM, 2000.
© 1996-2000 Eric W. Weisstein and Wolfram Research,
Inc.
Sponsored by Wolfram Research, Inc., makers of Mathematica
|
