The aim of this paper is to present and discuss generalities of Teaching Practice and Primary Teacher Education in Hungary and some specialities performed at the Department of Mathematics of the Budapest Teachers’ Training College (Independent institute until January 2000, a faculty of Eotvos University Budapest after that date).

It is hoped that this paper can give an insight into the traditions and present practice of teacher training in mathematics in Hungary, a country where mathematics and mathematics education have always represented vital aspects of cultural life.

1. INTRODUCTION
Teacher Education in Hungary has three different kinds of institutions.

Universities train prospective teachers of different subjects (like mathematics) for the education of 10-18 years olds (one or two subjects). It is a type of 5 years long education which ends with an oral State Exaimination and a written thesis defended also at the State Examination.

Teacher Training Colleges train prospective teachers of different subjects (like mathematics) for the education of 10-14 years olds (one or two subjects). It is a type of 4 years long education which ends with an oral State Examination and a written thesis defended also at the State Examination.

Teacher Training Colleges train prospective teachers for the education of all subjects of 6-10 year olds (primary education) and one subject (like mathematics) of 10-12 year olds. It is a type of 4 years long education which ends with an oral State Examination and a written thesis defended also at the State Examination.

My task is now to focus on a small but, in my opinion an important slice of this "cake", the primary mathematics education.
I would like to concentrate on the possibilities of pre-service training on this domain. Precisely on the topics of the kind of organisations, activities and teamwork of a pair of primary mentor teacher and a university researcher-educator (college teacher) can help their students to learn the state of art of the practical work of a primary teacher. How can they integrate the activities into the theoretical and practical knowledge and increase the efficiency of the university education?

In this complex historical perspective, primary teachers’ preparation in mathematics had been a crucial pont since 1869 when primary teachers were prepared by a specialized, well-considered secondary school established by the law of the State. Since 1959 primary teachers are trained at college level 3 years after finishing a secondary school which ends with a maturity examination and since 1995 following the successful experiment of the Budapest Teachers Training College a 4-year long, 3200 hours (45 min) university level education.

Using a German tradition the Institutes have been associated with primary schools in order to create the possibility for the undergraduate students to teach and gradually improve their practical teaching abilities.
Actually, the practical teaching was always an important part of the training of primary teachers.

Budapest Teachers’ Training College (BTTC) is one of the third type institutions in Hungary (described above).

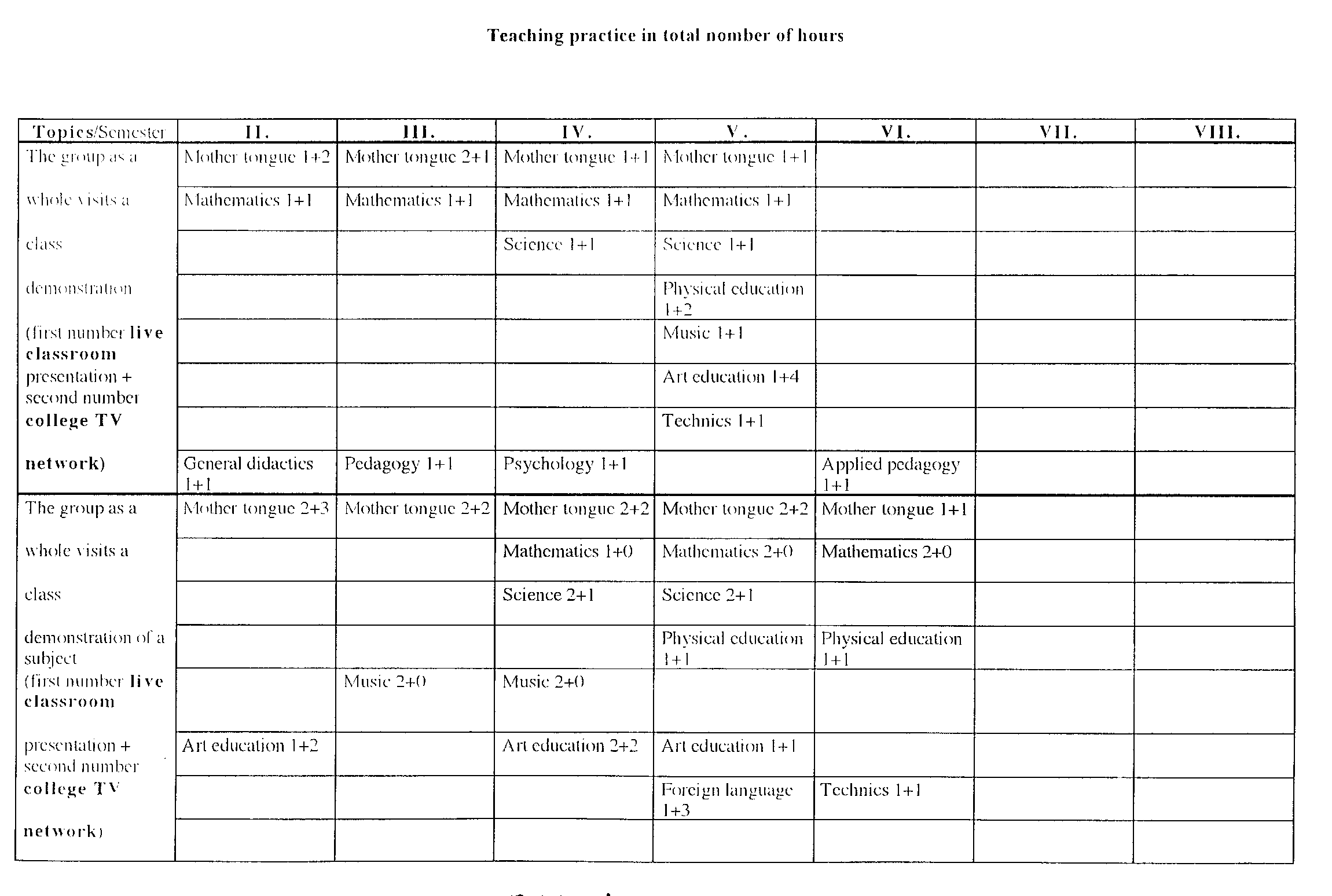
The system of mathematics instructions and school practice at BTTC is as schematically indicated in the following three tables:
(The tables can be enlarged by opening them in a new window)

TABLE 1

TABLE 2

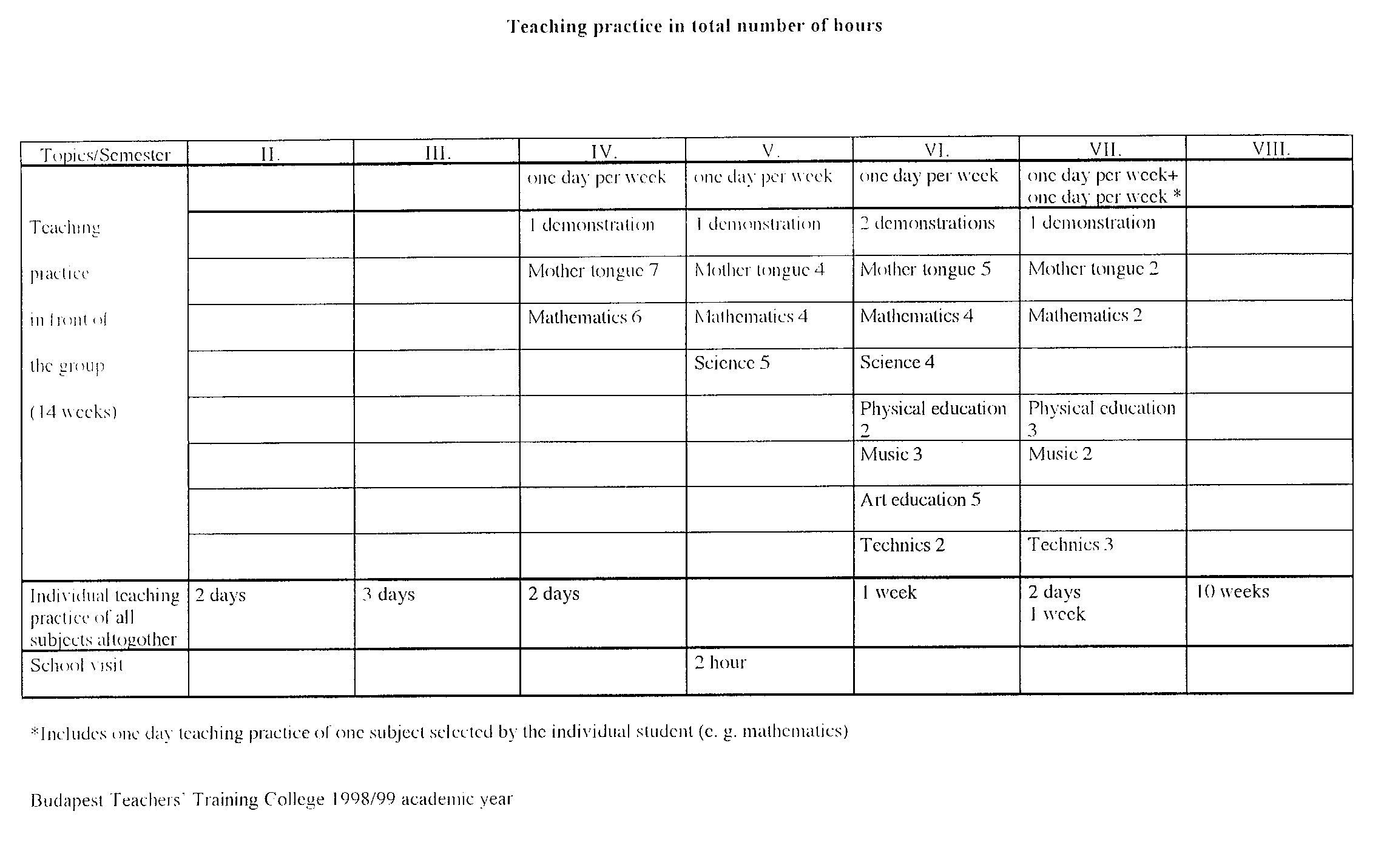
TABLE 3

Experiment and research in Hungary is not a simple task in mathematics education.

In principle this is the duty of universities and Teacher Training Colleges. In practice it has no well-established financial background of educational research. Universities have no funds for research or experiments. On the competitions of research projects didactical projects can hardly win money. The fact that mathematical education is a legal topics for PhD only since 1999 also shows that education is not a much preferred field of research in Hungary.
Actually the most part of the research and experiment work on this domain is done by volunteers.

During this work we constantly stick to our main research interest: how, and whether at all, is it possible to develop the ability of prospective mathematics and primary teachers to understand the way of thinking of their students.

In order to get closer to the main topics during the academic year 1998~99 in a class of 8-9 year old pupils we started to study the issue whether prospective teachers observing the work of the class feel identity with the pupils or with the teacher during the lessons.

Using the case of a critical period between the class teacher and a pupil observed together with the prospective teachers we tried to study the level of empathy between prospective teachers and the pupils. They had to reflect in a short paper to the lesson answering the question: 'In your opinion what was Tom thinking about during the lesson?'.

All the 13 prospective teachers put themselves into the pupil’s shoes.

2. TEACHING PRACTICE
"teaching in the presence of the group of students".

The work is carried out in the mathematics part of the practice period mentioned
under the name ‘Teaching practice in front of a group’ in the table above.

A new method was introduced gradually during the last five years at creating an environment for the student in which he/she becomes part of a group of peers and two senior educators. They work and observe together, in an interactive manner, within the classroom. With the careful, non-aggressive interpretation of the educators and continuously communicating with peers, the student comes to understand the overt and hidden processes as they happen in the class. This progress hopefully leads the student to grow, not into a "schoolmaster", but into a competent chooser or selector between alternative ways of teaching. Rather than expecting them to memorize a concrete map, they should be offered a compass and the opportunity to develop a sense of direction. Within the framework of the practice, the students is one of 16-17 members who try to explain and understand their experiences together; but in his/her future practice, he/she will be alone to predict and analyze the concrete and mental processes in the classroom.

A group of (14-15) students regularly visits the same primary class once a week with a mathematics college tutor on the same day of the week (let us say Monday).

By the planning of the process the tutor is the same person who was the leader of the mathematics seminars of the students during the previous three semesters of their studies and he/she is the teacher of the didactics of mathematics at present as well.

The whole process starts with a lesson in the class of pupils held by the class teacher who is the mentor teacher of the students.

After the lesson the teacher

presents the process of planning of this actual class activity including the apriori analysis.

makes an a posteriors analysis of the classroom activity and receives the reflections of the students

offers some additional information about the class and about the individual pupils for the prospective teachers.

Week 1. The primary teacher of the class gives the goals and tasks of a mathematics lesson which will be lead by one of the student-teachers (trainees) in one week and in two weeks. All students prepare the plan of a whole class activity at home individually.

Week 2.
a) The group of the students, the mentor teacher and the college educators together make a common plan about the activities of the maths class.They make a detailed preparatory work, an a priori analysis of the next class activity and choose two students who potentially will teach the lesson during the following week. Actually only one of them will teach, the other will be the deputy teacher who teaches only if the first is absent (e.g. becomes ill).
b) The primary teacher gives the aims, goals, objectives, tasks of the lesson in two weeks ahead for preparation.

Week 3.
a) The student teacher teaches the class. The group of students, the primary teacher and the mathematics educator take notes. The deputy student teacher gives some observation points for her/his colleagues one for each student.
b) During the same day by the leadership of the deputy student teacher the student teacher makes an a posteriori analysis of the classroom events and a self evaluation;
the group, the primary teacher and the college maths educator make reflections on the lesson.
The major aim of the common work is to be able to understand the classroom events. To use the value of what different people could see and reflect the same situations.
c) The primary teacher gives the aims, goals, objectives, tasks of the lesson two weeks ahead for preparation.

This process is repeated 6 times in the first semester and 3-3 times in the other three semesters. But the students stay together with the class and the class teacher during the semester to practice school subjects other than mathematics.

The role of the individuals taking part in the process are as follows:

1. The teacher of the pupils in the associated school who completed the syllabus for the class, and is to provide the content and goals of the given lesson. He/she reads and comments students’ plans for the lesson, checks and discusses the draft of the student who is to actually teach the class in the next period. Takes part in the mutual analysis of the experiences, and the preparation for the next lesson.

2. The educator of mathematical didactics prepares the lesson, in the presence of the teacher of the class and the members of the students’ group. When one of the students was chosen for holding the lesson, the educator discusses the student’s revised plan once more in great detail. Takes part in the mutual analysis of the experiences, and the preparation for the next lesson.

3. The educator of general didactics takes part in the mutual analysis of the experiences, and the preparation for the next lesson.

4. The main characters: the students study the curriculum of the given class and prepare for the lesson, in accordance with the contents and aims as having been specified by the teacher. They discuss and brainstorm together the drafts individually prepared for the lesson. One student is chosen for holding the lesson, and another one for being substitute in case of any prevention of the first candidate.

5. The place of the activity is the Practice School of the BTTC in the 3^rd semester and 30 different normal schools associated by the BTTC in the other semesters (teachers receive unfortunately a symbolic sum as fee).

3. REFLECTION AND EVALUATION

3.1 REFLECTION

The decisions the educators of the department made 5 years ago were the following.

1) Each educator of the department will prepare him/herself to participate in each field of the primary pre-service mathematics education namely:
a) mathematics courses,
b) didactic of mathematics courses,
c) school practice in mathematics.
2) The educator of didactic of mathematics of an academic group of students will
participate on each mathematics activities of the practical teaching activities of the same group during the four semesters of the "teaching in the presence of the group" courses
3) The main objective of our practical formation is not to create "school masters" who can navigate well on a learned map, but to try to sharpen the senses of the prospective teachers, "give compass for them".
Naturally here the human part of this decision has been expressed more simply than the organisational one. Luckily we did not change the duties of the department, because the department had to teach mathematics, didactics of mathematics and an educator had to follow the school practice together with the students.
The modification and the core of our effort is that these three roles have been carried out by the same person.

3.3 EVALUATION

Values of this kind of system are as follows:

1. The group and the educator have a common "mathematical didactic life story" during all the 8 semesters of the studies.

2. The common class experience of the students and educator give a chance for the educator to discuss theoretical questions under the frame of their common experience, the class events.

3. Ali-nost all the important theoretical issues appear in the practice when the educator immediately can indicate, explain the theoretical knowledge again but in the light of the practical work.

4. Primary teacher-mathematics educator team can cooperate well and they are legitim together in the eyes of the students. Students can practise that there are class events which the two people evaluate in different ways. There is no absolute truth in the practical situation.

5. Students start to practise a non-offensive reflection/evaluation of the work of
each other.

6. This system gives a feedback for the theoretical education. Maths educators
can focus on topics in the future with a new group of students which by the experience of the school practice activities did not seem to be well understood by their former students.

7. Primary teachers of the associated schools can be in a constant and deep working relation with the maths educators of the Teacher Training College.
 

3.4. PERSPECTIVE

Although I am aware that the framework of teacher training we use in Hungary and which I attempt to describe in my presentation is not present in the same way as in other countries, I still feel obliged to at least introduce the practice we follow as well as the leading educational principles behind them. By doing so, I, perhaps might disseminate some ideas of considering the educational benefits that a system like this can bring into lower primary education in any part of the world.
 
 

4. How is an adequate balance between knowledge of mathematical content and pedagogical abilities to teach mathematics obtained and promoted?

Our first-year students come to teachers' training college expecting to learn more math. It is only in the later years that their focus shifts to teaching it.
From our point of view it is important to integrate the teaching of additional math and the pedagogy of teaching math, because the students cannot convert their mathematical knowledge to teaching it successfully. Therefore, because of the students’ expectations, we mark the pedagogical aspects of the curriculum in the early stages. We do this by using proper mathematical terminology, but take the examples from the primary workbooks. Care must be taken to ensure that the students do not feel that their intelligence has been insulted by this.

During the first three semesters the students visit classrooms, discuss observed lessons, plan lessons and practise teaching on their own classmates. In the fourth semester they get their first opportunity to practise on school children. I will go into more detail in this topic later on in my presentations.
Their interest in the pedagogy of teaching math is suddenly awakened about the time they start to practise teach. This is very evident, because when we start to teach the pedagogy of teaching math in the third semester, it is a real struggle, but from the fourth semester on the students become much more receptive.

The most succesful periods of learning on their part occur when we can build on the student teachers’ classroom experience.

Various teachers’ colleges in Hungary differ in the way they try to promote a balance between mathematical knowledge and pedagogical abilities to teach math. Some concentrate on theory and separate the teaching of theory from didactics by having separate professors to teach the two subjects. Others teach pedagogical skills from the beginning, while our ‘mstitution aims to integrate the two areas by having the same person teach both to a given group of students.
 

5. What are the main goals and guidelines of the primary mathematics education in your country?

2.Construction:
formulation of problems, expressing hypotheses, planning the sequence of problem solving, selecting the best aids, finding one or several objects (numbers, forms, etc.) which satisfy given criteria, finding all such objects, verification, definition, generalisation, specialisation, extension by analogy.

3. Judgement:
The ability to compose true or false statements about a situation or a construction or a set of numbers.
In example: what can the student say about the winning numbers in the lottery, or a comparisson of temperatures taken in the morning vs. noontime.

Following the thought processes of another person.
For example in trying to understand different methods of solving the same problem.

The ability to recognize that the concept is the same, even though another pupil might have expressed it differently.

Simple deductions:
For example, using a question and answer format, try to fmd out where something is hidden or deduce what the hidden object is.

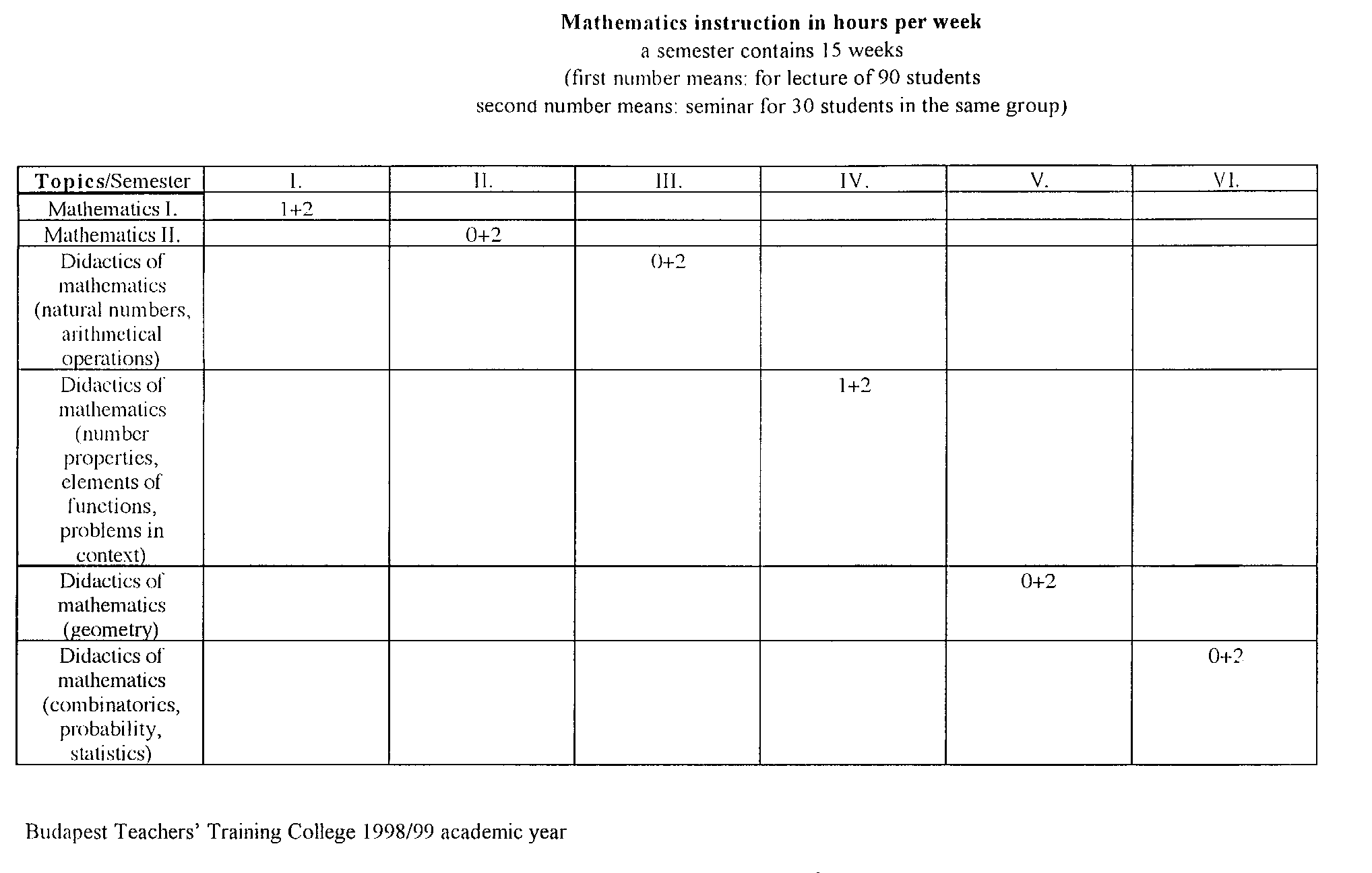
6. THE PROGRAM (TABLE 3)

1. Mathematics and Mathematics Education

six semesters, altogether 210 hours
(See in the bracket the number of lectures + number of seminars per week)

1.1 Sets and logic; relations, functions, sequences (1+2)
1.1.1 Sets
Describing sets. Set, subset, empty set, universal set. Proper subset. Complement of a set. Union, intersection, disjoint set. Properties of set operations. (Commutative, associative, identity, complement, distributive properties.) Venn diagrams as problem solving tools. Cartesian products.

One-to-one correspondence. Equivalent sets. Cardinal numbers.Ordinal numbers. Finite sets. Sets of numbers.

1.1.2 Logic
Statement. Negation. Quantifiers: universal quantifiers, existential quantifiers. Truth table. Compound statements. Conjunction, disjunction. Properties of logic operations. De Morgan’s Laws. Conditionals (implications) and biconditionals. Tautology. Valid reasoning. Direct reasoning (Law of Detachment - Modus Ponens). Indirect reasoning (Modus Tollens). Chain rule. Invalid conclusions.

1.1.3 Relations
The intuitive concept of relations. Relations as a subset of a Cartesian product. Relation on a set. Properties of relations. The reflexive property, the symmetric property, the transitive property, trichotomy. Equivalence relation, equivalence classes.

1.1.4 Functions, sequences
A function from A to B. Operations of functions. Composition of two functions. Identity functions and inverse functions. Sequences.
 

1.2 Elementary Number Theory (0+2)

1.2.1 Numbers and numeration systems
Different Numeration Systems: Egyptian, Babylonian, Mayan, Roman, Hindu-Arabic. Decimal system. Whole Numbers. Addition and subtraction of whole numbers. Number-line model. Greater-than less-than relations on the set of whole numbers. Whole-number addition properties. (Closure property of addition on whole numbers, commutative, associative, identity properties). Multiplication and division of whole numbers.

1.2.2 Elements of number theory
Divisibility. Properties of divisibility. Divisibility rules depending on the numeration system. Prime and composite numbers. Factorization, prime factorization. Factor tree.

Fundamental Theorem of Arithmetic (Unique Factorization Theorem). Sieve of Erathosthenes.There are infinitely many primes.

Greatest common divisor, least common multiple. The intersection-of-sets method, the prime factorization method. Euclidian algorithm method. Relatively prime numbers.

Modular arithmetic. Congruence, properties of congruence.
 

1.3 Mathematics Education I. (0+2)

1.3.1 General topics of mathematics education
The interpersonal nature of mathematics education. Mathematics education as a social process. Mathematical culture. Values, ideals and theories of knowledge. Investigation-based teaching. Collecting experiments, data, the exploration of possibilities, the representation of relationships, hypothetical thinking, organising experiments, the development of conjectures, conviction, argument and proof. Precision, conciseness, logical consistency, reflection on the previous topics. Social construction of meanings. Sharin and contrasting mathematical ideas. Shaping of explanations.

Development of playing as a mathematically significant activity. The role of games in developing mathematical thinking.

Curriculum, syllabus, long term and short term planning by the school and by the teacher.

The role of the teacher. Classroom organisation. Slow learners and quick learners. Learning problems in mathematics.

Evaluation, assessments and their methods.

The importance of mistakes in the learning process.

1.3.2 The teaching of the concept of natural number and operations
Preparation of the concept of natural number. Natural number as counting, used in measurement. Cardinal number, ordinal number. Addition of whole numbers, different models. Basic addition facts. Subtraction. Take-away model, missing-addent model, comparison model, number line model. Properties of subtraction. Multiplication and division of whole numbers. Repeated addition model, array model, Cartesian product model. Properties of whole-number multiplication. The distributivity property of multiplication over addition. Division of whole numbers. The partition model, repeated-subtraction model, missing-factor model. Division algorithm. Division by 0 and 1. Ordering. Properties of numbers and their relationship.

Algorithms of whole-number addition and subtraction. Algorithms of whole-number multiplication and division. Mental arithmetics. The development of the process of mental arithmetics. Computational estimations (estimation strategies).

Other number bases.

Integers and the operations of addition and subtraction. Representation of integers: thermometer model, number line model. Order of operations.

1.3.3 The use of different kind of manipulatives in mathematics education
Cousinaire rods. Dienes blocks. Dienes multi base blocks. Multi link cubes, counters. Trimat, quadrimat. Artifacts in education.
 

1.4 Mathematics Education II. (1+2)

1.4.1 Mathematical models for problem solving
Number line. Open sentences, types and their solutions. The role of open sentences as mathematical models.

1.4.2 The teaching of negative numbers and fractions.
Different models of fractions. Partition, or part of a whole. Unit fractions. Division of whole numbers and fractions. Ratio. Equivalent fractions.

1.4.3 The teaching of relations, functions,sequences
Exploration with Patterns. Development of mental and mathematical abilities by this topics.

1.4.4 The development of mental abilities by mathematics
The inductive property of mathematics learning. The possible development of the different ways of thinking: intuitive, analogous, algorithmic, logical, creative, problem-solving, combinatorial and the importance of this in the learning process.

1.4.5 Problem posing
The role of questions, the role of reflections.
Word problems. The relationship between natural languages and the language of mathematics. The role of the context. Various methods of solutions: by playing, by drawing, by mathematical models etc.
 

1.5 Teaching Geometry and Measurement (0+2)

1.5.1 Geometry
Geometrical constructions. Paper folding. Geometrical patterns.

Geometrical concepts, relationships. Angle.Triangles and quadrilaterals.

Regular polyhedra.

Networks and topological equivalence.

Congruence and similarity. Geometric constructions: constructing segments, congruent angles, parallel lines, angle bisectors, perpendicular lines, perpendicular bisectors.

Circles and spheres. Great circle, circles of latitude, circles of longitude.

Systems of location on a line in a plane in space: coordinates.

Transformation of the plane: translations, reflections, glide reflections, rotations. Properties of these transformations. Construction of transformations. Plane symmetry, rotational symmetry. Applications of symmetry in geometry. Similar triangles and similar figures. Scale-model enlargements, scaling-down.

Tessellations of the plane; regular tessellations.

Geoboards, pentominoes, colour tiles, Tangram, polyhedra blocks, solids, the Lénart sphere, construction tools.

1.5.2 Measurement:
Comparative quantifiers (faster, thinner etc.). Qualities, ordering, development of units, accuracy of units, estimation. Length, area, volume, time, temperature, weight. Conventional units, standard units, system of units.
 

1.6 Combinatorics, Probability, Statistics and its education (0+2)

Following.an inductive approach to the topics we plan to cover the concepts listed below.

1.6.1 Combinatorics
Methods of counting. Tree diagram. The Fundamental Counting Principle. Permutations of unlike objects. Permutations of like objects. Combinations.

1.6.2 Probability
Experiment, outcome, sample space, outcome set tree diagram. Impossible event, certain event. Mutually exclusive events, complementary events. Equally likely outcomes. Frequency tables. Statistical graphs: histograms and bar graphs, pictographs. Frequency polygons.

The concept of probability
determined empirically,
determined theoretically.

Geometric probability. Modelling games.

Independent events.

Simulations.

1.6.3 Statistics
The basic problem of statistics. Grouped data. Measures of central tendency and variation. Means: arithmetics mean, mode, median. Measures of dispersion. Comparing sets of data. Normal distributions. Percentiles. (Educational problems like comparing scores from different tests etc.)

Abuses of statistics.