En los capítulos que siguen veremos en primer lugar cómo el conocimiento del campo específico en que un problema se coloca puede resultar una condición absolutamente esencial para poder pensar en tener acceso a la resolución de problemas de alguna envergadura. Veremos a continuación cómo el conocimiento que nos puede prestar una ayuda más efectiva debe presentar una cierta estructuración que lo haga manejable para nuestra mente y estable en nuestra memoria. En el último capítulo de esta cuarta parte examinaremos la idea de los esquemas mentales eficaces de un campo particular, que vienen a constituir la contrapartida de las ideas inertes, y cuya detección y transmisión debería ser uno de los principales objetivos de la enseñanza.

NECESIDAD DE UN CIERTO CONOCIMIENTO DE LA SITUACIóN

Si te enfrascas un rato en el problema, es posible que te suceda lo mismo que a mí. Si descartas algunas posibles conjeturas rebuscadas, como pensar que el carretero va sentado delante y pesa muchísimo o algunas otras ideas peregrinas que te puedan pasar por la cabeza, no aciertas a pensar en razón alguna por la que el eje delantero deba sufrir más que el trasero.

Cuando decidí darme por vencido y acudir a la solución propuesta por Perelman, pude leer lo siguiente: «De todos es conocido que el diámetro de las ruedas delanteras es menor que el de las traseras ... ».

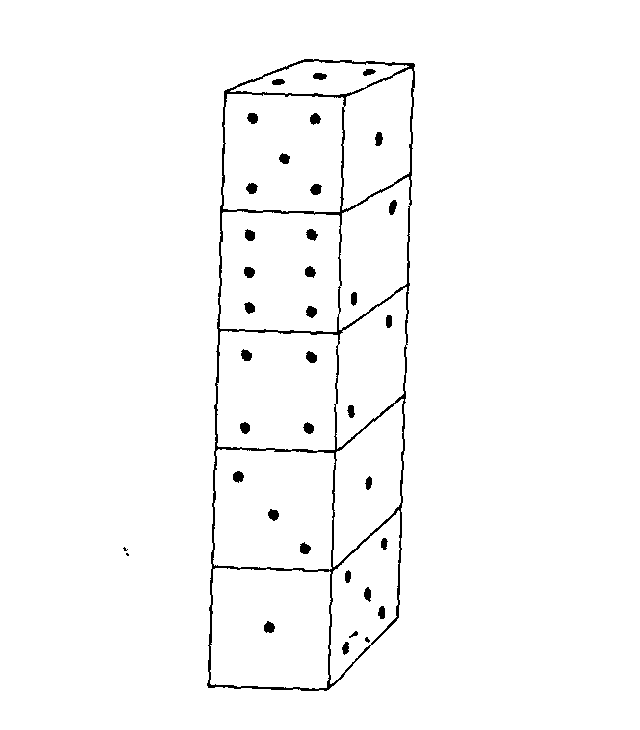
En mis experiencias como entrenador para la solución de problemas suelo comenzar a veces con el siguiente curioso ejercicio de magia.

Sin más que echar una rápida mirada, digo: «La suma de los puntos puntos de las caras que están ocultas (es decir de las horizontales que no se ven) es 32», y resulta que así es.

Resulta asombroso para casi todo el mundo. ¿Cómo puedo hacerlo? Generalmente la gente no sabe que tradicionalmente los dados se hacen de una forma muy especial. La cara del 1es paralela a la del 6, la del 2 a la del 5, la del 3 a la del 4, es decir caras opuestas suman siempre 7. Se puede especular acerca de la razón por la que se construyen así, pero el hecho es que así se hacen. Para quien lo conoce, mi truco resulta obvio. La suma de todas las caras horizontales es siempre 35. Si veo un 3 en la superior es claro que las caras ocultas suman 32.

Realmente no hay que tener un conocimiento muy sofisticado de las propiedades de un triángulo para resolver este problema. Si los lados del triángulo son a, b, c, y las alturas correspondientes son h_a, h_b, h_c, entonces sabemos que ah_{a =} bh_b= ch_c= 2S, siendo S el área del triángulo. Por lo tanto, si h_a = 1, h_b =2, h_c= 3, resulta a=2b=3c, es decir b=a/2, c=a/3. En cualquier triángulo el lado mayor es menor que la suma de los otros dos, pero aquí b+c=5a. Efectivamente Juana me está tomando el pelo.

La solución del problema no está muy alejada de lo más básico que se suele aprender acerca de un triángulo, pero está clarísimo que, a menos que tenga incorporado en mi colección de conocimientos los dos hechos importantes, S=ah_a/2 y b+c>a, me encontraré bien perdido.

El siguiente es un ejemplo un poco más complicado, también relacionado con la geometría elemental.

En uno de los trabajos de A. Schoenfeld (Problem solving in the Mathematics Curriculum, MAA Notes Nº1, The Mathematical Association of America, Washington, 1983, p. 42) aparece el siguiente problema:

1) Un lado del triángulo tiene longitud a.

2) El radio del círculo inscrito en el triángulo es r.

3) La medida del ángulo opuesto al lado de longitud a es A.

Schoenfeld relata los tortuosos caminos seguidos por los estudiantes de su clase de resolución de problemas hacia la solución.

En nuestro país, al igual que en Francía, este tipo de ejercicios constituyeron el meollo de los famosos exámenes de ingreso en las Escuelas de Ingenieros hasta los años sesenta, para cuya preparación los estudiantes habían de hacer decenas de tales ejercicios diariamente. Para casi cualquiera de los individuos sometidos a la baqueta del FGM o del Rouché-Comberousse, los tratados que constituían la base de tal preparación, este ejercicio hubiera sido inmediatamente resuelto como sigue.

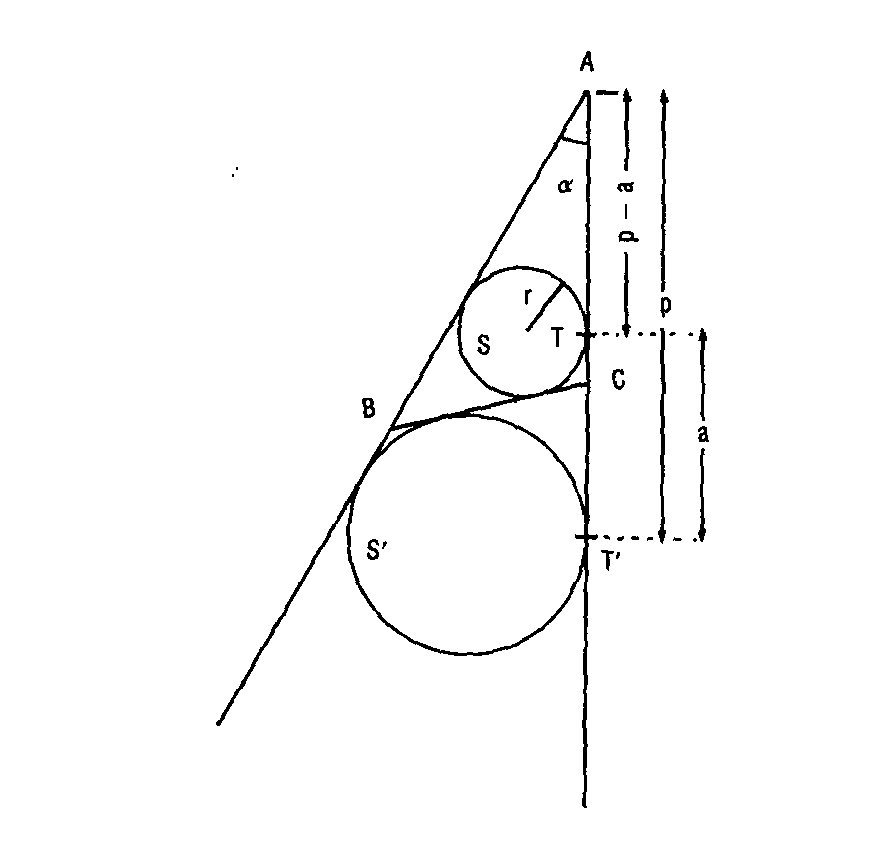
Trazo un ángulo de amplitud A a cuyo vértice le llamo asimismo A. Trazo el círculo S de radio r inscrito en este ángulo.

Supongo que el triángulo pedido, por ahora desconocido, sea el ABC de la figura. Trazo el círculo exinscrito señalado. Yo sé que AT=p-a y que AT'=p. Así, TT'=a. Como con los datos del problema conozco T, puedo obtener T' sin dificultad. Con r puedo trazar fácilmente el círculo S', exinscrito. Para obtener el triángulo ABC sólo tengo que trazar la tangente común a S y S'. Dos soluciones que dan dos triángulos simétricos.

Otra solución hubiera podido ser la obtenida por los estudiantes de Schoenfeld,

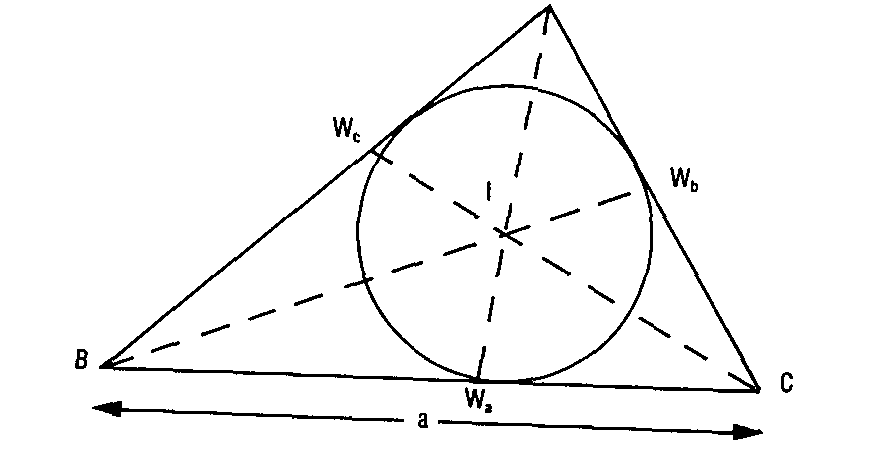
Supongamos el problema resuelto. Trazamos las tres bisectrices que se cortan en el centro del círculo inscrito. Ahora con un poco de astucia nos enteramos de que, puesto que un ángulo exterior en un triángulo es la suma de los dos interiores no adyacentes a él,

Así, BIC = A + (B+C)/2 = 90º +A/2

Por tanto I está en el arco capaz desde el que se ve BC=a bajo un ángulo de 90º+A/2. Lo trazo. Por otra parte, I está a una distancia r de BC, es decir sobre la paralela a BC a distancia r del mismo lado que ese arco capaz. La trazo. Cada intersección de las dos líneas da una posición posible de I. Trazo la circunferencia inscrita y luego las tangentes desde B y C para obtener A. Dos soluciones simétricas.

Los ejemplos propuestos ilustran convenientemente el papel fundamental que puede jugar el conocimiento de la materia a la que se refiere un problema.

Si no sabemos cómo es la carreta a la que se refiere Perelman, mal podemos dar con la solución a su problema. Si no sabemos que los dados se hacen normalmente como he explicado, el truco de los dados puede parecer verdadera magia. Si nuestro conocimiento de la geometría del triángulo es escaso, el problema de Juana y mucho más el de Schoenfeld nos puede ocupar un rato bien largo y nuestra solución resultará posiblemente fea y farragosa.

Resolver un problema consiste en enlazar los datos entre sí y con nuestros posibles conocimientos y hallazgos previos de tal forma que se origine un contexto nuevo, una reestructuración de nuestros conocimientos que nos permita realizar la tarea prefijada.

Un problema se presenta siempre dentro de un cierto contexto y, a menos que poseamos ya o podamos adquirir un conocimiento más amplio de tal contexto, nuestras posibilidades de resolución serán ciertamente escasas. Aun en el caso de que poseamos una buena dosis de sabiduría y experiencia en lo que se refiere al uso de estrategias heurísticas, éstas no pueden trabajar en el vacío. La bordadora más habilidosa no llegará a ningún resultado sin colocar hilo en su aguja.

Si los puzzles, los acertijos y las recreaciones mentales elementales, como la mayor parte de las que se han presentado en la tercera parte, pueden resultar verdaderamente estimulantes, retadoras y formativas para un público amplio es precisamente porque tanto el contexto en que se coloca el enunciado como el conjunto de conocimientos necesarios para resolverlas está, sin preparación previa, a disposición de todos. Lo único que se necesita es emplear correctamente la capacidad de visión y exploración presente en todos nosotros, que es de lo que aquí se trata fundamentalmente.

Pero a medida que va uno adentrándose en problemas pertenecientes a un campo más específico, la conveniencia o la necesidad de una información más profunda se hace patente. He aquí un par de casos significativos.

No quisiera que estos ejemplos fuesen mal interpretados. No pretendo en absoluto defender que estos conocimientos deban formar parte de los contenidos de nuestra enseñanza a ningún nivel, ni primario, ni secundario, ni terciario. El debate sobre cuál debería ser el contenido de nuestros programas de enseñanza de la geometría está muy lejos de terminar. Mi objetivo al presentar estos ejemplos es sencillamente tratar de dejar bien claro que un mero dominio de estrategias mentales es totalmente insuficiente para resolver un problema de cierta envergadura en un campo específico. Un modo correcto de utilizar la capacidad mental es lo mejor que nuestro sistema de enseñanza puede proporcionar a nuestros estudíantes, pero no pensemos que con sólo esto ya están plenamente capacitados para grandes proezas intelectuales.

El tipo de conocimiento verdaderamente útil en la resolución de problemas se compone de

Hechos y circunstancias importantes relacionados con los elementos del problema.

Familiarización con las técnicas específicas del campo en que se encuadra el problema mismo.

Los hechos y circunstancias de interés no deben constituir un amasijo mental de datos meramente yuxtapuestos, sino que se debe tratar de un conocimiento bien estructurado y dinámico, de tal forma que, una vez propuesto el problema, surjan en nuestra mente, como de modo reflejo y automático, constelaciones de hechos en las que se puedan encajar los datos y la situación del problema de manera que así resulte la solución ocupando entre ellos su lugar natural, como en los ejemplos que hemos visto. Este punto será tratado con más detalle en la sección siguiente.

Las técnicas específicas del campo son estrategias particulares, modos de proceder inteligentemente en él que han sido consagradas por la tradición y el ejemplo de los grandes expertos en la materia correspondiente. Como hemos visto en la tercera parte, al considerar en particular el campo de las ideas matemáticas, aparte de las estrategias que son comunes a otros muchos posibles continentes mentales, surgen estrategias que, aunque de largo alcance y utilizables y utilizadas en todos los rincones de la matemática, como la inducción, son muy específicas del pensamiento matemático.

Pero incluso cuando uno estrecha el enfoque sobre campos más concretos, Como puede ser, por ejemplo, el estudio de las sucesiones y series numéricas, surgen estrategias aún más específicas que podríamos describir como las técnicas modélicas propias del campo, los paradigmas específicos de la materia en cuestión, que vienen a explicitar modos útiles de proceder y aceptados por la comunidad de expertos en el campo, avalados tal vez por la experiencia de siglos.

La distinción entre los hechos y situaciones importantes por un lado y las técnicas propias del campo por otro no es muy nítida, ni tampoco importa mucho que lo sea. Lo que importa es la realidad, no el nombre.

Que un número entero cualquiera admita una única descomposición en factores primos es un hecho central de la teoría de números y al mismo tiempo una de las técnicas más fructíferas en la resolución de problemas en este campo.

Una exposición razonable de un campo cualquiera, como la que debería estar en la base del aprendizaje a cualquier nivel, debería preocuparse fundamentalmente por entresacar del acervo acumulado alrededor de tal área aquellos hechos, situaciones, técnicas, que sirven de modelo para mostrar la eficacia en la resolución ción de los problemas típicos que aparecen en dicho campo.

Si en matemáticas se propone un teorema, si en física se subraya un principio, es necesario que se vea al tiempo cuál es su eficacia, de qué situaciones proviene, qué explica y qué tareas viene a resolver. De otro modo el aprendizaje se convierte en huera erudición y en una mera acumulación de ideas inertes.

Podríamos recapitular las consideraciones anteriores de la forma siguiente:

El conocimiento de los contenidos en que se encuadra un problema es extraordinariamente importante para su resolución. No se puede pensar que el conocimiento de estrategias generales del pensamiento, por sofisticado que sea, puede suplir al conocimiento puntual del campo concreto. El estudio de un área específica de las matemáticas, por ejemplo, no se puede sustituir por el estudio de las estrategias de pensamiento generales más una somera información de los principales conceptos y principios tal materia concreta, pensando que, con estos elementos, el que se inicia será capaz de adentrarse por sí mismo y resolver los problemas típicos del campo. Es necesario los modelos del pensamiento específico de tal área concreta.