De no ser por la presencia del infinito, la matemática no pasaría de ser una inmensa y superficial tautología. Pero el infinito está presente en el pensamiento matemático, constituyendo la misma raíz de su posibilidad. En la conciencia misma de la unidad propia, la mente percibe su pensamiento en el horizonte del infinito como repetible, como no llenándolo todo... Del uno al dos y está ya el infinito presente en el proceso.

De la confrontación con el infinito, de los sucesivos ensayos mentales para lograr el dominio de los procesos infinitos, han surgido las grandes creaciones de las diferentes etapas de la evolución matemática. Primero en forma confusa caótica produciendo convulsiones mentales, a veces fuertemente traumáticas, como en el caso del descubrimiento del número irracional entre los pitagóricos. Más adelante, al ir desvelando el orden dentro del caos inicial, el pensamiento matemático se percata de que la visión inicial ingenua no ha sido destruida, sino inmensamente enriquecida, y de que el caos anterior se le ha convertido en un nuevo cosmos esplendente.

Este ha sido el itinerario mental del matemático en los puntos de cambio de rumbo de la evolución de su pensamiento.

La ocupación intensa con los fractales en la matemática contemporánea puede muy bien ser explicada dentro de esta misma dinámica del pensamiento. A comienzos de nuestro sigIo surgió de modo natural, especialmente en conexión con el estudio del análisis armónico, la necesidad de explorar la estructura geométrica de conjuntos de puntos de la recta que, aunque pequeños e insignificantes en ciertos respectos (medida de Lebesgue nula), poseían propiedades geométricas, aritméticas, analíticas, que los convertían en micromundos muy peculiares. Como ha sucedido a lo largo de la historia de la matemática muchas veces, estos entes fueron considerados en un principio como horrores, caprichos, juguetes sin mayor importancia. A medida que se fueron encontrando procedimientos eficaces para distinguirlos, medirlos, estudiarlos desde diferentes puntos de vista, los matemáticos fueron comenzando a percibir, primero la belleza interna, la armonía, la diversidad de tales creaciones, y luego, al conocerlos más de cerca, se fueron percatando de sus semejanzas con procesos y formas de la naturaleza misma y de otros objetos de diferentes campos de la ciencia, sus aplicaciones.

En el estudio de los fractales tiene capital importancia un refinamiento de la medida de Lebesgue, que es la forma natural de medir los conjuntos a través de la idea de longitud ordinaria. Se trata de la medida de Hausdorff, que permite diferenciar drásticamente entre los conjuntos pequeños, de medida de Lebesgue nula. Una breve idea no técnica de lo que viene a hacer la medida de Hausdorff se puede obtener del siguiente modo. Si el intervalo [0,1] de la recta de los númeos reales se reparte en intervalos de diámetros muy pequeños se eleva a la potencia s (un número entre 0 y 1) cada uno de estos diámetros y se suman los números resultantes, entonces esta suma se puede hacer tan grande como se quiera escogiendo adecuadamente los intervalos pequeños. Pero existen conjuntos de puntos del intervalo (0,1) tales que al realizar esta misma operación (recubrir el conjunto con intervalos muy pequeños ... ) se obtiene siempre un número finito que no se puede hacer arbitrariamente grande ni arbitrariamente pequeño mediante la elección de los intervalos, Tal conjunto tiene dimensiones de Hausdorff s. Los fractales de la recta son sus conjuntos de puntos con dimensión de Hausdorff s entre 0 y 1. Algo análogo se puede considerar en el plano
y en el espacio.

Hacia los años veinte, A. S. Besicovitch comenzó a interesarse con éxito por las propiedades geométricas (existencia de «tangente», cómo se proyectan en diferentes direcciones, densidad ... ) de los conjuntos planos de puntos con dimensión de Hausdorff 1. Sus técnicas, de gran ingenio, fueron revelando una teoría matemática de una impresionante riqueza, Se creó así la teoría geométrica de la medida, que fue más adelante explorada y extendida en el estudio de otros fractales más generales, y que es aún una rama joven de la matemática, en plena evolución y con multitud de problemas abiertos y de conexiones profundas con otros campos todavía por explorar a fondo.

Multitud de fractales interesantes, comenzando con el conjunto de Cantor clásico,
de dimensión de Hausdorff log2/1og3, se construyen mediante un proceso infinito de iteración de una misma operación bien especificada, que suele dar lugar a conjuntos autosemejantes, es decir, conjuntos tales que cualquiera de sus partes más pequeñas viene a reproducir el conjunto total sólo que a otra escala diferente. He aquí uno de los lazos de conexión entre temas tales corno la teoría de iteración, sistemas dinámicos y ciertos temas de la física, como la renormalización en el estudio de las transiciones de fase magnética,

El sistema dinámico que constituye el eje fundamental de la obra que comentamos es un proceso matemático de gran simplicidad, y en ello radica precisamente una de las fuentes de la belleza profunda que la obra encierra. Fijemos un número complejo c. Partiendo de un punto cualquiera del plano complejo, z_o, vamos a ir obteniendo sucesivamente

La figura, realizada por ordenador, muestra el conjunto de Mandelbrot. En él se 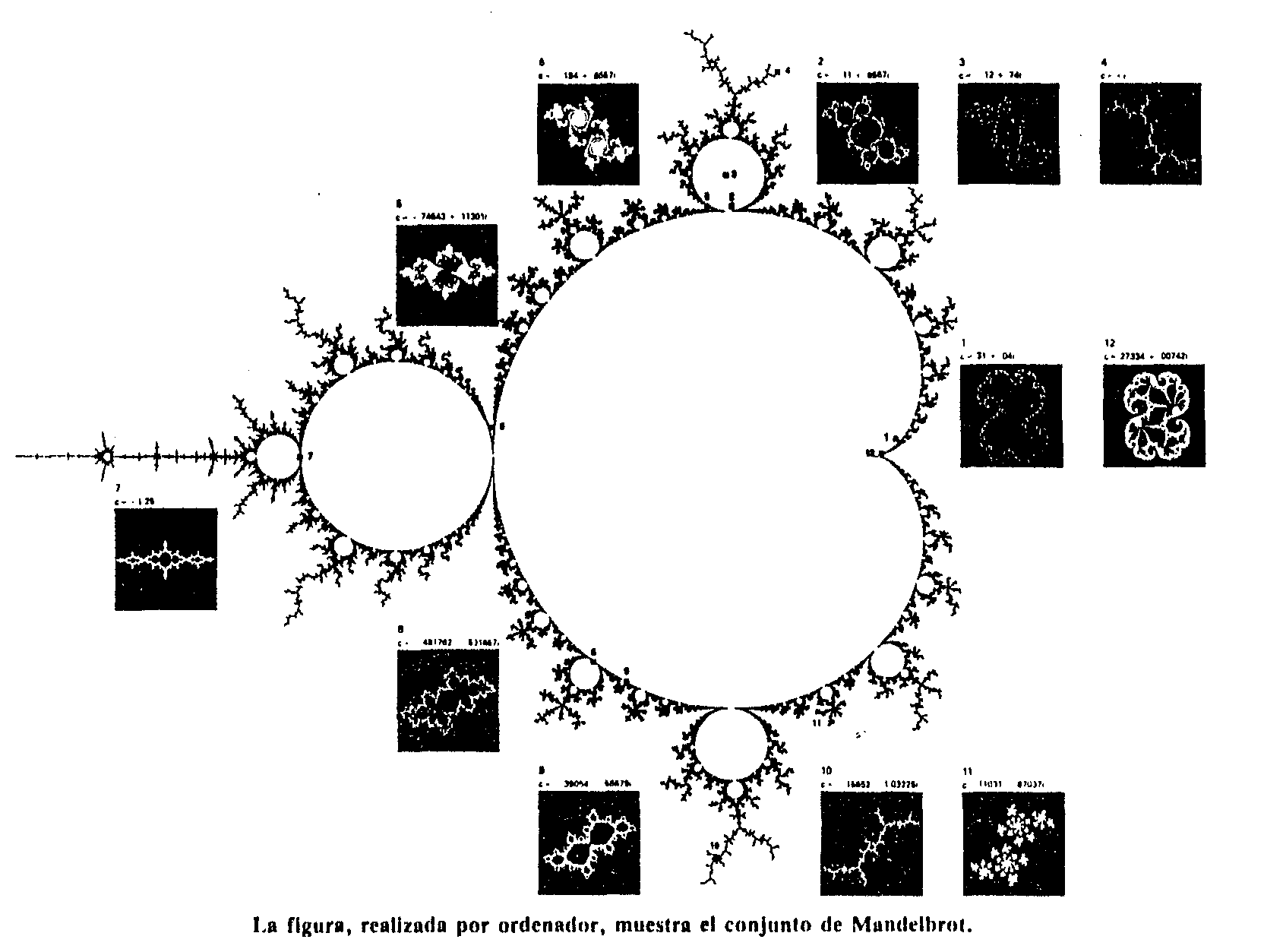han escogido doce puntos c, cuyo valor se señala en los recuadros correspondientes. Cada uno de ellos contiene una imagen del conjunto de Julia correspondiente. Llama la atención la variedad extraordinaria de formas a las que un proceso aparentemente tan sencillo como el señalado puede dar lugar.

Pudiera parecer que las consideraciones que dan lugar al conjunto de Mandelbrot y a los conjuntos de Julia son productos del ocio del matemático. Nada más falso. Muchos son los procesos naturales que admiten una modelización matemática que conduce a sistemas dinámicos no lineales semejantes al anterior. Entre ellos, por ejemplo, el proceso de crecimeinto de una población en el que se tienen en cuenta los límites impuestos por el entorno, proceso de Verhulst.

No es casualidad que las teorías que confluyen alrededor de los fractales hayan experimantado un fuerte impulso con los avances actuales de la informática. Los fractales autosemejantes, la teoría de la iteración, los sistemas dinámicos, basan sus consideraciones en la repetición, en principio infinita, de un cierto proceso bien determinado. El ordenador actual, con su versatilidad gráfica cada vez más perfeccionada, poder de resolución, ampliación, colores, etc., permite seguir este proceso iterativo hasta puntos del todo insospechados hace unas decenas de años, aunando así nuestros esfuerzos intelectuales con las posibilidades crecientes de nuestra intuición espacial y de nuestra sensibilidad estética. El ordenador se convierte así en un potente auxiliar que no sólo contrasta teorías, hipótesis y conjeturas, sino que proporciona también pistas muy valiosas que iluminan poderosamente el camino por recorrer.

La obra que comentamos está concebida como una obra de arte, nacida originariamente como una exposición de láminas en color, producidas mediante ordenador, con la finalidad de poner de manifiesto aspectos profundos de la estructura compleja de los conjuntos que surgen de modo natural en el estudio de ciertos sistemas dinámicos. El gran interés con que este trabajo fue acogido tanto por científicos como por artistas y público en general animó a los autores a producir inicialmente un folleto explicativo titulado «Harmonie in Chaos und Kosmos» y a montar más tarde varias exposiciones y publicaciones en las que aparecían reflejadas sus excursiones por el mundo de los fractales. La editorial Springer se animó finalmente a publicar las láminas y los ensayos que componen el libro con un esmero que hacen de él una verdadera obra de arte En él se pone bien de manifiesto mediante imágenes y fórmulas, lo que los matemáticos de todos los tiempos han sentido en profundidad: que la creación matemática comporta un sinfín de rasgos en común con la actividad del artista y que, como ya lo entendieron los pitagóricos del siglo VI a. de C., es fuente de elementos de belleza muy peculiar.

La obra está construida alrededor de un núcleo de unas 100 láminas a todo color de una belleza extraña y fascinante, que manifiesta en unos casos el orden abigarrado y barroco, como camino del caos, de los conjuntos de Julia y de ciertas porciones del conjunto de Mandelbrot antes descrito. En otros casos se manifiesta un tipo de belleza de sabor más moderno, que corresponde a ciertos conjuntos que surgen de otros sistemas dinámicos en el plano euclídeo real.

Dos ensayos de exposición no técnica de los autores proporcionan, incluso a los no expertos, una visión suficiente para intuir en qué consiste el quehacer con los fractales, mientras que otras diez secciones más técnicas contienen una buena guía para adentrarse en aspectos más profundos del tema. Al final se presentan cuatro ensayos elaborados para esta obra por autores que han reflexionado profundamente sobre el campo. B. B. Mandelbrot presenta las motivaciones y la evolución de su pensamiento, que fue el catalizador, en los tiempos recientes, del fuerte relanzamiento de los fractales en diferentes áreas. A. Douady presenta una descripción muy legible e interesante de los conjuntos de Julia y Mandelbrot. G. Eilenberger y H.W. Franke, en sendas contribuciones, analizan diversas implicaciones filosóficas y artísticas del tema.