TEORÍA:

1. Vectores

2. Trigonometría

VECTORES

Existen dos definiciones diferentes sobre vectores, la primera hace referencia a puntos en un sistema de coordenadas y la segunda a objetos con magnitud y dirección. Según el problema en el que nos encontremos es mejor emplearlos de una u otra manera.

Por ejemplo podemos considerar la traslación de tres unidades a la derecha y una hacia arriba que se traduce en la suma del vector (3,1), de este modo el punto (7,8) pasaría a ser el (10,9) y una traslación de este tipo sobre un plano entero pasaría a trasladar todos y cada uno de los puntos de dicho plano.

Normalmente se escoge un solo elemento del conjunto infinito, mediante el cual hemos definido los vectores, como representante de dicho conjunto. Por ejemplo, si vamos de O a A y denotamos este desplazamiento como OA esto es diferente de tomar la misma distancia con otra dirección y es diferente, también, de tomar la misma dirección con distinta distancia. Si O es un punto particular, el vector OA es un segmento dirigido particular del conjunto infinito definido anteriormente.

Si continuamos desplazándonos del punto A al punto C mediante el vector AC el desplazamiento total de O a C es la suma de estos dos vectores (OA+AC= OC). Esto queda representado por la Ley del Triángulo en el siguiente cuadro que es utilizado para la suma vectores:

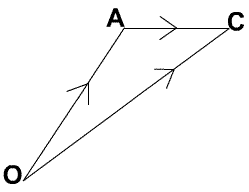
Un ejemplo práctico en el uso de vectores sería el de la navegación, donde la velocidad real de un avión vendría dada por la combinación de velocidades del viento junto con la velocidad del avión, si estuviese el aire en calma. En nuestro triangulo si tomásemos OC como la dirección necesaria para llegar al destino y AC representa la velocidad del viento entonces el piloto ha de tomar el rumbo en dirección OA con una velocidad calculada de modo que los lados del triangulo representen las velocidades.

Hemos visto el caso en dos dimensiones. ¿Qué sucede en tres dimensiones?

 Un sistema tridimensional de coordenadas es simplemente un conjunto infinito de ternas ordenadas de números reales (x,y,z) y cada punto viene dado por uno de esos triples ordenados, llamados coordenadas del punto. A cada vector libre (o traslación) le corresponde un vector de posición que es la imagen de origen sobre dicha traslación. Por tanto definimos un vector de posición como puntos en el espacio y para cada vector de posición P hay un segmento dirigido OP que determina un conjunto de segmentos paralelos dirigidos dando un único vector libre.

 Si el punto A tiene coordenadas (xa,ya,za), entonces tiene un vector de posición a= (xa,ya,za).

 Con frecuencia es útil para trabajar sólo con vectores de posición y no con vectores libres. Si bien existe una distinción conceptual entre los vectores libres y vectores de posición se puede utilizar indistintamente ambos tipos, pero esto puede causar confusión si no tenemos claras las definiciones.

La magnitud del vector de posición a = (xa,ya,za) se define como
 a=(x2a+y2a+z2a)12

y esta es la longitud del segmento OA y por lo tanto también la magnitud del vector libre correspondiente.

Los vectores i=(1 0 0), j=(0 1 0) y k=(0 0 1) son vectores de la unidad de longitud paralela a las x, y, z. El vector de posición o punto A y el vector libre correspondiente que consiste en todos los segmentos paralelos a OA también puede ser escrito como xai+yaj+zaj.

Suma y resta de vectores

Para sumar vectores de posición sumamos sus componentes. Por ejemplo, si a=(ax,ay,az) y B=(bx,by,bz) son vectores de posición, entonces a+b=(xa+xb,ya+yb,za+zb). La Ley del Paralelogramo se utiliza para sumar vectores de posición quedando OA+OB=OC.

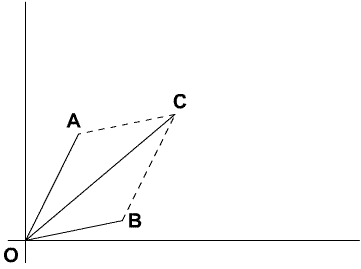
Como vector libre OB=CA la Ley del Paralelogramo de vectores de posición es análoga a la Ley del Triángulo de los vectores libres.

Cada punto A en el espacio es un vector con iguales componentes que las coordenadas del punto, por ejemplo a=(xa,ya,za). La imagen del punto A en el origen es el punto A' con el vector de posición a'=(-xa,-ya,-za). El resultado de sumar estos dos vectores te da el vector cero. Para restar el vector a partir del vector c sólo hay que sumar los vectores c y -a.

Multiplicación de un vector por un escalar

Ya hemos visto la multiplicación escalar cuando escribimos (xa,ya,za)=xai+yaj+zak. Aquí los vectores i, j y k se multiplican por los escalares xa, ya y za.

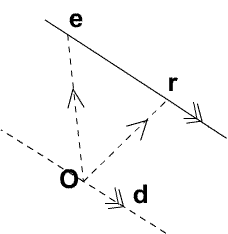
Uno de los usos de la multiplicación de vectores por escalares es la de escribir la ecuación de una recta utilizando vectores. Si d es un vector a lo largo de una recta entonces cualquier otro vector a lo largo de la recta es un múltiplo de d y llamarmos a d vector dirección de la recta. Al escribir la ecuación de una recta se utiliza la notación r = (x,y,z) para el vector de un punto general en la recta, e = (x1 y1 z1) para el vector de un punto particular perteneciente a la recta, s como un escalar arbitrario y d = (l,m,n) para un vector dirección a lo largo de la recta. La ecuación vectorial de la recta es entonces r = e + sd.

Como hemos visto hay dos tipos distintos de vectores, pero está permitido pasar de una a otra cuando sea conveniente hacerlo.

 

TRIGONOMETRÍA

Algunos aspectos básicos utilizados en la resolución del problema los recordaremos en esta pequeña introducción a la trigonometría:

Sea un triángulo rectángulo veamos algunas relaciones trigonométricas:

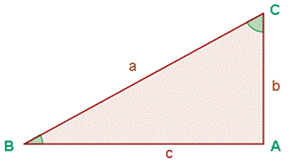
·         SENO del ángulo B: es la razón entre el cateto opuesto al ángulo y la hipotenusa. Se denota por sen B.

·         COSENO del ángulo B: es la razón entre el cateto contiguo al ángulo y la hipotenusa. Se denota por cos B.

 ·         TANGENTE del ángulo B: es la razón entre el cateto opuesto al ángulo y el cateto contiguo al ángulo. Se denota por tg B.

En el ejercicio también haremos uso de 2 proyecciones. Debido a la dificultad de explicar las proyecciones se utilizarán las fórmulas directamente para hallar los diversos datos. Nuestras proyecciones consisten básicamente en dado un dibujo en 3 dimensiones proyectar frontalmente ( como si estuviéramos viendo una de las paredes de nuestra casa) y proyectar hacia arriba ( como si viéramos el techo):

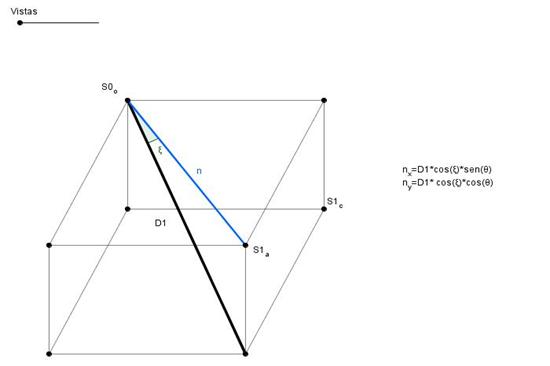
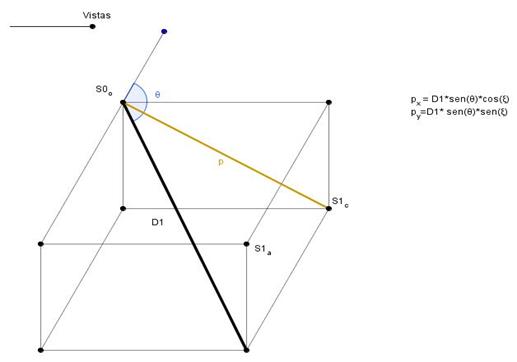
Este proceso se recoge en el siguiente ejemplo simple de las proyecciones en GeoGebra.