RESOLUCIÓN DEL PROBLEMA DEL GRAFO NO DIRIGIDO:

PASO 0:

Lo más importante es plantear el grafo correctamente.

Lo que hemos hecho ha sido utilizar Geogebra para pintar el grafo: los vértices son puntos que seleccionamos desde donde queramos pero cumpliendo las restricciones que marcan las distancias de las calles para que la escala esté acorde con el mapa; y las aristas son segmentos que unen dichos puntos.

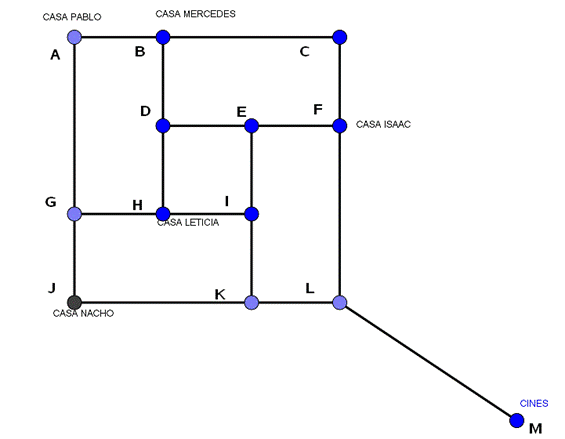
Este es el grafo asociado al problema y a partir de aquí empezaremos a resolverlo para obtener la ruta más corta que debe recorrer la cabalgata.

Es importante hacer notar que el vértice fuente (de donde sale Pablo) es el primer vértice, el de la casa de Pablo.

Lo que debemos hacer ahora es asignar a cada arista su longitud (o peso en términos de teoría de grafos), teniendo en cuenta las distancias que nos da el mapa y también cómo son las manzanas y las calles.

PASO 1:

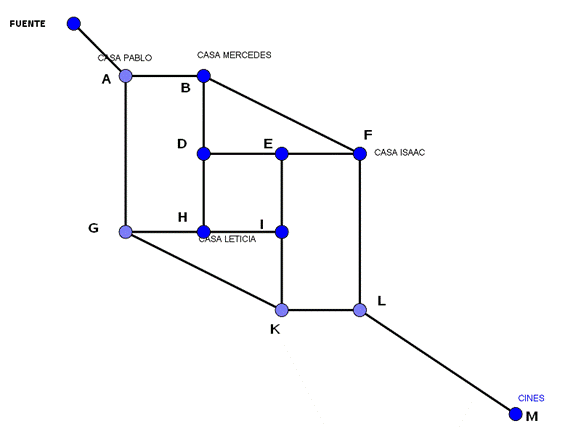
Llamamos X al conjunto de vértices del grafo que tengan grado impar:

X={B,D,E,F,G,H,I,K,L,M}

PASO 2:

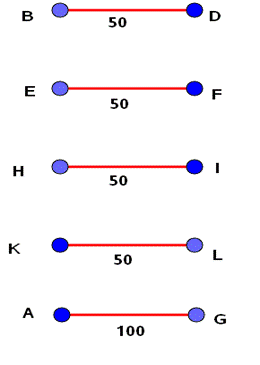
Ahora tenemos que encontrar un emparejamiento perfecto de mínimo peso (o mínima longitud).

Esto es, buscar aristas de mínimo peso que no sean consecutivas.

En nuestro problema nos queda:

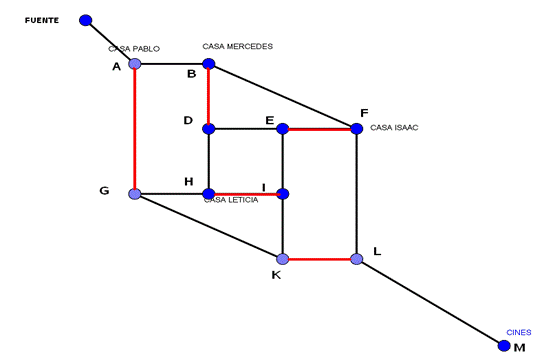
Esto es:

Ponemos ahora las aristas de los emparejamientos de manera doble en el grafo inicial, para así poder observar la solución óptima.

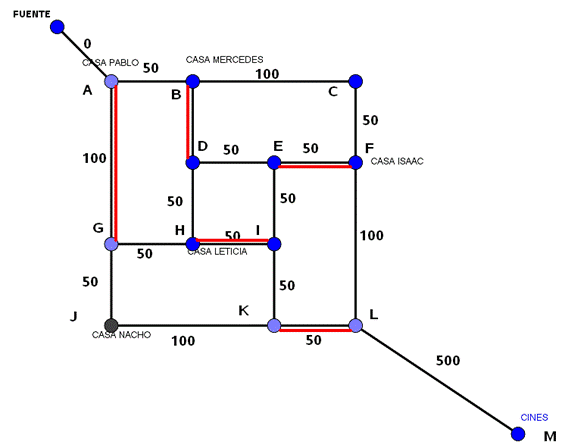
 PASO 3:

Con estos emparejamientos ya podemos encontrar a simple vista el camino de mínimo peso o mínima longitud, que es:

A – B – C – F – E – D – B – D – H – G – A – G – J – K – I – H – I – E – F – L – K – L – M.

Con  una longitud o peso de: 1800 metros que son 1,8 km.