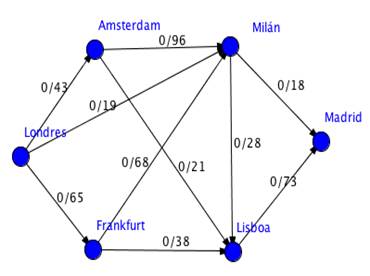

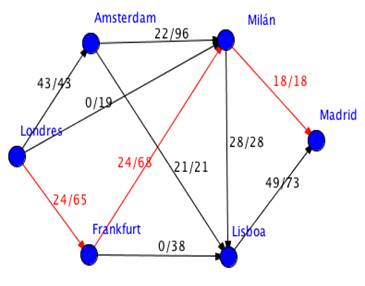
La forma más sencilla de abordar el problema es modelizándolo a través de un grafo. A continuación se muestra el grafo donde cada arista es un vuelo, y tiene asociado el número de plazas disponibles y la cantidad de ellas que vamos a asignar a nuestros clientes cuyo vuelo ha sido cancelado. Trabajaremos sobre este grafo para obtener la solución óptima.
Este problema se puede enmarcar en los problemas de flujo máximo, pues reúne las siguientes condiciones:
Es modelizable como un digrafo cuyas aristas están valoradas con valores enteros y positivos.
Existe un vértice de partida y otro de llegada (en teoría de grafos se conocen como “fuente” y “sumidero”).
El objetivo es enviar la mayor cantidad de unidades (pasajeros en nuestro caso) desde Londres (vértice fuente) hasta Madrid (sumidero).
Para resolver un problema de flujo máximo existen varios algoritmos, como el de Edmonds-Kars o el de Ford-Fulkerson. En este caso usaremos éste último. Este algoritmo lo que hace, a cada paso, es encontrar un camino que permita enviar unas cuantas unidades desde la fuente hasta el sumidero. Una vez concretado este camino se calcula la red residual, esto es, el grafo que queda cuando se ocupa el camino en cuestión con la cantidad de unidades concreta. Veámoslo con más detalle en el primer paso de nuestro ejercicio.
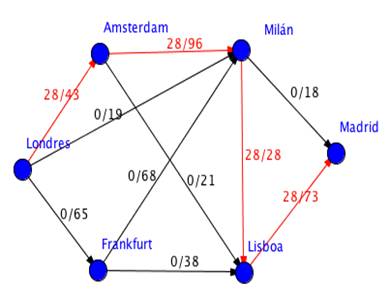
En este primer paso salimos de Londres y escogemos el primer vértice que encontramos, Amsterdam en este caso. Repetimos desde cada vértice hasta crear un camino que una Londres y Madrid. En nuestro primer paso el recorrido es Londres – Amsterdam – Milán – Lisboa – Madrid. Tomamos el menor valor de las aristas que forman el recorrido, que será la cantidad máxima de pasajeros que pueden hacer dicha ruta, 28 en nuestro caso, y lo apuntamos en cada una de las aristas que forman parte de la ruta.
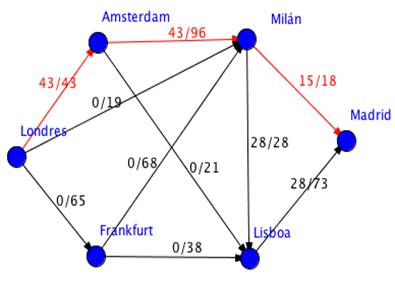
Ahora repetimos el proceso, pero teniendo en cuenta los pasajeros que ya hemos enviado a través de nuestra ruta anterior, y de esta manera vamos saturando las aristas (llenando las plazas vacantes de nuestros vuelos). En esta segunda ruta (Londres – Amsterdam – Milán – Madrid) la cantidad máxima de pasajeros es 15, pues ya habíamos usado 28 de las 43 plazas disponibles en el vuelo Londres – Amsterdam.
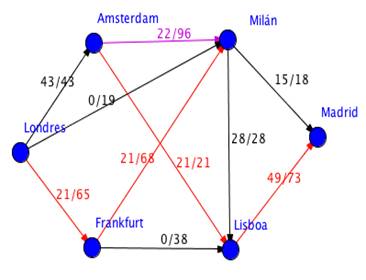
Siempre que una arista esta siendo usada podemos recorrerla en sentido contrario. En nuestro caso estamos usando en sentido contrario el vuelo Amsterdam – Milán. Veamos que está sucediendo realmente. De los 43 pasajeros que habíamos asignado al vuelo Amsterdam – Milán mandamos a 21 a Lisboa, pero siguen llegando 43 a Milán, pues estos 21 que no llegan desde Amsterdam llegan ahora desde Frankfurt.
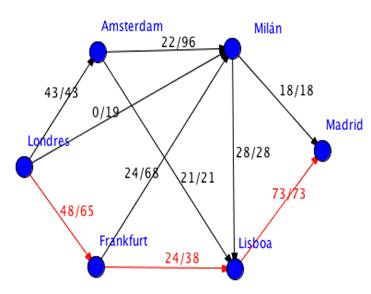
Repitiendo el proceso (solo dos veces más en este caso), finalmente obtenemos una forma de enviar la mayor cantidad de pasajeros desde nuestro origen (Londres) hasta el destino (Madrid). Observamos que habrá un pasajero que no podrá conseguirlo, pues dadas las condiciones solo podemos enviar 99.
Para visualizar este algoritmo podemos usar el siguiente applet:
http://www.cs.pitt.edu/~kirk/cs1501/animations/Network.html