INTRODUCCIÓN HISTÓRICA DE TEORÍA DE GRAFOS:

        Durante el primer tercio del siglo XVIII, en la ciudad de Königsberg (hoy Kaliningrado) se planteó un famoso problema conocido como el problema de los siete puentes de Königsberg.

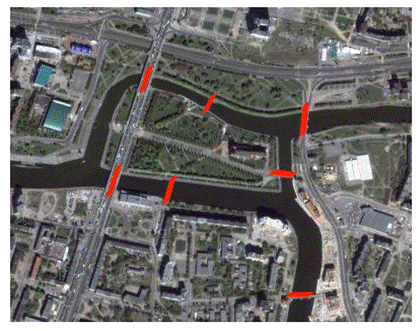
         En esta ciudad y en aquel momento, existían siete puentes que cruzaban el río Pregel (actualmente solo hay cinco), conectando las cuatro regiones que separaba este. A la izquierda una imagen actual, donde se encuentran señalados en rojo los puentes que hubo.

         Por aquel entonces los ciudadanos se planteaban si existía alguna ruta que permitiese cruzar todos los puentes una y solo una vez.

         La solución a este problema llegó en 1736 de mano de Leonard Euler (Basilea 1707, San Petesburgo 1783), cuando éste demostró que no era posible.

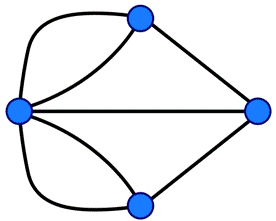
         Para su demostración lo que hizo fue modelizar la situación para quedarse solo con aquello que era trascendente para el problema, en este caso las cuatro regiones y los siete puentes que las conectaban.

         La estrategia de resolución del problema se considera la primera piedra de la Teoría de Grafos, así como de la topología. Sencillamente observó que para que en un grafo de este tipo se pudiese recorrer cada arista una y solo una vez, era necesario que a cada vértice llegara un número par de aristas, salvo a lo sumo dos vértices (inicial y final), y en este caso todos los vértices tienen un grado impar.