SOLUCIONES MODELO DE 2 OBJETOS

 Ejercicio 1

Construye un modelo en el cual la relación de velocidades entre ambos seres sea v₁=2v₂.

Solución:

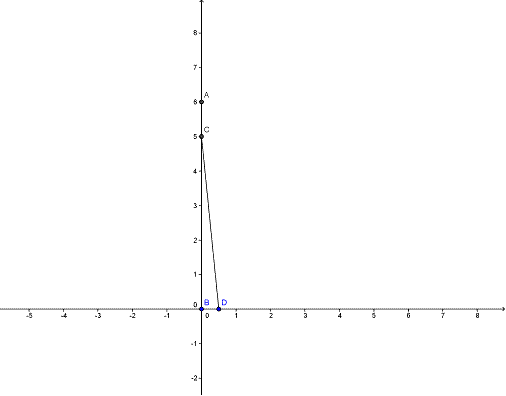
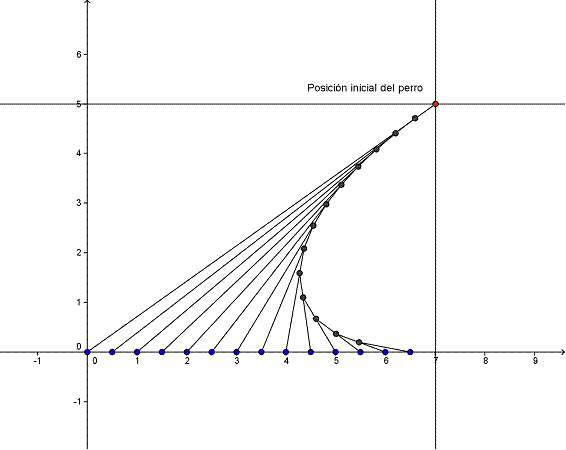
La figura muestra la trayectoria que suele seguir un perro en A, desde el momento en que ve un coche en la posición B. Supongamos que el coche sigue la recta  y=0 a una velocidad constante y, supongamos también, que la velocidad del coche es doble que la del perro.

El camino que recorre el perro lo podemos construir fácilmente. Trazamos la recta que representará la trayectoria del coche. Unimos por una recta los puntos A y B; ésta es la dirección en la que el perro empieza a correr. Pero está claro que ningún  perro puede cambiar fácilmente de dirección dando un salto en el aire, así que se moverá en esta misma dirección durante una corta  distancia AC.

Pero mientras el perro corre de A a C, el coche se desplaza de B a D. Al llegar a C, el perro cambia de dirección hacia el coche, que ahora está en B, y corre en esa dirección mientras el coche se desplaza de D a F.

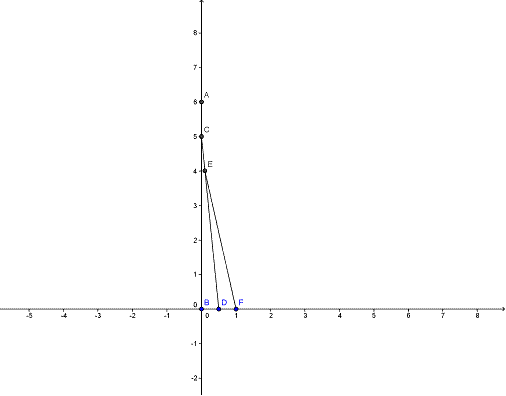
    Repitiendo este proceso se puede ir construyendo la trayectoria que seguirá el perro. Finalmente nos quedará la siguiente curva:

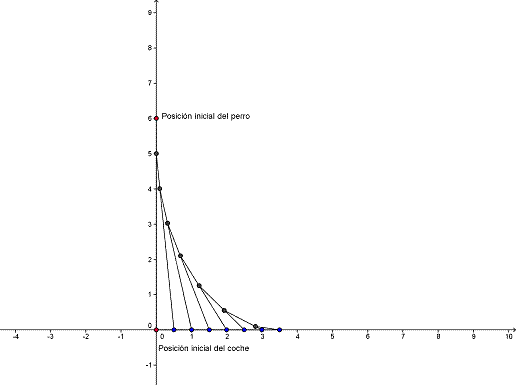
Ejercicio 2

¿Qué ocurre si ambos seres tienen la misma velocidad?

Solución:

    En la posición inicial seleccionada sobre el eje de ordenadas el perseguidor no alcanza su objetivo. Es importante en la construcción de nuestro modelo que todos los elementos dependan de los dos puntos que representan las posiciones iniciales. De esta manera podremos alcanzar también el resultado deseado modificando a nuestra elección ambas posiciones iniciales.

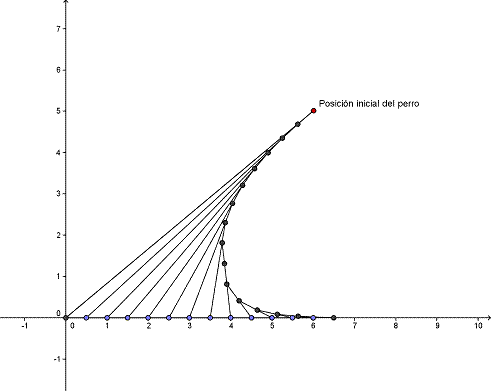
    Otra manera de situar la posición inicial del perro es definiendo el punto A como la intersección de dos rectas: una horizontal y otra vertical. De esta manera nos será muy cómodo colocar al perro en la situación deseada.

Veamos este ejemplo con GeoGebra, pudiendo mover las rectas como queramos:

 

 Página Principal