,
que es un número irracional que proviene de la solución de la ecuación de
segundo grado 
y
es 
.CURIOSIDADES
UN POQUITO DE HISTORIA
Según algunos estudios la investigación de la espiral comienza con los antiguos griegos. La famosa Espiral Equiangular fue descubierta por Descartes en 1638, el cual partió de la propiedad.
Por otra parte Torricelle, que murió en 1647 trabajó en el estudio de estas curvas de forma independiente y empleó el hecho de que el radio está en progresión geométrica según se aumenta el ángulo uniformemente, de lo que dedujo la relación.
Pero fue Bernouilli, unos 50 años después, quien encontró las propiedades de auto-reproducción de la curva.
CONSTRUCCIÓN DE LA ESPIRAL EQUIANGULAR GEOMÉTRICAMENTE
¿No te has preguntado como se puede construir la espiral equiangular geométricamente?
Para ello únicamente has de conocer:
·
El número áureo, llamado
,
que es un número irracional que proviene de la solución de la ecuación de
segundo grado y
es .
Con estas pequeñas indicaciones podrás descubrir la construcción de la espiral equiangular, que es la siguiente:
Si tomamos un rectángulo áureo ABCD (en el que sus lados están en razón áurea, es decir, si b y h son los lados del rectángulo, b/h = Φ) y le sustraemos el cuadrado AEFD cuyo lado es el lado menor AD del rectángulo, resulta que el rectángulo EBCF es áureo. Si después a éste le quitamos el cuadrado EBGH, el rectángulo resultante HGCF también es áureo. Este proceso se puede reproducir indefinidamente, obteniéndose una sucesión de rectángulos áureos encajados que convergen hacia el vértice O de una espiral logarítmica, como puedes ver en el dibujo:
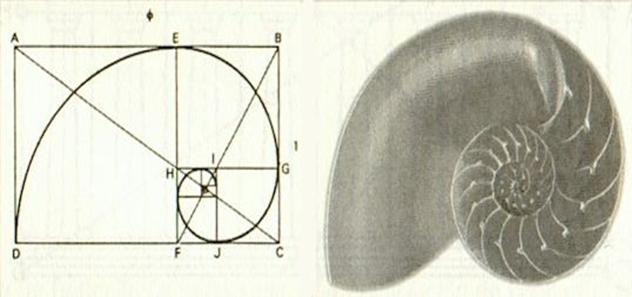
Esta espiral está presente en el crecimiento armónico de muchas formas vegetales (flores y frutos) y animales (conchas de moluscos), aquellas en las que la forma se mantiene invariante. El ejemplo más visualmente representativo es la concha del nautilus.
Esta curva ha cautivado, por su belleza y propiedades, la atención de matemáticos, artistas y naturalistas. De hecho, el matemático Bernoulli, fascinado por sus encantos, la llamó spira mirabilis, rogando que fuera grabada en su tumba.
LA ESPIRAL EQUIANGULAR Y EL ARTE
Esta espiral también se conoce como espiral de Durero por la siguiente historia:
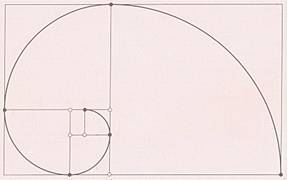
En 1525, tres años antes de morir, el genial pintor renacentista y gran enamorado de las Matemáticas, Alberto Durero (1471-1528) publica una obra titulada Instrucción sobre la medida con regla y compás de figuras planas y sólidas. Es un libro en el que pretende enseñar a los artistas, pintores y matemáticos de la época diversos métodos para trazar diversas figuras geométricas.
En esta obra Durero muestra cómo trazar con regla y compás algunas espirales y entre ellas una que pasará a la historia con su nombre: la Espiral de Durero.
Los rectángulos que se utilizan para la construcción de esta espiral, de los que hemos hablado antes y que tienen proporción áurea también se han utilizado en la pintura, como podemos ver en el siguiente cuadro de la Gioconda, pintado por Leonardo da Vinci:
