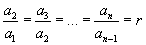Nociones Básicas:

 

Progresiones geométricas

 
Una progresión geométrica es una sucesión en la que cada término se obtiene multiplicando el anterior por un número fijo, que se llama razón de la progresión.

Dicho de otro modo, en una progresión geométrica el cociente entre cada término y el término anterior es una constante r, que se llama razón de la progresión.
 

 

 

 
Ejemplos.
La sucesión 3,6,12,24,48,...... es una progresión geométrica de razón 2.
 La sucesión 0,0.1,0.01,0.001,...... es una progresión geométrica de razón 0.1.
La sucesión 1,1/4,1/16,1/64,....... es una progresión geométrica  de  razón 1/4.

 Término general

Nos interesa disponer de una fórmula que permita calcular el valor de cualquier término de la progresión, si se conocen su primer término a1 y la razón r.
 Por definición de progresión geométrica, es:
            
            a2 = a1·r        a3 = a2·r = (a1·r )·r = a1·r2         a4 = a3·r = (a1·r2 )·r = a1·r3

Y, en general,  an = a1·rn-1 , que es la fórmula del término general de la progresión.

 

Suma de los términos de una progresión geométrica de razón -1 < r < 1

 

                    Si r es un número mayor que -1 y menor que 1, rn se aproxima tanto más a cero cuanto más grande sea n;                     matemáticamente esto se expresa diciendo que rn tiende a cero.

 

                    Obsérvese cómo, por ejemplo,  (1/2)2 = 1/4 = 0,25

                                                                 (1/2)3 = 1/8 = 0,125

                                                                 (1/2)4 = 1/16 = 0,0625

                                                               ...............................................

 

                                                               (1/2)20 = 1/1048576 = 0,0000009

 

                    Y de igual modo        (-1/2)2 = 1/4 = 0,25

                                                    (-1/2)3 = 1/8 = -0,125

                                                    (-1/2)4 = 1/16 = 0,0625

                                                    ................................................

 

                                                    (-1/2)20 = 1/1048576 = 0,0000009

                 

                       

                    Es decir, se comprueba que converge si y sólo si el valor absoluto de la razón es menor que 1; si esto no ocurre, la serie diverge. Si la serie converge, el límite S es igual a

                                           'Matemáticas'
 

                    El símbolo 'Matemáticas'
                    se lee como "límite de Sn cuando n tiende hacia infinito".

                    Las series y progresiones geométricas tienen muchas aplicaciones en las ciencias físicas, biológicas y sociales, y también en cálculos bancarios y financieros.