


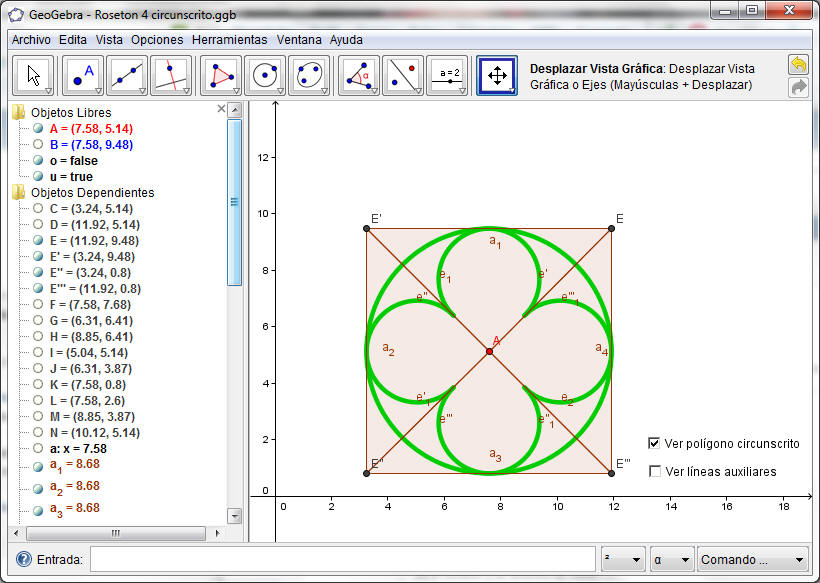
El resultado de esta actividad es el siguiente:
Para empezar a realizar esta actividad, abrimos un archivo de Geogebra y comenzamos dibujando la circunferencia exterior con centro cualquier punto y radio la distancia que nosotros queramos.
Después, dividimos la circunferencia en cuatro cuadrantes puesto que el rosetón que queremos dibujar posee 4 lóbulos. Sobre el primer cuadrante, construimos un cuadrado con lado el radio de la circunferencia exterior ya construido al principio. Hallamos la diagonal de ese cuadrado que formará uno de los lados de un triángulo isósceles cuya base es el doble de la distancia del cuadrado hallado.
De los dos ángulos que posee iguales el triángulo isósceles, hallamos la bisectriz de uno de ellos. Esta bisectriz cortará a la altura del triángulo isósceles en un punto que será el centro de una de las 4 circunferencias interiores que componen los 4 lóbulos.
La circunferencia interior recién hallada tendrá dos puntos de intersección con los lados del triángulo isósceles. Dichos puntos serán los extremos del arco de circunferencia con centro el mismo que la circunferencia interior hallada anteriormente.
Realizando el procedimiento anterior en los tres cuadrantes restantes, obtenemos los 4 lóbulos del rosetón, que junto con la circunferencia inicial del ejercicio forman nuestro rosetón de 4 lóbulos.
Al igual que en la actividad 1, podemos insertar unas casillas de control para ocultar objetos con la intención de poner nuestro dibujo con mucha más claridad ocultando nuestros procedimientos auxiliares.
En el siguiente enlace se encuentra la resolución exacta de esta actividad:
Rosetón_4_lóbulos_circunscrito_geogebra.html