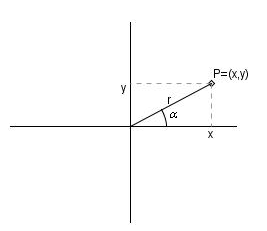Todo punto del plano complejo (plano cartesiano) puede representarse con sus coordenadas (x, y). Estas coordenadas se denominan coordenadas rectangulares o cartesianas. Hay curvas cuya ecuación cartesiana es muy complicada de hallar, pero por suerte esta forma de asignar coordenadas a los puntos del plano no es la única (de hecho en muchas ocasiones ni siquiera es la más aconsejable). Vamos a ver otra manera de asignar coordenadas a los puntos del plano: las coordenadas polares.

Coordenadas Polares

A todo punto P del plano cuyas coordenadas cartesianas son (x, y) podemos asignarle las siguientes coordenadas,

Representado gráficamente sería así:

Teniendo en cuenta esta definición, se tiene que 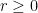y 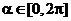 (aunque se puede definir también el ángulo en el intervalo [-π ,π]).

Las ecuaciones que relacionan las coordenadas cartesianas con las polares son las siguientes:

Sobre la expresión del ángulo en función de las coordenadas cartesianas se debe realizar un apunte importante. La función arctan(x) da como resultado dos valores distintos, dos ángulos en cuadrantes opuestos (primero y tercero o segundo y cuarto). Por tanto hay veces en las que al calcular el ángulo puede que obtengamos un resultado incorrecto (puede que nos aparezca el ángulo del cuadrante incorrecto). La regla para el ángulo es la siguiente:

Calculamos el ángulo α  (con la calculadora o con la ayuda del cuadro de las razones trigonométricas) y miramos los signos de las coordenadas (x, y) para ver en qué cuadrante está situado el punto P. Si el ángulo que hemos obtenido está en el mismo cuadrante que P el ángulo obtenido es el correcto. Si no es así sumamos o restamos π al ángulo que nos ha salido cuidando que el resultado de esa suma/resta quede dentro del intervalo [0, 2 π]. Por ejemplo, si obtenemos el ángulo π /3 (que está en el primer cuadrante) y vemos que nuestro punto está en el tercer cuadrante (coordenadas (x, y) negativas) sumamos π al ángulo obtenido, resultando entonces que el α buscado es 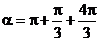      (si en vez de sumar restáramos nos saldríamos de [0, 2 π]).

 

Aplicaciones

Las coordenadas polares son enormemente interesantes al estudiar fenómenos relacionados con distancias y ángulos (a grandes rasgos se podría decir que interesan a la hora de estudiar conceptos relacionados con elipses y circunferencias). Vamos a enumerar unos cuantos:

• Cálculo de límites dobles
• Ecuaciones de curvas: las coordenadas polares simplifican la expresión de las ecuaciones de ciertas curvas. Por ejemplo, la circunferencia de centro (0, 0) y radio 3 tiene a como ecuación en coordenadas cartesianas y a r = 3 como ecuación en polares.
• Forma polar de un número complejo
• Cálculo de integrales dobles
• Navegación marítima
• Cálculos orbitales

Un toque de humor

Las coordenadas polares también sirven para darle un toque de humor matemático a nuestra vida:

¿Qué es un oso polar?
Un oso cartesiano al que se le ha aplicado un cambio de coordenadas.