Este módulo trata de estudiar algunas de las relaciones entre las Matemáticas y las bicicletas.
Inicialmente lo planteamos para los primeros cursos de la E.S.O, pues los conocimientos requeridos (sobre rectas principalmente) eran de un nivel básico.
La Actividad 1 consiste en encontrar la relación entre la velocidad de la bicicleta y el esfuerzo necesario al pedalear y la relación de marchas. Esto se hará utilizando tanto pendientes de rectas como razones.
El contenido era demasiado básico para lo que necesitábamos, y pensamos de qué forma podíamos ampliarlo para que pudiese ser puesto en práctica con alumnos de bachillerato. La idea surgió cuando, guiadas por la profesora, visitamos la página web http://roble.pntic.mec.es/jarran2/geogebra/index.html, donde aparecían muchas modelizaciones matemáticas hechas con GeoGebra. Puesto que se nos encargó este módulo para modelizar con GeoGebra, pensamos buscar nuevas ideas en esta página.
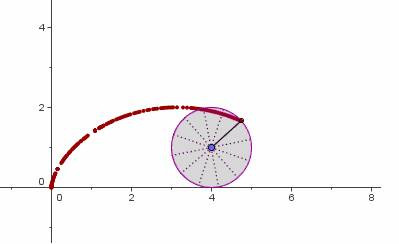
En ella encontramos la curva cicloide. La curva cicloide es la originada por un punto de una circunferencia que se desplaza girando sobre una recta horizontal. Vimos la relación de esta curva con nuestra bicicleta, ya que la rueda es una circunferencia que se moverá sobre una recta horizontal: la carretera. Si pegamos un trozo de cinta adhesiva en el extremo de uno de los radios de la bici y observamos el rastro que va dejando, se ve la curva cicloide.

La curva cicloide se trabajará en la Actividad 2. Después de una introducción, aprovechamos para introducir las coordenadas polares y comentar algunas de sus utilidades. El trabajo de los alumnos consistirá en varias tareas. Por una parte, calcular las ecuaciones de la cicloide, y utilizarlas para construir dicha curva en GeoGebra. Por otra, tendrán que utilizar integrales para calcular la longitud de la curva y el área que queda bajo ella (hasta que llega de nuevo a la recta horizontal).
Aún se podría elevar más el nivel de este módulo viendo que la evoluta (la envolvente de las rectas normales) es otra cicloide, pero esto ya está más indicado para cursos universitarios.
Objetivos del módulo
- Adquirir y conocer nuevas formas de enseñar matemáticas.
- Usar distintos recursos para la adquisición de conocimientos y trabajo de actividades.
- Reconocer y hacer un uso correcto de los conceptos recta, pendiente y razón.
- Conocer GeoGebra como un programa para realizar construcciones tanto sencillas como más complejas, a partir de puntos, rectas, segmentos, vectores...
- Captar la atención de los alumnos a través del uso de las nuevas tecnologías.
- Fomentar la relación entre ecuaciones paramétricas y las polares.
Con este módulo pretendemos que los chicos se familiaricen con el lenguaje propio de la bicicleta y sepan relacionarlo con las matemáticas.
La primera parte trata más de utilizar aspectos sencillos de la Matemática para aplicarlos a su vida cotidiana, mientras que la segunda parte tiene un carácter más teórico.
Estos aspectos no suelen estudiarse actualmente en los institutos. La primera parte implica experimentar con una bicicleta. Las clases en un instituto suelen consistir en un profesor escribiendo en la pizarra y unos alumnos copiando desde sus mesas. La segunda parte consiste en estudiar un fenómeno de la realizad para obtener unas ecuaciones, y utilizar el significado de integral para realizar algunos cálculos. En los libros de texto lo que suele aparecer son ejercicios del tipo: "Calcula la integral de la función f(x) = …", de forma totalmente abstracta.
En general, con este módulo hemos intentado que los alumnos trabajasen las Matemáticas no desde ejercicios simples e independientes de los libros de texto, sino partiendo de la realidad y trabajando el tema de las bicicletas con relativa profundidad, ayudándose para ello de las nuevas tecnologías.