- Lo primero que tenemos que hallar es el dominio.

         Dom f =

- No es una función par, ni impar, ni periódica.

- Asíntotas.

         A.V.

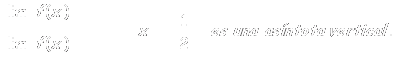
         A.H.

         No tiene

         A.O.

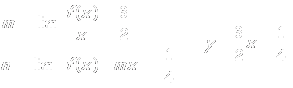          Es la asíntota oblicua.

- Es continua en todo su dominio.

- Veamos la monotonía y puntos singulares. Para ello primero calculamos su derivada.

El denominador se hace 0 para , pero este valor no está en el dominio.

Igualando la derivada a 0 sacaremos los posibles puntos singulares.

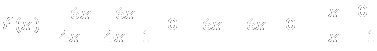
Miramos los signos de f’:

Entonces, f es creciente en el intervalo  y es        decreciente en .

También podemos decir que la función tiene un máximo en x=-1, el punto (-1,-2) es el máximo, y tiene un mínimo en x=0, en el punto (0,1).

- Curvatura y puntos de inflexión. Vamos a necesitar la segunda derivada:

Igualando a cero,

Entonces, f es convexa en (-∞,-1/2) y cóncava en xє (-1/2, ∞). No tiene punto de inflexión ya que  no está en el dominio.

Con este estudio, ya podemos hacer la representación gráfica, que quedaría: