

Para los alumnos, comprender el concepto de función es más complicado de lo que muchos diseñadores de currículum y profesores asumen. Por norma general, los alumnos son incapaces de ver las funciones como aplicaciones de un conjunto de valores de partida a otro de valores de llegada. Para ellos, las funciones son básicamente expresiones algebraicas.
Lo interesante sería que comprendieran el significado más general de lo que es una función, para después particularizar a las funciones reales de variable real que pueden expresarse por medio de una ecuación.
El objetivo de este módulo de aprendizaje es el de acercar las funciones, y sus gráficas, a los alumnos, así como el de reforzar los conocimientos aprendidos en el aula. Como puedes observar, lo hemos divido en dos bloques: ESO y Bachillerato.
El primer contacto de los alumnos con las funciones se produce en la ESO; por esta razón hemos utilizado un lenguaje claro y sencillo a la hora de hablarles del concepto y propiedades de las funciones, tratando así la teoría de un modo intuitivo, apoyándonos en las representaciones gráficas de éstas para que aprendan a interpretarlas.
En el segundo bloque, enfocado hacia el alumnado de Bachillerato, damos una paso más: ahondamos en el análisis de las funciones, haciendo un estudio exhaustivo de estas para posteriormente poder representarlas gráficamente.
Finalizamos cada bloque con una serie de problemas. En el caso de la ESO nos hemos centrado en la interpretación gráfica de funciones, para una futura aplicación en la vida cotidiana. En el bloque de Bachillerato, nos centramos en un tipo de problemas que no suelen encontrarse en los libros de texto.
Desde nuestra experiencia como actuales alumnas, que seguimos siendo receptoras de conocimiento, y nuestra experiencia docente dando clases a alumnos con problemas de aprendizaje matemático, hemos llegado a la conclusión de que este es el enfoque más adecuado que podíamos darle a un módulo de aprendizaje sobre funciones y gráficas.
En esta guía del profesor hemos recopilado una serie de errores que creemos que se repiten con frecuencia entre los alumnos, así como una serie de recomendaciones para que el profesor pueda evitar que se cometan.
Ver las funciones como dos expresiones separadas por un signo de igual, lo que lleva a confundir funciones algebraicamente definidas con ecuaciones. Para evitar este error, por ejemplo, podemos hacer uso del concepto de polinomio y ecuación polinómica enfatizando la diferencia.
polinomio (función) → igualando a 0 → ecuación
Confundir el significado de f(x+a) con f(x)+a, tanto analítica como geométricamente.
x+a → f(x+a)
x → f(x) → f(x)+a
En el primer caso los valores que se ven afectados son los de partida, por lo que geométricamente se traslada la gráfica de f(x) por el eje OX; sin embargo, en el segundo caso los valores afectados son los de llegada, por lo que la traslación se produce en el eje OY.
Creer que a cada x le corresponde una y diferente. Por ejemplo, piensan que las funciones constantes y=a, no son funciones porque el conjunto de llegada está formado por un único punto. Para evitar esta creencia sería conveniente, desde un primer momento, hacerles tomar contacto con funciones no inyectivas.
Creer que las funciones se comportan bien en algún sentido. Por ejemplo, piensan que
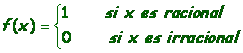
no es una función. Este error se debe a que no se hace hincapié en el concepto general de función.
Pensar que cualquier función que tenga forma de U será cuadrática. Esto ocurre porque en el currículum de la ESO se le da mucha importancia a las parábolas.
Dificultad para relacionar propiedades físicas con gráficas de funciones. Por ejemplo, dada la gráfica
interpretan el punto de corte de las gráficas como el momento y lugar donde se cruzan ambos coches. Esto es debido a que, por una parte están más familiarizados con la relación espacio-tiempo, y por otra, tienen el error conceptual de "gráfica=dibujo", consistente en pensar que las gráficas dadas representan los recorridos que hacen los coches.
No ver la relación entre algunas funciones y otros conceptos anteriormente aprendidos. Por ejemplo, al trabajar con la función y=x2 (con x>0) no son conscientes de que están trabajando con el área de un cuadrado de lado x.
No saber lo que significa cada símbolo en una función algebraicamente definida. Por ejemplo, dada la expresión f(x)=3x, f es el nombre de la función, (x) el valor de partida y 3x el valor de llegada.
No comprender el significado de la composición de funciones. Esto es debido a no ver las funciones como aplicaciones que llevan un valor de partida a otro de llegada.
No entender el significado e importancia de la función inversa, como consecuencia del punto anterior; de hecho, calculan funciones inversas de forma mecánica (métodos a y b del gráfico).
El sistema educativo ha evolucionado en los últimos años hacia una enseñanza más cercana y accesible para los alumnos. Dicha evolución requiere una adaptación del profesor: atrás quedaron las clases magistrales en las que el profesor llegaba a clase, explicaba la lección y se marchaba.
En este punto recopilamos una serie de hábitos que creemos que sería conveniente que el profesor de hoy en día adquiriera.
A diferencia del profesor tradicional, el profesor de hoy en día invierte una parte de la clase al diálogo y discusión con el alumno.
Tras una pequeña exposición por parte del profesor, sería conveniente dejar un tiempo de reflexión individual, para después discutir las conclusiones en pequeños grupos, y finalmente acabar con un debate general entre toda la clase:
| Reflexión individual |
→ |
Reflexión
en grupo |
→ |
Debate
general |
→ |
Conclusiones finales |
↓ ↓ ↓
| Primeras
conclusiones |
→ |
Puesta
en común |
→ |
Diálogo y discusión |
→ |
Durante el debate general, el profesor debe:
adquirir el papel de moderador haciendo partícipes a todos los alumnos.
dar pistas cuando se produzcan bloqueos.
valorar todas las opiniones sin imponer sus criterios.
encauzar la discusión cuando crea conveniente.
realizar preguntas que requieran respuestas que vayan más allá de un sí o un no.
ayudar a los alumnos a extraer sus propias conclusiones sin adelantarse a darles la solución del problema planteado.
evitar los cambios de dirección en el transcurso de la discusión.
no decir "sí", "no", "de acuerdo" ni responder las preguntas de los alumnos ya que puede bloquear las ideas del resto.
no hacer muchas preguntas sobre un mismo problema.
Para que el alumno comprenda de manera óptima la materia que se está estudiando, sería adecuado seguir estas pautas:
El aprendizaje así adquirido queda fuertemente arraigado, incluso de manera inconsciente. Podríamos decir que el fin de este proceso es el de que cada alumno vaya formando una cadena en la que cada eslabón constituya un nuevo conocimiento adquirido.
Libros:
Bufanda Mª Paz, Serafín Mansilla (1997). Números. Matemáticas 2, ED. SM. Madrid.
Colera Jiménez, J., Miguel de Guzmán Ozamiz (1999). Bachillerato. Matemáticas 3, ED. ANAYA. Madrid.
Colera Jiménez, J., Miguel de Guzmán Ozamiz (1996). Matemáticas II. COU, ED. ANAYA. Madrid.
Colera Jiménez, J., M. de Guzmán, Mª José Oliveira, S. Fernández (1989). Bachillerato LOGSE. Matemáticas I, ED. ANAYA. Madrid.
Colera Jiménez, J., M. de Guzmán, Mª José Oliveira, I. Gaztelu, J. E. García (1995). Matemáticas. 4B, ED. ANAYA. Madrid.
Colera Jiménez, J., Miguel de Guzmán Ozamiz, A. Salvador (1987). Matemáticas. Bachillerato 1, ED. ANAYA. Madrid.
Colera Jiménez, J., R. García, I. Gaztelu, M. J. Oliveira (2002) Matemáticas 3. Educación Secundaria, ED. ANAYA. Madrid.
Deulofeu, J., Azcárate, C. (1989) Funciones y gráficas. Síntesis. Madrid.
Ruiz Higueras, L. (1998) La noción de función: Análisis epistemológico y didáctico. Universidad de Jaén.
Shell Centre (1990) El Lenguaje de funciones y gráficas. MEC. Servicio Editorial Universidad del País Vasco.
Vizmanos José R., Máximo Anzola (2005). Algoritmo.3 Secundaria, ED. SM. Madrid.
Páginas Web:
Carlson, M.; Oethrtman, M. (2005) Key aspects of knowing and Learning the concept of function, Researcher Sampler, MAA ONLINE, The mathematical Association of America. http://thales.cica.es/rd/Recursos/rd97/UnidadesDidacticas/03-2-u-graficas.html#ACTI_1
http://www.maa.org/t_and_l/sampler/rs_9.html
http://www.satd.uma.es/matap/svera/links/matnetg08.html
http://www.amejor.com/mates/bloques/analisis.htm
Páginas Web de las que hemos obtenido dibujos:
tudor.mh.edu.ro
firewall.blogia.com
Gráficas hechas con Derive.