Full paper in PDF format:
$%S. Alkhatib and V. P. Kostov, The Schur-Szegö composition of real polynomials of degree 2,
Rev. Mat. Complut. 21 (2008), no. 1, 191–206.%$
The Schur-Szegö Composition of Real
Polynomials of Degree 2
Soliman ALKHATIB and Vladimir Petrov KOSTOV
Received: April 16, 2007
Accepted: September 17, 2007
A real polynomial 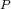 in one real variable is hyperbolic if its roots are all real.
The composition of Schur-Szegö of the polynomials
in one real variable is hyperbolic if its roots are all real.
The composition of Schur-Szegö of the polynomials 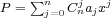 and
and
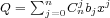 is the polynomial
is the polynomial 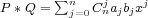 . In the
present paper we show how for
. In the
present paper we show how for  and when
and when 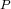 and
and 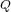 are real or
hyperbolic the roots of
are real or
hyperbolic the roots of  depend on the roots or the coefficients of
depend on the roots or the coefficients of 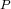 and
and 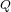 . We consider also the case when
. We consider also the case when 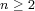 is arbitrary and
is arbitrary and 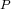 and
and 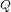 are of the form
are of the form 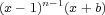 . This case is interesting in the context of
the possibility to present every polynomial having one of its roots at
. This case is interesting in the context of
the possibility to present every polynomial having one of its roots at 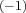 as
a composition of
as
a composition of 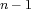 polynomials of the form
polynomials of the form 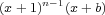 .
.
Key words: composition of Schur-Szegö, hyperbolic polynomial.
2000 Mathematics Subject Classification: 12D10.
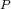 in one real variable is hyperbolic if its roots are all real.
The composition of Schur-Szegö of the polynomials
in one real variable is hyperbolic if its roots are all real.
The composition of Schur-Szegö of the polynomials 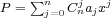 and
and
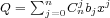 is the polynomial
is the polynomial 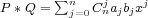 . In the
present paper we show how for
. In the
present paper we show how for  and when
and when 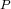 and
and 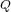 are real or
hyperbolic the roots of
are real or
hyperbolic the roots of  depend on the roots or the coefficients of
depend on the roots or the coefficients of 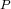 and
and 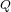 . We consider also the case when
. We consider also the case when 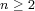 is arbitrary and
is arbitrary and 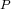 and
and 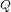 are of the form
are of the form 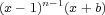 . This case is interesting in the context of
the possibility to present every polynomial having one of its roots at
. This case is interesting in the context of
the possibility to present every polynomial having one of its roots at 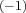 as
a composition of
as
a composition of 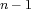 polynomials of the form
polynomials of the form 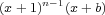 .
.