Full paper in PDF format:
$%I. Asekritova and N. Kruglyak, Invertibility of operators
in spaces of real interpolation, Rev. Mat. Complut. 21 (2008), no. 1, 207–217.%$
Invertibility of Operators
in Spaces of Real Interpolation
Irina ASEKRITOVA and Natan KRUGLYAK
| | Department of Mathematics
Luleå University of Technology
SE-971 87, Luleå — Sweden
natan@ltu.se |
| |
Received: August 18, 2007
Accepted: September 17, 2007
Let 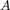 be a linear bounded operator from a couple
be a linear bounded operator from a couple 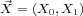 to a
couple
to a
couple 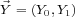 such that the restrictions of
such that the restrictions of 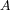 on the spaces
on the spaces 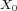 and
and
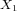 have bounded inverses. This condition does not imply that the restriction
of
have bounded inverses. This condition does not imply that the restriction
of 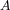 on the real interpolation space
on the real interpolation space 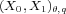 has a bounded inverse for
all values of the parameters
has a bounded inverse for
all values of the parameters  and
and  . In this paper under some conditions
on the kernel of
. In this paper under some conditions
on the kernel of 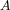 we describe all spaces
we describe all spaces 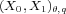 such that the operator
such that the operator
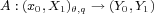 has a bounded inverse.
has a bounded inverse.
Key words: real interpolation, invertible operators.
2000 Mathematics Subject Classification: Primary 46B70, Secondary 46M35.
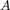 be a linear bounded operator from a couple
be a linear bounded operator from a couple 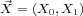 to a
couple
to a
couple 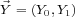 such that the restrictions of
such that the restrictions of 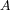 on the spaces
on the spaces 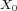 and
and
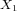 have bounded inverses. This condition does not imply that the restriction
of
have bounded inverses. This condition does not imply that the restriction
of 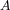 on the real interpolation space
on the real interpolation space 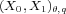 has a bounded inverse for
all values of the parameters
has a bounded inverse for
all values of the parameters  and
and  . In this paper under some conditions
on the kernel of
. In this paper under some conditions
on the kernel of 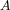 we describe all spaces
we describe all spaces 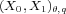 such that the operator
such that the operator
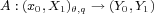 has a bounded inverse.
has a bounded inverse.