Full paper in PDF format:
$%C. M. Edwards and R. V. Hügli, Decoherence in pre-symmetric spaces, Rev. Mat. Complut. 21 (2008),
no. 1, 219–249.%$
Decoherence in Pre-symmetric Spaces
C. Martin EDWARDS and Remo V. HÜGLI
Received: May 14, 2007
Accepted: October 8, 2007
Pre-symmetric complex Banach spaces have been proposed as models for
state spaces of physical systems. A structural projection on a pre-symmetric
space 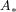 represents an operation on the corresponding system, and has as
its range a further pre-symmetric space which represents the state space of the
resulting system and symmetries of the system are represented by elements of
the group
represents an operation on the corresponding system, and has as
its range a further pre-symmetric space which represents the state space of the
resulting system and symmetries of the system are represented by elements of
the group 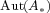 of linear isometries of
of linear isometries of 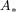 . Two structural projections
. Two structural projections
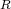 and
and  on the pre-symmetric space
on the pre-symmetric space 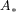 represent decoherent operations
when their ranges are rigidly collinear. It is shown that, for decoherent elements
represent decoherent operations
when their ranges are rigidly collinear. It is shown that, for decoherent elements
 and
and  of
of 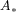 , there exists an involutive element
, there exists an involutive element 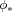 in
in 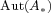 which conjugates the structural projections corresponding to
which conjugates the structural projections corresponding to  and
and  , and
conditions are found for
, and
conditions are found for 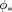 to exchange
to exchange  and
and  . The results are used
to investigate when certain subspaces of
. The results are used
to investigate when certain subspaces of 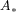 are the ranges of contractive
projections and, therefore, represent systems arising from filtering operations.
are the ranges of contractive
projections and, therefore, represent systems arising from filtering operations.
Key words: JBW -triple, pre-symmetric space, decoherence, involutive grading,
exchange automorphism.
-triple, pre-symmetric space, decoherence, involutive grading,
exchange automorphism.
2000 Mathematics Subject Classification: Primary 46L70; Secondary 17C65, 81P15.
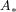 represents an operation on the corresponding system, and has as
its range a further pre-symmetric space which represents the state space of the
resulting system and symmetries of the system are represented by elements of
the group
represents an operation on the corresponding system, and has as
its range a further pre-symmetric space which represents the state space of the
resulting system and symmetries of the system are represented by elements of
the group 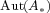 of linear isometries of
of linear isometries of 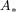 . Two structural projections
. Two structural projections
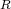 and
and  on the pre-symmetric space
on the pre-symmetric space 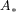 represent decoherent operations
when their ranges are rigidly collinear. It is shown that, for decoherent elements
represent decoherent operations
when their ranges are rigidly collinear. It is shown that, for decoherent elements
 and
and  of
of 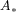 , there exists an involutive element
, there exists an involutive element 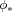 in
in 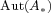 which conjugates the structural projections corresponding to
which conjugates the structural projections corresponding to  and
and  , and
conditions are found for
, and
conditions are found for 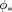 to exchange
to exchange  and
and  . The results are used
to investigate when certain subspaces of
. The results are used
to investigate when certain subspaces of 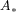 are the ranges of contractive
projections and, therefore, represent systems arising from filtering operations.
are the ranges of contractive
projections and, therefore, represent systems arising from filtering operations.
