$%I. Pop and A. Tofan, Cofibrations and bicofibrations for
 -algebras, Rev. Mat. Complut. 21 (2008), no. 2, 529–552.%$
-algebras, Rev. Mat. Complut. 21 (2008), no. 2, 529–552.%$
Full paper in PDF format:
$%I. Pop and A. Tofan, Cofibrations and bicofibrations
for  -algebras, Rev. Mat. Complut. 21 (2008), no. 2, 529–552.%$
-algebras, Rev. Mat. Complut. 21 (2008), no. 2, 529–552.%$
|
|||||||
ABSTRACT
The paper deals with the correlated concepts of cofibration and bicofibration
in 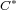 -algebra theory. We study cofibrations of
-algebra theory. We study cofibrations of 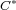 -algebras introduced by
Claude Schochet in (Claude Schochet, Topological methods for
-algebras introduced by
Claude Schochet in (Claude Schochet, Topological methods for
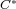 -algebras, III: Axiomatic homology, 1984) [see also (C.
Mohorianu and I. Pop, On the existence of some homotopy commutative
diagrams of *-homomorphisms, 2007)]. Cofibrations are characterized by means
of the mapping cylinder
-algebras, III: Axiomatic homology, 1984) [see also (C.
Mohorianu and I. Pop, On the existence of some homotopy commutative
diagrams of *-homomorphisms, 2007)]. Cofibrations are characterized by means
of the mapping cylinder 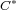 -algebras. We also define and analyze the notion
of bicofibration for
-algebras. We also define and analyze the notion
of bicofibration for 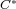 -algebras based on the topological model from (I. Pop,
Bicofibrations, 1980) [see
also (R. W. Kieboom, A bicofibration is just a pair of strictly
separated cofibrations, 1983)]. As an application, an exact sequence of Čerin’s homotopy groups (Z.
Čerin, Homotopy groups for
-algebras based on the topological model from (I. Pop,
Bicofibrations, 1980) [see
also (R. W. Kieboom, A bicofibration is just a pair of strictly
separated cofibrations, 1983)]. As an application, an exact sequence of Čerin’s homotopy groups (Z.
Čerin, Homotopy groups for
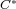 -algebras, 1995), is
obtained.
-algebras, 1995), is
obtained.
Key words:  -algebra, homotopic
-algebra, homotopic  -homomorphisms, cofibration (bicofibration)
of
-homomorphisms, cofibration (bicofibration)
of  -algebras, mapping cylinder (cone), double mapping cylinder, Čerin’s homotopy
groups for
-algebras, mapping cylinder (cone), double mapping cylinder, Čerin’s homotopy
groups for  -algebras.
-algebras.
2000 Mathematics Subject Classification: 46L85, 55P05.