Full paper in PDF format:
$%M. Kabanava, Tempered Radon measures, Rev. Mat. Complut. 21 (2008), no. 2, 553–564.%$
Tempered Radon Measures
Maryia KABANAVA
Received: December 11, 2007
Accepted: January 1, 2008
A tempered Radon measure is a  -finite Radon measure in
-finite Radon measure in 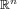 which
generates a tempered distribution. We prove the following assertions. A Radon
measure
which
generates a tempered distribution. We prove the following assertions. A Radon
measure  is tempered if, and only if, there is a real number
is tempered if, and only if, there is a real number  such that
such that
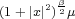 is finite. A Radon measure is finite if, and only if, it belongs to
the positive cone
is finite. A Radon measure is finite if, and only if, it belongs to
the positive cone 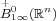 of
of 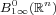 . Then
. Then 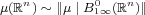 (equivalent norms).
(equivalent norms).
Key words: Radon measure, tempered distributions, Besov spaces.
2000 Mathematics Subject Classification: 42B35, 28C05.
 -finite Radon measure in
-finite Radon measure in 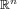 which
generates a tempered distribution. We prove the following assertions. A Radon
measure
which
generates a tempered distribution. We prove the following assertions. A Radon
measure  is tempered if, and only if, there is a real number
is tempered if, and only if, there is a real number  such that
such that
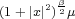 is finite. A Radon measure is finite if, and only if, it belongs to
the positive cone
is finite. A Radon measure is finite if, and only if, it belongs to
the positive cone 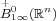 of
of 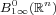 . Then
. Then 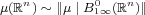 (equivalent norms).
(equivalent norms).