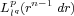 when
when 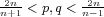 . Here we prove that
there exist weak-type estimates for this operator for the extremal exponents,
that is, it is bounded from
. Here we prove that
there exist weak-type estimates for this operator for the extremal exponents,
that is, it is bounded from 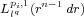 to
to 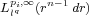 for
for  when
when 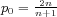 ,
, 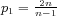 ,
, 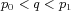 , and we consider radial functions.
, and we consider radial functions.
Full paper in PDF format:
$%E. Romera, Extremal vector vInequalities
for Hankel transforms, Rev. Mat. Complut. 22 (2009), no. 1, 153–163.%$
ABSTRACT
The disc multiplier may be seen as a vector valued operator when we consider
its projections in terms of the spherical harmonics. In this form, it represents a
vector valued Hankel transform. We know that, for radial functions, it is bounded
on the spaces 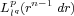 when
when 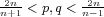 . Here we prove that
there exist weak-type estimates for this operator for the extremal exponents,
that is, it is bounded from
. Here we prove that
there exist weak-type estimates for this operator for the extremal exponents,
that is, it is bounded from 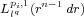 to
to 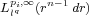 for
for  when
when  ,
, 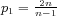 ,
, 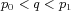 , and we consider radial functions.
, and we consider radial functions.
Key words: disc multiplier, Fourier-Hankel transforms.
2000 Mathematics Subject Classification: 42B10.