Full paper in PDF format:
$%D. Yang, Besov and Triebel-Lizorkin spaces related to singular integrals with
flag kernels,
Rev. Mat. Complut. 22 (2009), no. 1, 253–302.%$
Besov and Triebel-Lizorkin Spaces Related
to Singular Integrals with Flag Kernels
Dachun YANG
School of Mathematical Sciences
Beijing Normal University
Laboratory of Mathematics and Complex Systems
Ministry of Education
Beijing 100875 — People’s Republic of China
dcyang@bnu.edu.cn
Received: August 11, 2008
Accepted: January 8, 2009
Let 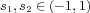 and
and 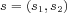 . In this paper, the author introduces
the Besov space
. In this paper, the author introduces
the Besov space 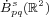 with
with ![p,q ∈[1,∞ ]](vol22-1n3x.png) and the Triebel-Lizorkin
space
and the Triebel-Lizorkin
space 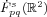 with
with 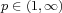 and
and ![q ∈ (1,∞ ]](vol22-1n6x.png) associated to singular
integrals with flag kernels. Some basic properties, including their dual spaces,
some equivalent norm characterizations via Littlewood-Paley functions, lifting
properties and some embedding theorems, on these spaces are given. Moreover,
the author obtains the boundedness of flag singular integrals and fractional
integrals on these spaces.
associated to singular
integrals with flag kernels. Some basic properties, including their dual spaces,
some equivalent norm characterizations via Littlewood-Paley functions, lifting
properties and some embedding theorems, on these spaces are given. Moreover,
the author obtains the boundedness of flag singular integrals and fractional
integrals on these spaces.
Key words: Besov space, Triebel-Lizorkin space, flag singular integral, flag fractional
integral, Littlewood-Paley operator, dual space, lifting, embedding.
2000 Mathematics Subject Classification: 42B35, 42B20, 42B25, 46E35.
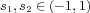 and
and 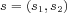 . In this paper, the author introduces
the Besov space
. In this paper, the author introduces
the Besov space 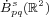 with
with ![p,q ∈[1,∞ ]](vol22-1n3x.png) and the Triebel-Lizorkin
space
and the Triebel-Lizorkin
space 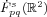 with
with 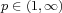 and
and ![q ∈ (1,∞ ]](vol22-1n6x.png) associated to singular
integrals with flag kernels. Some basic properties, including their dual spaces,
some equivalent norm characterizations via Littlewood-Paley functions, lifting
properties and some embedding theorems, on these spaces are given. Moreover,
the author obtains the boundedness of flag singular integrals and fractional
integrals on these spaces.
associated to singular
integrals with flag kernels. Some basic properties, including their dual spaces,
some equivalent norm characterizations via Littlewood-Paley functions, lifting
properties and some embedding theorems, on these spaces are given. Moreover,
the author obtains the boundedness of flag singular integrals and fractional
integrals on these spaces.