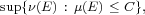 | (1) |
Full paper in PDF:
$%L. R. Berrone,
Coalescence of measures and f-rearrangements of a function, Rev. Mat. Complut. 12 (1999),
no. 2, 477–509.
%$
ABSTRACT
This paper addresses the question of characterizing optimum values in the problem
|
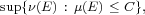| (1) |
where 
and 
are measures defined on a 
-finite measurable space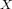 
. With
this purpose, the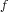 
-rearrangement of a function 
is introduced so as to formalize
the idea of rearranging the level sets of the function 
according to how these sets
are arranged in a given function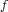 
. A characterization of optima of problem (1) is then
obtained in terms of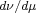 
-rearrangements, 
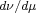being the Radon-Nikodým
derivative of the measure 
with respect to 
. When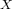 
is a topological space
and 
, 
are Borel measures, we say that 
is coalescent with respect to 
when, for every 
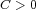, there exist connected optima solving problem (1). A
general criterion for coalescence is given and some simple examples are
discussed.
1991 Mathematics Subject Classification: 49N99, 28A25, 26D10.