Full paper in PDF:
$% I. Vajda, A. Veselý, and J. Zvárová, On the Amount of information resulting from
empirical and theoretical knowledge, Rev. Mat. Complut. 18 (2005), no. 2, 275–283.%$
On the Amount of Information Resulting
from Empirical and Theoretical
Knowledge
Igor VAJDA, Arnošt V
ESELÝ,
and Jana ZVÁROVÁ
EuroMISE Center
Institute of Computer Science
Academy of Sciences of the Czech Republic
CZ-182 07, Prague — Czech Republic
Received: August 26, 2004
Accepted: November 11, 2004
ABSTRACT
We present a mathematical model allowing formally define the concepts of
empirical and theoretical knowledge. The model consists of a finite set 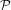 of
predicates and a probability space
of
predicates and a probability space 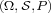 over a finite set
over a finite set  called ontology
which consists of objects
called ontology
which consists of objects  for which the predicates
for which the predicates 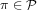 are either valid
(
are either valid
(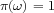 ) or not valid (
) or not valid (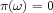 ). Since this is a first step in this area,
our approach is as simple as possible, but still nontrivial, as it is demonstrated
by examples. More realistic approach would be more complicated, based on a
fuzzy logic where the predicates
). Since this is a first step in this area,
our approach is as simple as possible, but still nontrivial, as it is demonstrated
by examples. More realistic approach would be more complicated, based on a
fuzzy logic where the predicates 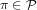 are valid on the objects
are valid on the objects 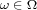 to
some degree (
to
some degree (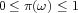 ). We use the classical information divergence to
introduce the amount of information in empirical and theoretical knowledge.
By an example is demonstrated that information in theoretical knowledge is an
extension of the “sematic information” introduced formerly by Bar Hillel and
Carnap as an alternative to the information of Shannon.
). We use the classical information divergence to
introduce the amount of information in empirical and theoretical knowledge.
By an example is demonstrated that information in theoretical knowledge is an
extension of the “sematic information” introduced formerly by Bar Hillel and
Carnap as an alternative to the information of Shannon.
Key words: probability space, ontology, predicate, knowledge area, state of the
knowledge area, empirical knowledge, theoretical knowledge, information in empirical
knowledge, information in theoretical knowledge.
2000 Mathematics Subject Classification: G2B10, 94A17, 94D05.
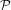 of
predicates and a probability space
of
predicates and a probability space 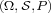 over a finite set
over a finite set  called ontology
which consists of objects
called ontology
which consists of objects  for which the predicates
for which the predicates 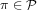 are either valid
(
are either valid
(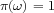 ) or not valid (
) or not valid (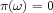 ). Since this is a first step in this area,
our approach is as simple as possible, but still nontrivial, as it is demonstrated
by examples. More realistic approach would be more complicated, based on a
fuzzy logic where the predicates
). Since this is a first step in this area,
our approach is as simple as possible, but still nontrivial, as it is demonstrated
by examples. More realistic approach would be more complicated, based on a
fuzzy logic where the predicates 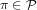 are valid on the objects
are valid on the objects 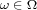 to
some degree (
to
some degree (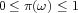 ). We use the classical information divergence to
introduce the amount of information in empirical and theoretical knowledge.
By an example is demonstrated that information in theoretical knowledge is an
extension of the “sematic information” introduced formerly by Bar Hillel and
Carnap as an alternative to the information of Shannon.
). We use the classical information divergence to
introduce the amount of information in empirical and theoretical knowledge.
By an example is demonstrated that information in theoretical knowledge is an
extension of the “sematic information” introduced formerly by Bar Hillel and
Carnap as an alternative to the information of Shannon.