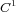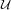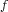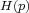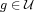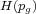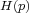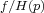Full paper in PDF format:
$% M. J. Pacifico and J. L. Vieitez, Entropy-expansiveness and domination
for surface diffeomorphisms, Rev. Mat. Complut. 21 (2008), no. 2, 293–317.%$
Entropy-Expansiveness and Domination
for Surface Diffeomorphisms
María José PACIFICO and José L. VIEITEZ
| Instituto de Matematica |
| Universidade Federal do Rio de Janeiro |
| C. P. 68.530, CEP 21.945-970 |
| Rio de Janeiro, R. J. — Brazil |
| pacifico@im.ufrj.br |
| | Instituto de Matematica |
| Facultad de Ingenieria |
| Universidad de la Republica |
| CC30, CP 11300 Montevideo — Uruguay |
| jvieitez@fing.edu.uy |
|
| |
|
|
| |
Received:
July 3, 2006
Accepted: March 10, 2007
Let 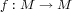 be a
be a  -diffeomorphism,
-diffeomorphism, 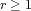 , defined on a closed
manifold
, defined on a closed
manifold 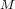 . We prove that if
. We prove that if 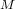 is a surface and
is a surface and 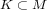 is a compact
invariant set such that
is a compact
invariant set such that 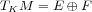 is a dominated splitting then
is a dominated splitting then 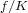 is entropy expansive. Moreover
is entropy expansive. Moreover 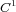 generically in any dimension, isolated
homoclinic classes
generically in any dimension, isolated
homoclinic classes 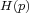 ,
,  hyperbolic, are entropy expansive.
hyperbolic, are entropy expansive.
Conversely, if there exists a 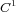 neighborhood
neighborhood 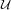 of a surface diffeomorphism
of a surface diffeomorphism
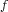 and a homoclinic class
and a homoclinic class 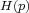 ,
,  hyperbolic, such that for every
hyperbolic, such that for every 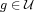 the continuation
the continuation 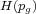 of
of 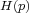 is entropy-expansive then there is a
dominated splitting for
is entropy-expansive then there is a
dominated splitting for 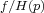 .
.
Key words: entropy-expansiveness, homoclinic classes, dominated splitting, homoclinic
tangency, symbolic extension.
2000 Mathematics Subject Classification: 37D30, 37C29, 37E30.
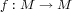 be a
be a  -diffeomorphism,
-diffeomorphism, 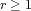 , defined on a closed
manifold
, defined on a closed
manifold 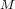 . We prove that if
. We prove that if 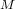 is a surface and
is a surface and 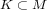 is a compact
invariant set such that
is a compact
invariant set such that 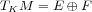 is a dominated splitting then
is a dominated splitting then 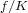 is entropy expansive. Moreover
is entropy expansive. Moreover 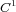 generically in any dimension, isolated
homoclinic classes
generically in any dimension, isolated
homoclinic classes 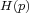 ,
,  hyperbolic, are entropy expansive.
hyperbolic, are entropy expansive.