Full paper in PDF format:
$%C. Cabuzel and A. Piétrus, Solving variational iby a method obtained using a
multipoint iteration formula, Rev. Mat. Complut. 22 (2009), no. 1, 63–74.%$
Solving Variational Inclusions
by a Method Obtained Using a
Multipoint Iteration Formula
Catherine CABUZEL and Alain PIÉTRUS
Laboratoire Analyse, Optimisation, Contrôle
Université des Antilles et de la Guyane
Département de Mathématiques et Informatique
Campus de Fouillole
F-97159 Pointe-à-Pitre — France
catherine.zebre@univ-ag.fr
apietrus@univ-ag.fr
Received: March 26, 2007
Accepted: February 18, 2008
This paper deals
with variational inclusions of the form: 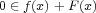 where
where 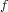 is a single
function admitting a second order Fréchet derivative and
is a single
function admitting a second order Fréchet derivative and  is a set-valued map
acting in Banach spaces. We prove the existence of a sequence
is a set-valued map
acting in Banach spaces. We prove the existence of a sequence 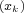 satisfying
satisfying
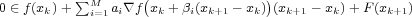 where the single-valued function involved in this relation is an approximation of
the function
where the single-valued function involved in this relation is an approximation of
the function 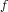 based on a multipoint iteration formula and we show that this
method is locally cubically convergent.
based on a multipoint iteration formula and we show that this
method is locally cubically convergent.
Key words: set-valued mapping, generalized equations, pseudo-Lipschitz maps,
multipoint iteration formula.
2000 Mathematics Subject Classification: 49J53, 47H04, 65K10.
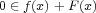 where
where 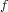 is a single
function admitting a second order Fréchet derivative and
is a single
function admitting a second order Fréchet derivative and  is a set-valued map
acting in Banach spaces. We prove the existence of a sequence
is a set-valued map
acting in Banach spaces. We prove the existence of a sequence 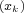 satisfying
satisfying
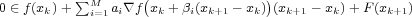 where the single-valued function involved in this relation is an approximation of
the function
where the single-valued function involved in this relation is an approximation of
the function 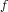 based on a multipoint iteration formula and we show that this
method is locally cubically convergent.
based on a multipoint iteration formula and we show that this
method is locally cubically convergent.