Práctica 5

Contents

Ejercicio 1

Imortante: Para consequir el valor x(2*pi) (es decir t = 2*pi) hay que ajustar el paso h (h = 2*pi, pi, pi/2,...).

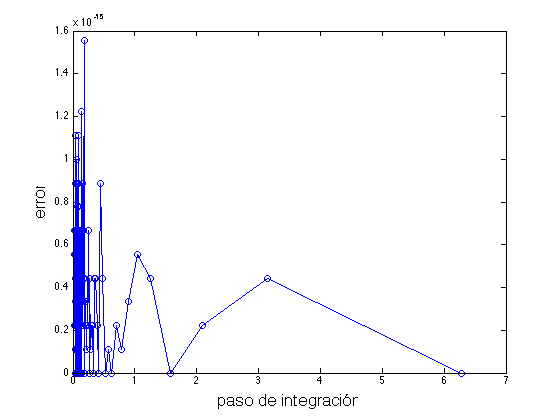
x0 = 1;                     % Condición Inicial
Tinter = [0, 2*pi];         % Intervalo de tiempo
x_exc = 2 - cos(Tinter(2)); % Valor exácto

h = diff(Tinter)./(1:200); % generamos pasos de integración

E = zeros(1,length(h)); % Errores para diferentes h
for k = 1:length(h)
    x = Metodo_Euler(@FuncPrimerEjemplo, x0, h(k), Tinter);
    E(k) = abs(x(end) - x_exc);
end

figure('color','w')
plot(h,E,'o-')
ylabel('error','FontSize',16)
xlabel('paso de integración','FontSize',16)

Ejercicio 2

Función usada:

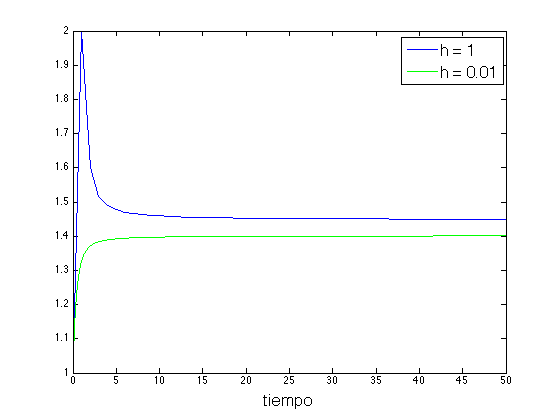
h = [1, 0.01];      % Pasos
x0 = 1;             % Condición Inicial
Tinter = [0, 50];  % Intervalo de tiempo

figure('color','w')
colores = 'bgrcmyk';
leg = cell(1, length(h));
for k = 1:length(h)
    [x, t] = Metodo_Euler(@FuncP5, x0, h(k), Tinter);

    plot(t, x, colores(k));
    hold on
    leg{k} = ['h = ' num2str(h(k))];
end
xlabel('tiempo','FontSize',16)
legend(leg,'FontSize',16)

Ejercicio 3

Función usada:

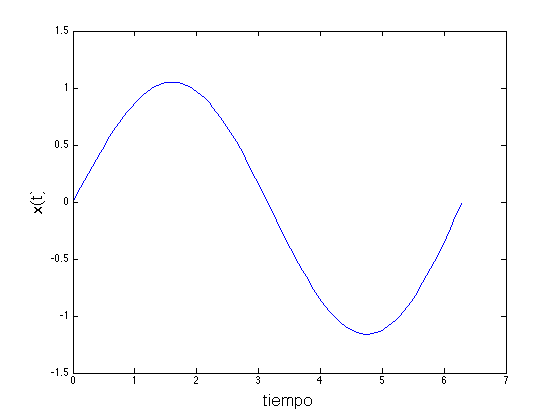
x0 = [0, 1];        % Condición Inicial
Tinter = [0, 2*pi];  % Intervalo de tiempo
h = diff(Tinter)/100;      % Pasos

[x, t] = Metodo_Euler(@FuncP5_2, x0, h, Tinter);

figure('color','w')
plot(t,x(:,1))
xlabel('tiempo','FontSize',16)
ylabel('x(t)','FontSize',16)

Ejercicio 4

Función usada:

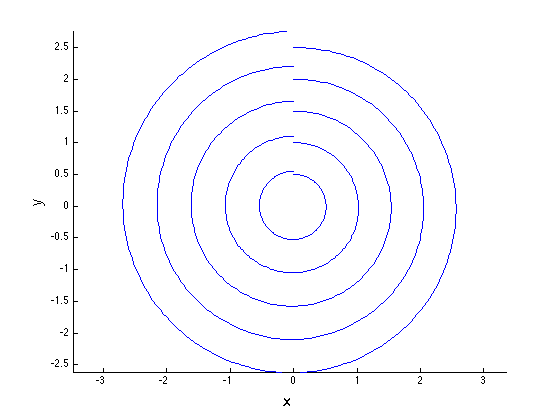
Las soluciones no son periódicas!

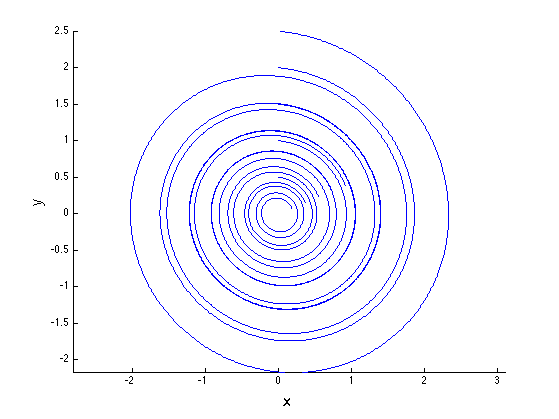
Tinter = [0, 2*pi];  % Intervalo de tiempo
h = diff(Tinter)/200;      % Pasos

y0 = 0.5:0.5:2.5;     % Condiciones iniciales en y
x0 = zeros(size(y0)); % Condiciones iniciales en x

figure('color','w')
hold on
for k = 1:length(y0);
    x = Metodo_Euler(@FuncP5_2, [x0(k) y0(k)], h, Tinter);
    plot(x(:,1),x(:,2))
end
xlabel('x','FontSize',16)
ylabel('y','FontSize',16)
axis equal

Ejercicio 5

Función usada:

Tinter = [0, 20];     % Intervalo de tiempo
h = 0.01;             % Pasos

y0 = 0.5:0.5:2.5;     % Condiciones iniciales en y
x0 = zeros(size(y0)); % Condiciones iniciales en x

figure('color','w')
hold on
for k = 1:length(y0);
    x = Metodo_Euler(@FuncP5_3, [x0(k) y0(k)], h, Tinter);
    plot(x(:,1),x(:,2))
end
xlabel('x','FontSize',16)
ylabel('y','FontSize',16)
axis equal

Published with MATLAB® 7.12