Práctica 7

Contents

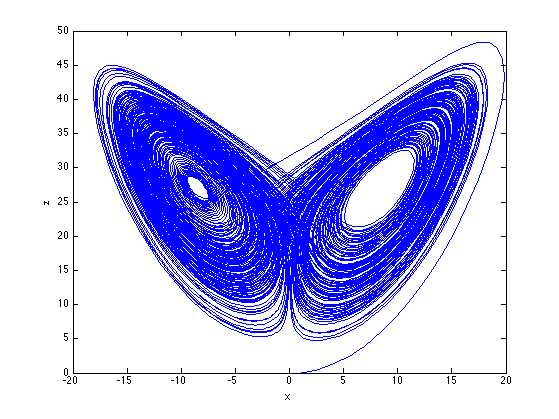
Ejercicio 1

Se usan las funciónes:

x0 = [1,2,0];       % Condición Inicial
Tinter = [0, 200];  % intervalo
h = 0.01;           % Paso

x = Metodo_RK4(@Lorenz, x0, h, Tinter);
figure('color','w')
plot(x(:,1), x(:,3),'b-')
xlabel('x'); ylabel('z');

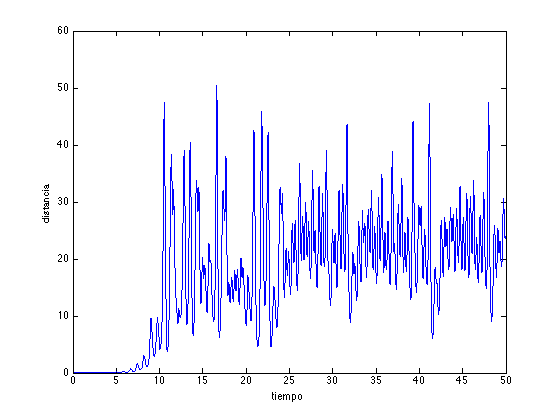
Ejercicio 2

x0a = [40 60 50].*rand(1,3) - [20 30 0];  % Condición Inicial a

phi = 2*pi*rand; teta = 2*pi*rand; r = 0.001*rand;
dxy = r*[sin(teta)*cos(phi) sin(teta)*sin(phi) cos(teta)];
x0b = x0a + dxy;                          % Condición Inicial b

Tinter = [0, 50];  % intervalo
h = 0.02;          % Paso
xa     = Metodo_RK4(@Lorenz, x0a, h, Tinter);  % trayectoria a
[xb,t] = Metodo_RK4(@Lorenz, x0b, h, Tinter);  % trayectoria b
d = sqrt(sum((xa - xb).^2, 2)); % distancia entre las trayectorias

figure('color','w')
plot(t, d,'b-')
xlabel('tiempo'); ylabel('distancia');

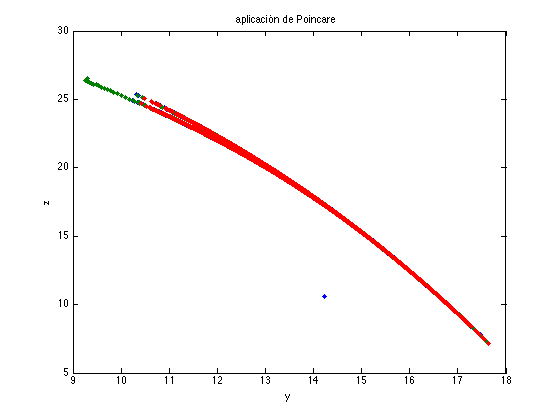
Ejercicio 5

Se usan las funciónes:

Tinter = [0, 10000];  % intervalo
h = 0.01;             % Paso

figure('color','w')
for k = 1:3,
    x0 = [40 60 50].*rand(1,3) - [20 30 0];  % Condición Inicial
    [xyz,t] = Metodo_RK4(@Lorenz, x0, h, Tinter);
    [y,z] = AplicacionPoincare(xyz, sqrt(28*8/3));
    plot(y, z, '.', 'MarkerSize',7)
    hold all
end

xlabel('y'); ylabel('z');
title('aplicación de Poincare')

Published with MATLAB® 7.12