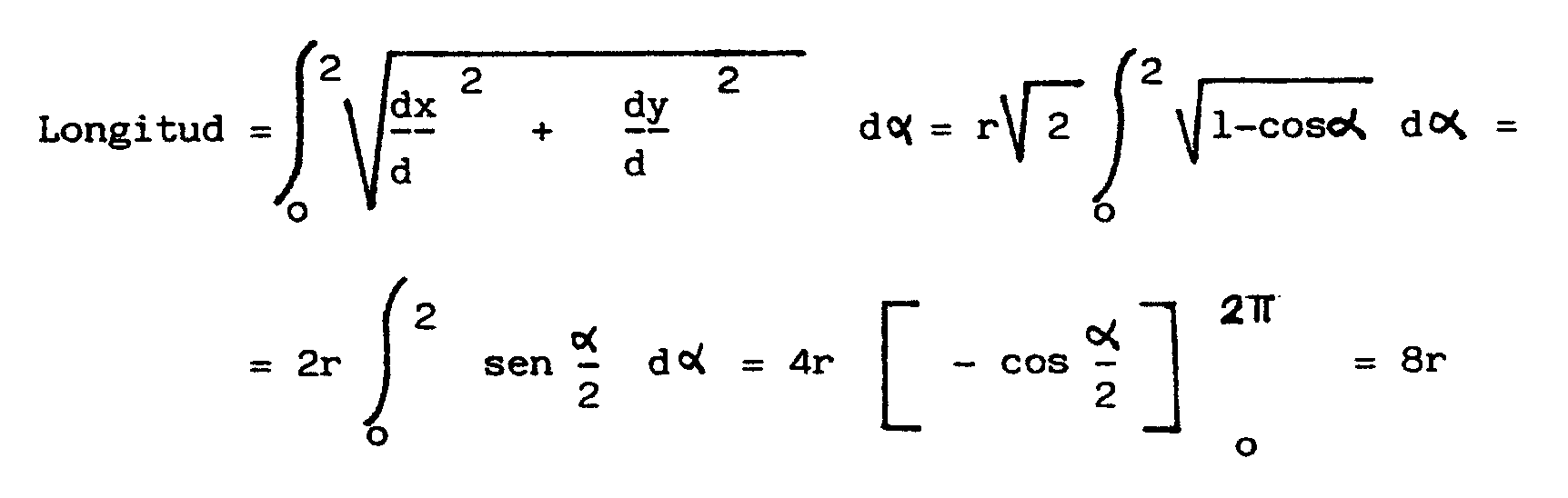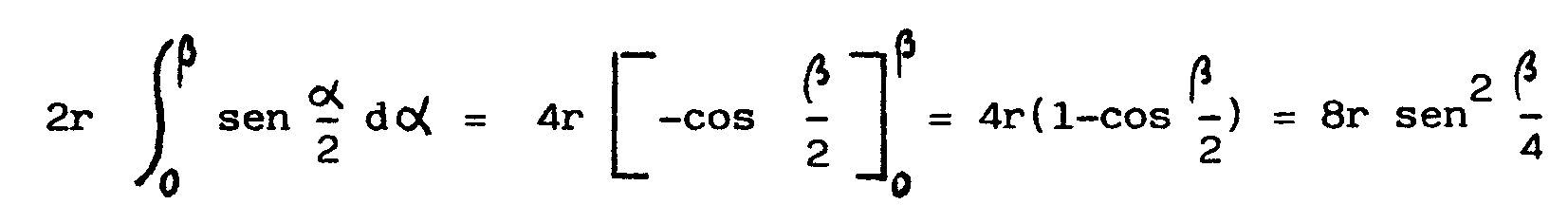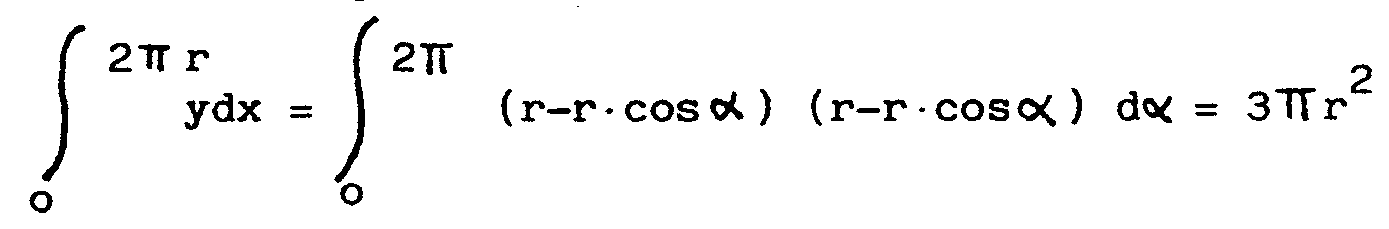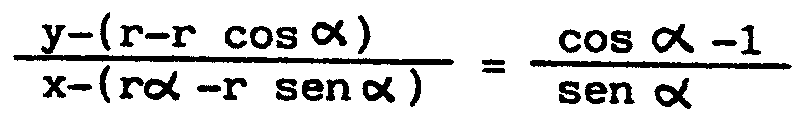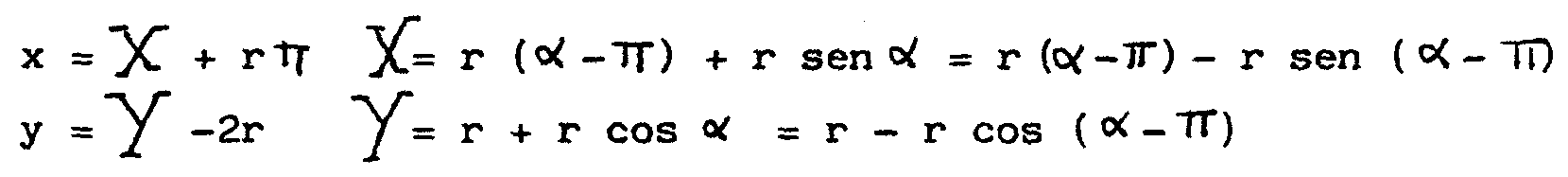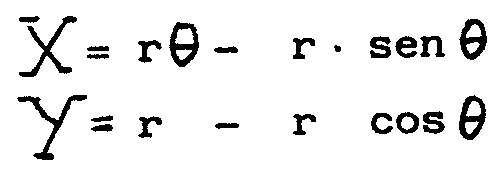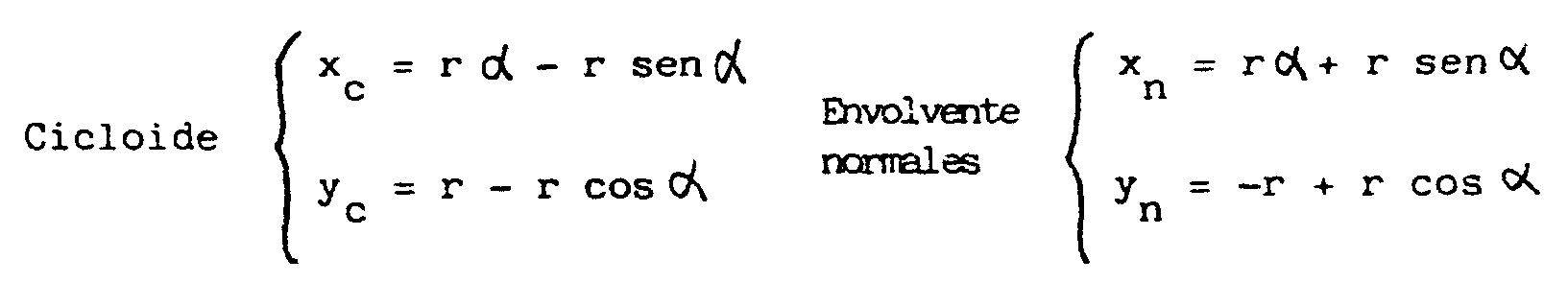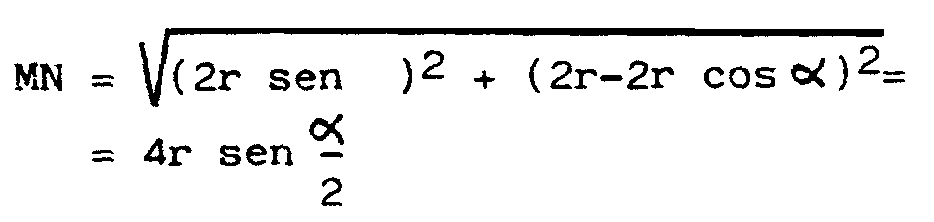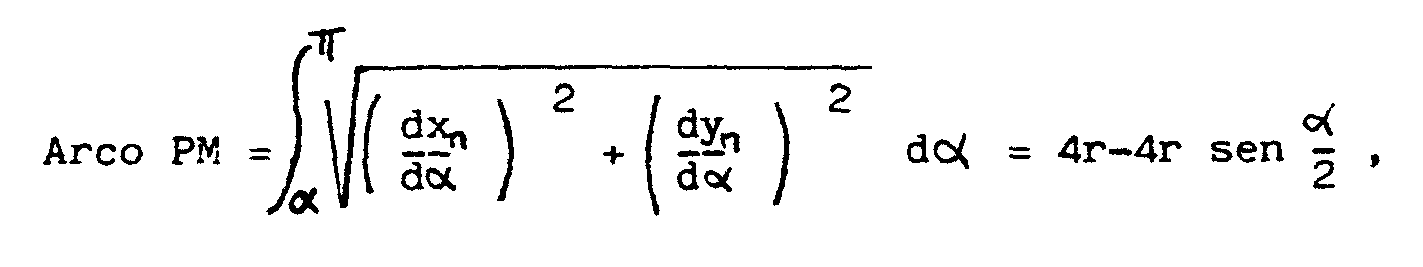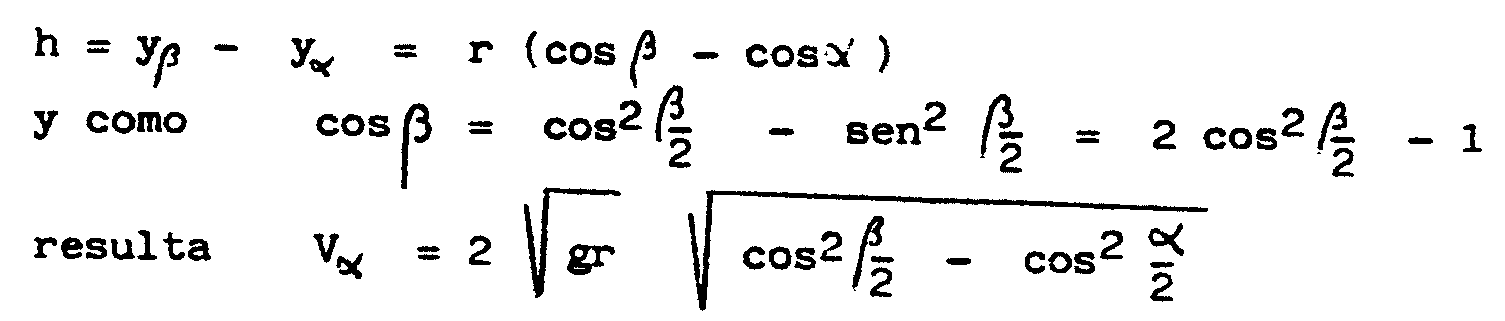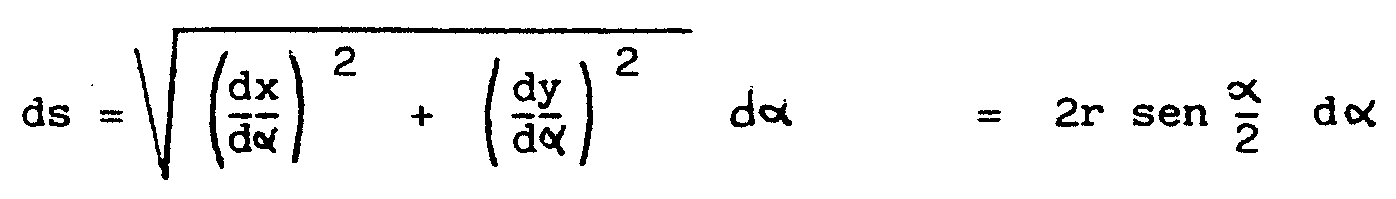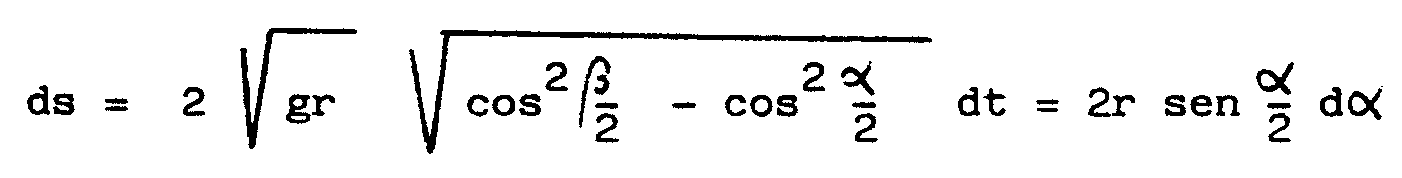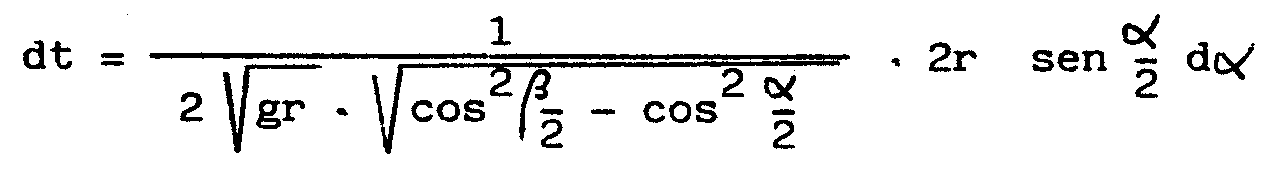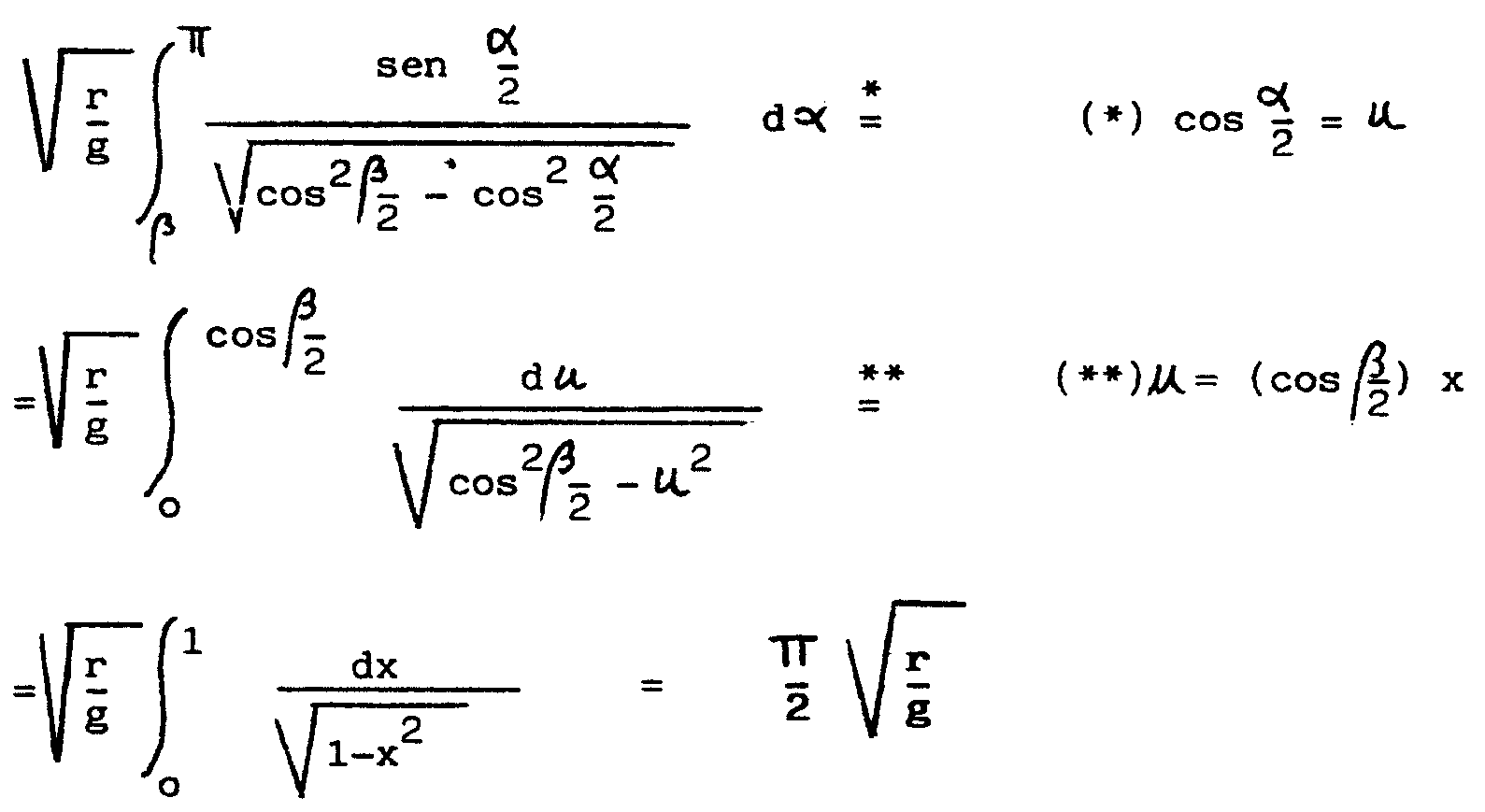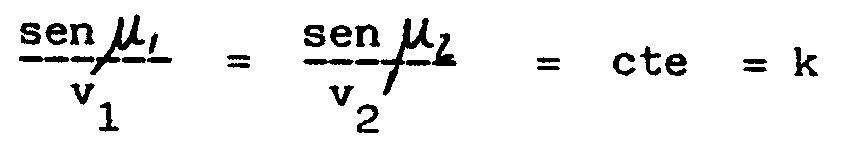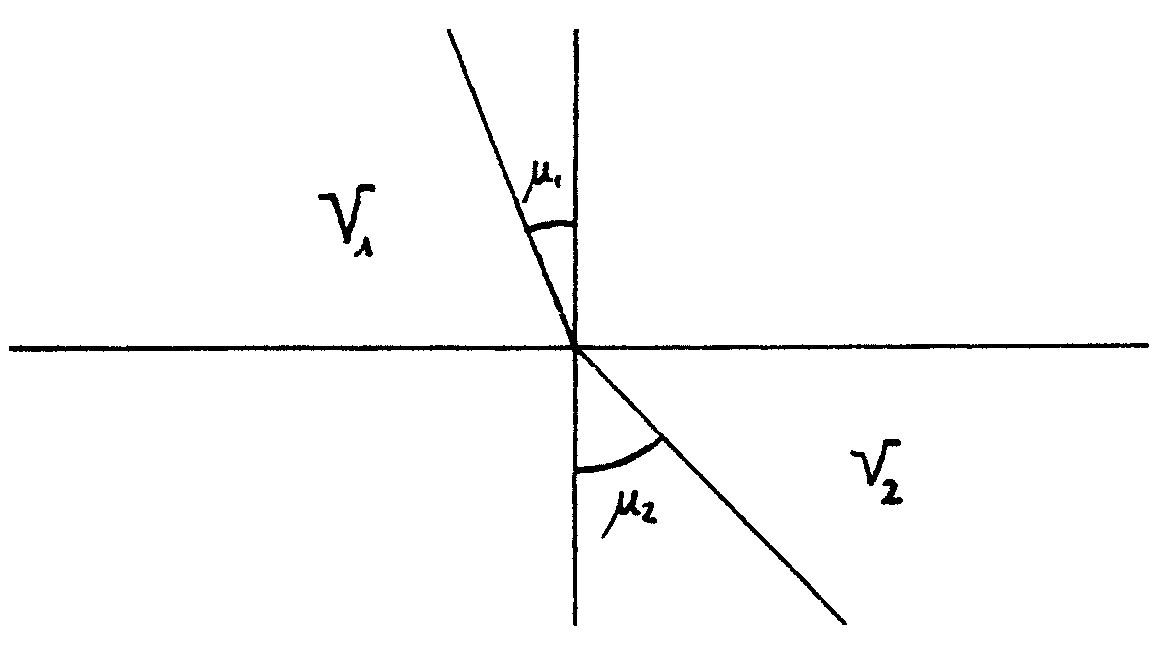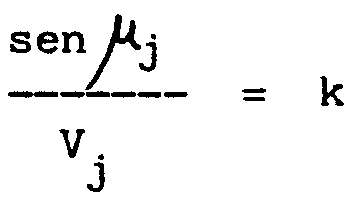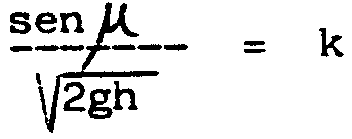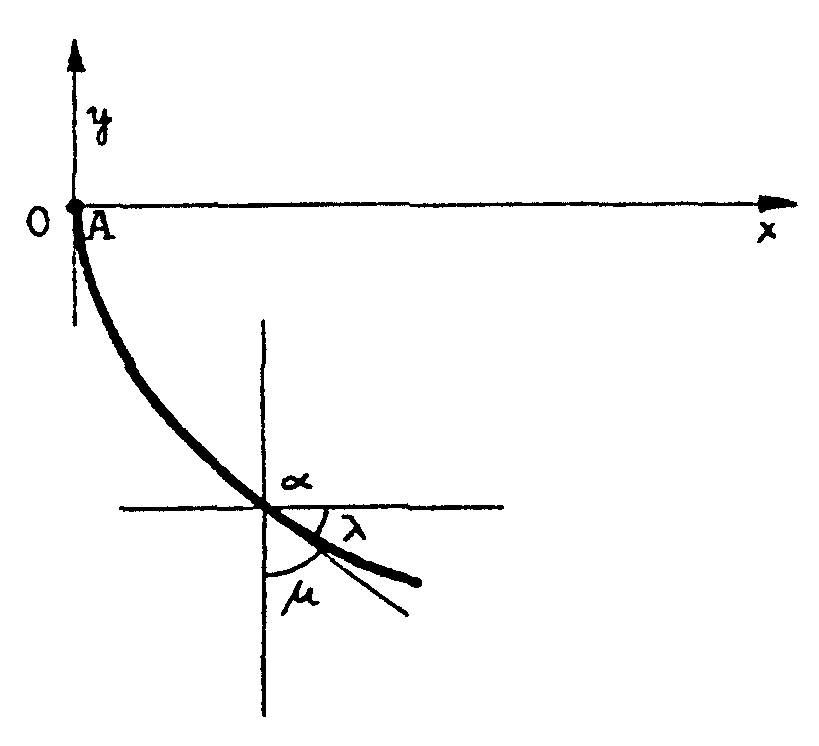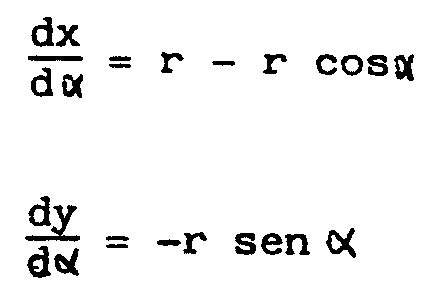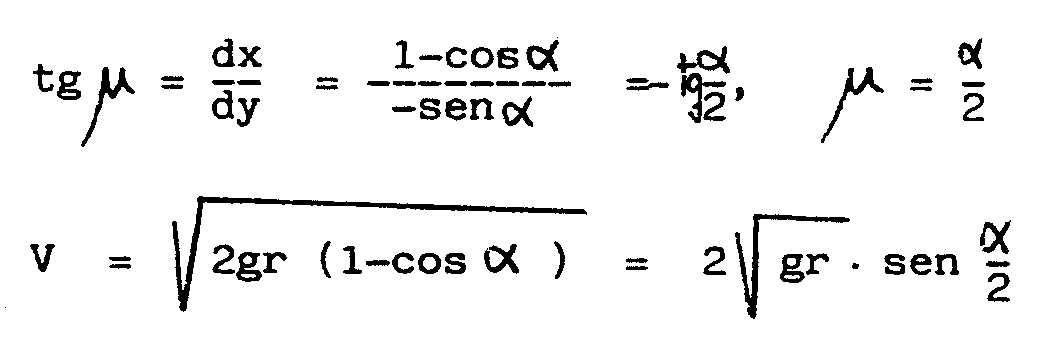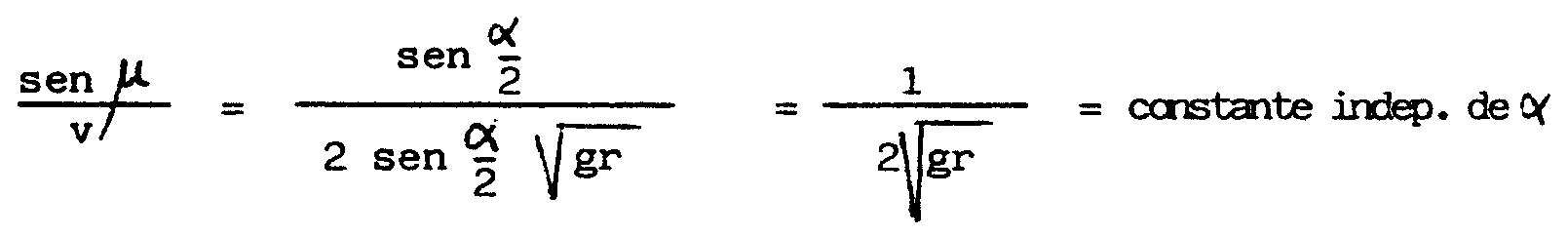ECUACIONES Y DEMOSTRACIONES DE LAS PROPIEDADES DE LA CICLOIDE.             Vamos a ver si nos podemos hacer con la ecuación de la cicloide. Tomemos unos ejes coordenados cómodos, la línea recta donde se apoya la rueda será el eje x y el eje y será la perpendicular a ella por el punto que has señalado en la rueda cuando éste está en el suelo.
   
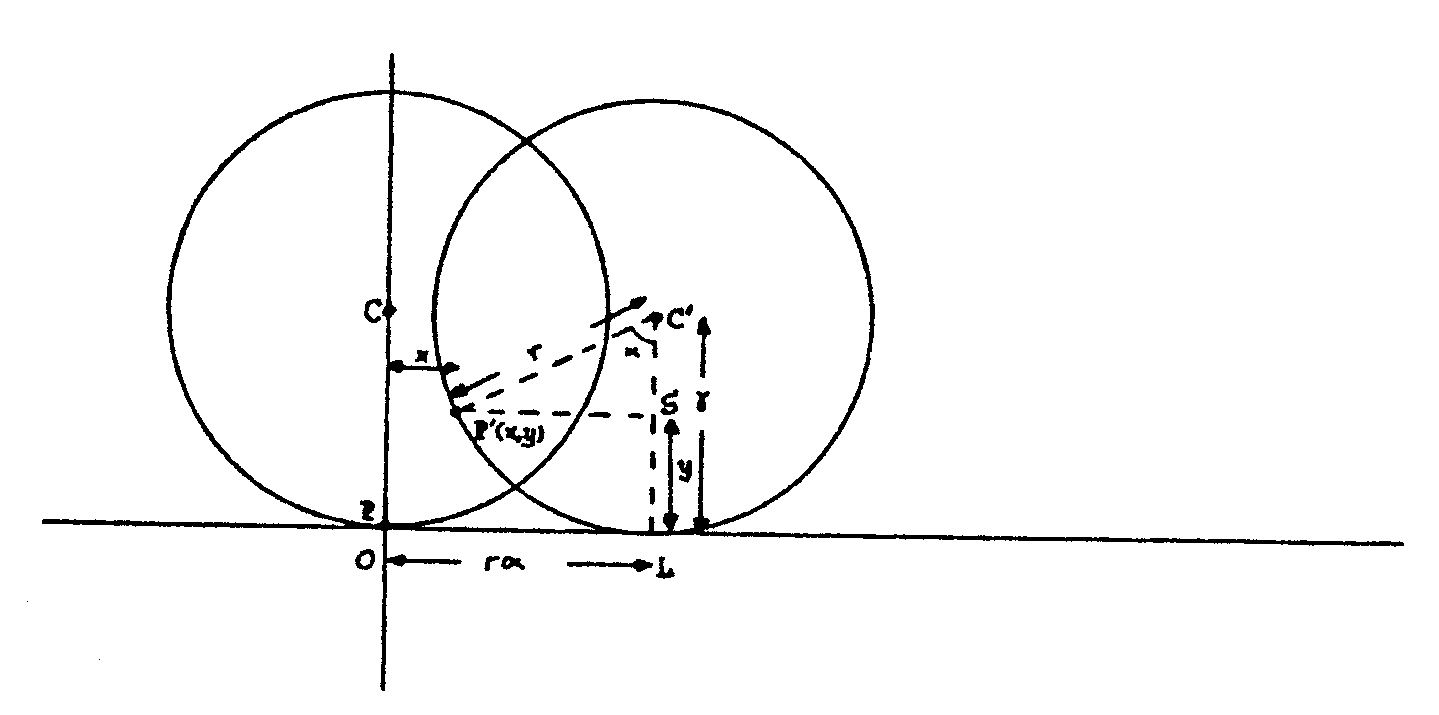
Dejemos que la rueda ruede un poco y veamos dónde va a parar el punto P de la circunferencia. Cuando el centro del círculo C ha pasado a C´, el punto P ha pasado a P´. Este es el punto cuya ecuación queremos. Llamamos a sus coordenadas (x,y). Como la rueda no resbala sobre el suelo, lo que sabemos es que la longitud del arco LP sobre la circunferencia es igual a la longitud del segmento rectilíneo OL. Si llamamos a al ángulo LC´P´ medido en radianes, resulta OL=LP´=ra. Por otra parte, las coordenadas de P´en nuestro sistema son
 
        x = OL - P´S = raa - rsena
        y = SL = C´L - C´S = r - rcosa
 
Así obtenemos la ecuación en coordenadas paramétricas (parámetro a) de la cicloide
 
        x = ra - rsena
        y= r - rcosa
 
Si se intenta eliminar aquí a sale algo más lioso y es preferible dejarlo así.
 
        La cicloide tiene propiedades geométricas muy interesantes. ¿Cuál será su longitud? Fácil
 
dx / da = r(1-cosa); dy / da = rsena.
   
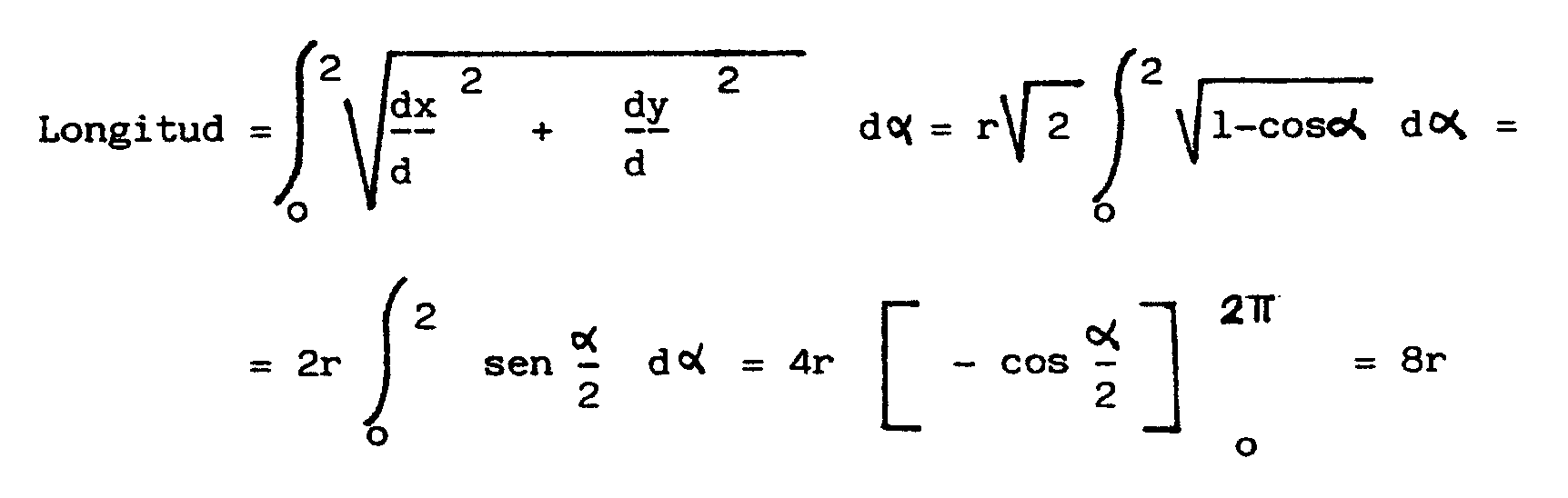
Así resulta que la longitud de la cicloide es 8 veces la del radio de la rueda. No tiene nada que ver con P como uno podría esperar.
 
        La longitud desde el punto 0 hasta el punto correspondiente al valor b del parámetro será
   
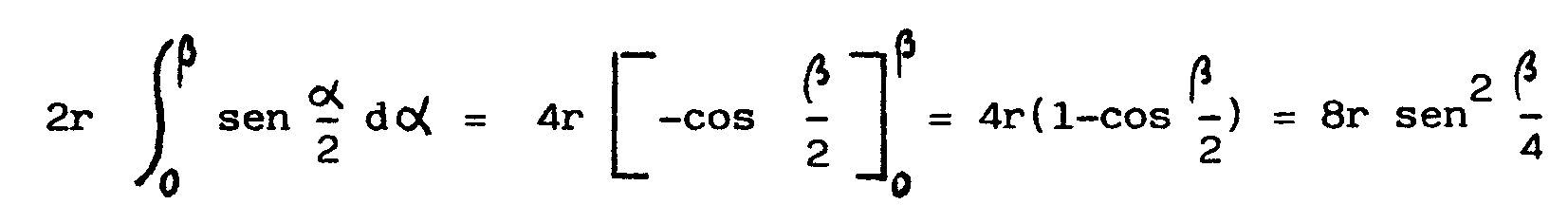
        ¿Cual será el área bajo la cicloide? Se halla de modo sencillo una vez que tenemos la ecuación de la curva:
   
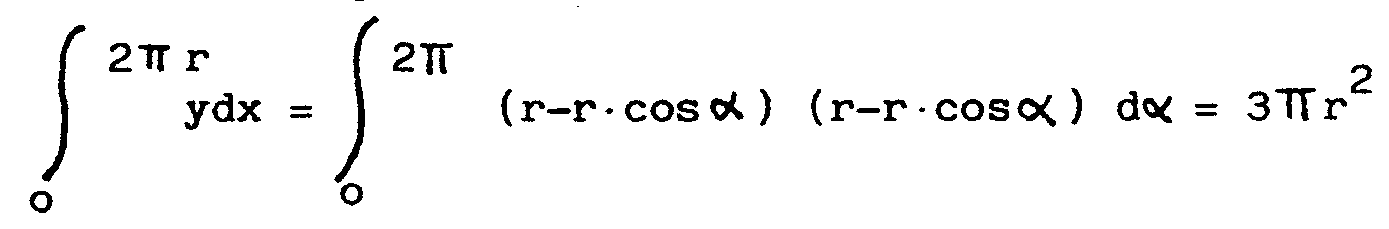
Así el área bajo la cicloide es tres veces la del círculo que engendra la curva. Por tanto las áreas de las tres regiones señaladas en la figura siguiente son iguales.
   
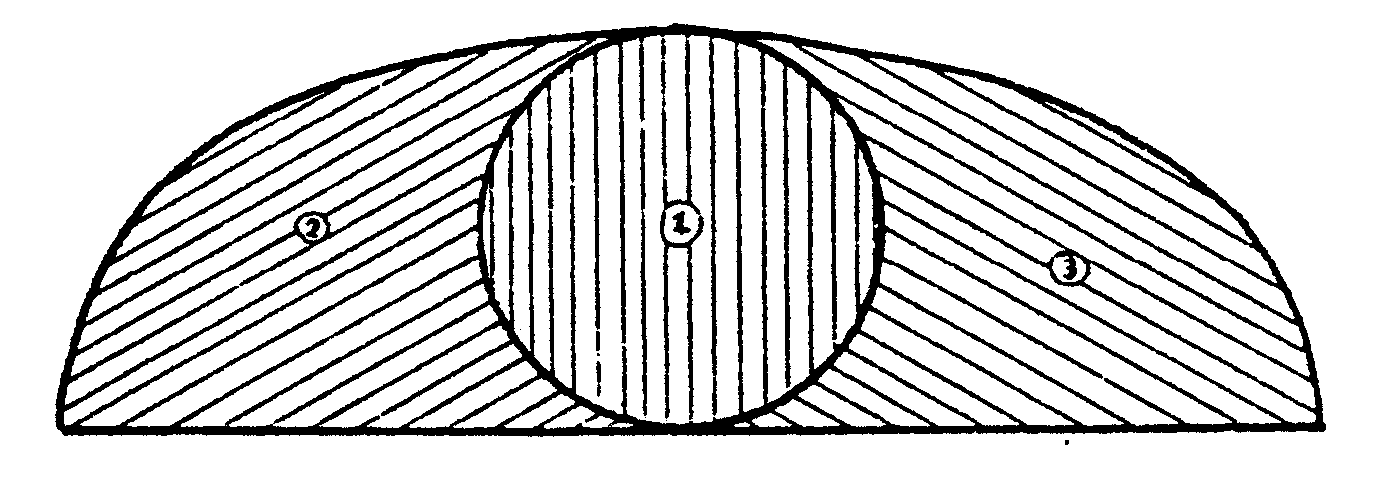
        Vamos a determinar ahora la normal, es decir la perpendicular a la tangente, en un punto (x,y) de la curva correspondiente al parámetro a. Tenemos  
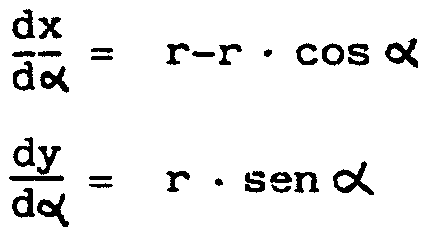
La pendiente de la normal será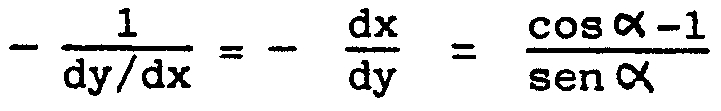 
 
y por tanto la normal en el punto de parámetro a tendrá por ecuación
   
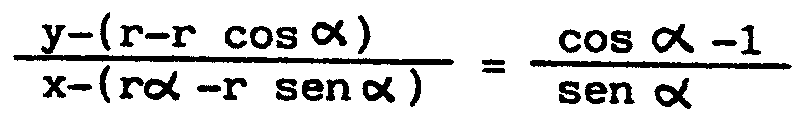
es decir, haciendo operaciones xcosa - ysena - x - racosa + ra = 0  
Ya tenemos la normal en cada punto de la cicloide. Vamos a hallar ahora la envolvente de estas rectas, es decir, la curva que es tangente a todas ellas. ¿Cómo se hace? Sólo hay que derivar la ecuación de las rectas con respecto a a y eliminar a entre la ecuación que resulta y la primera, la de las normales. Así hay que eliminar a entre las dos siguientes xcosa - ysena - x - ra + ra = 0 - xsena - ycosa - rcosa + rasena + r = 0  
En lugar de eliminar a vamos a hacer algo más sencillo, despejar x e y en función de a. Así obtendremos las ecuaciones paramétricas de la envolvente. Como por arte de magia las cuentas salen facilísimas. Se multiplica la primera ecuación por cosa y la segunda por sena, se suman y sale x. De modo análogo para y. Resulta una cosa muy simple. x = ra + rsena y = - r + rcosa  
¿Qué curva es ésta? Si se representa se parece a la cicloide en su forma. ¿Será una cicloide? Vamos a trasladar los ejes al punto (rP, -2r) para comparar con la ecuación de la cicloide, referida al mismo tipo de ejes, que hemos hallado antes. Así resulta la ecuación
 

 
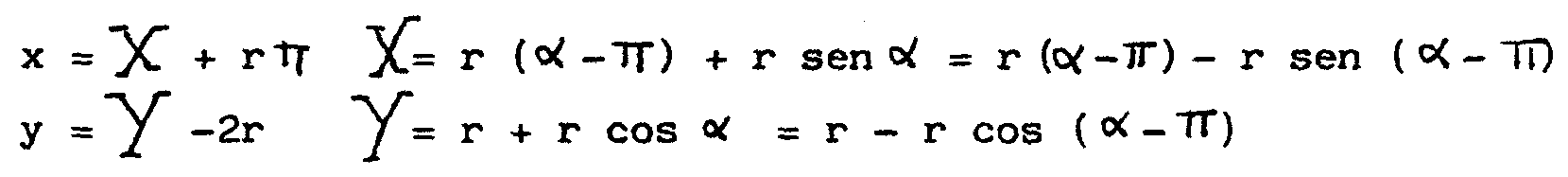
y llamando a - P = q  obtenemos
   
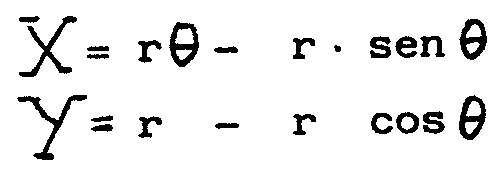
con lo que resulta que... ¡la envolvente de las normales a la cicloide es la misma cicloide trasladada rp a la derecha y 2r hacia abajo! No hay muchas curvas con esta propiedad, como se puede  comprobar mirando las conocidas, circunferencias, elipse...
   
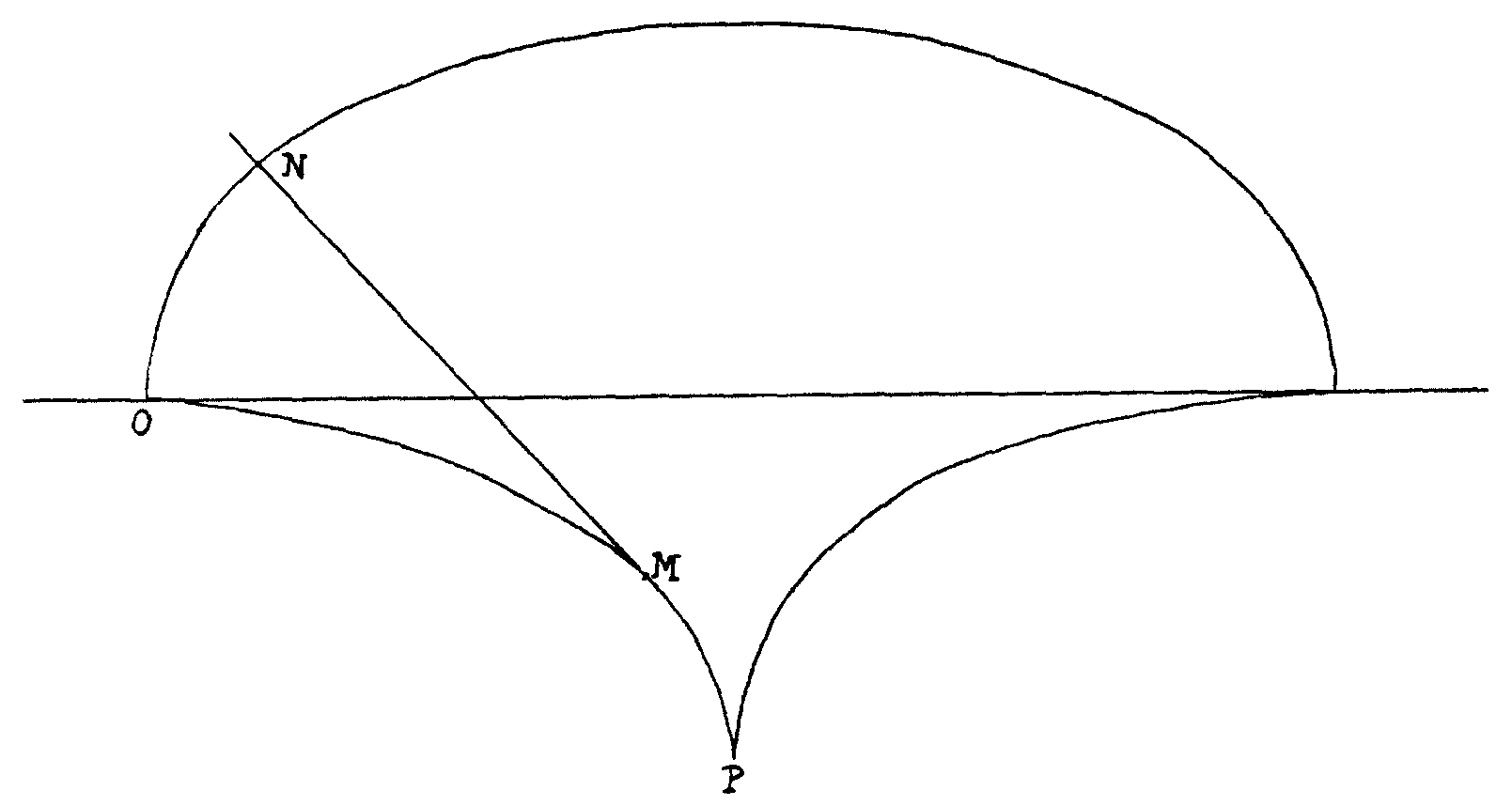
        Vamos a seguir echando algunas cuentas más. Tenemos la ecuación de la cicloide
   
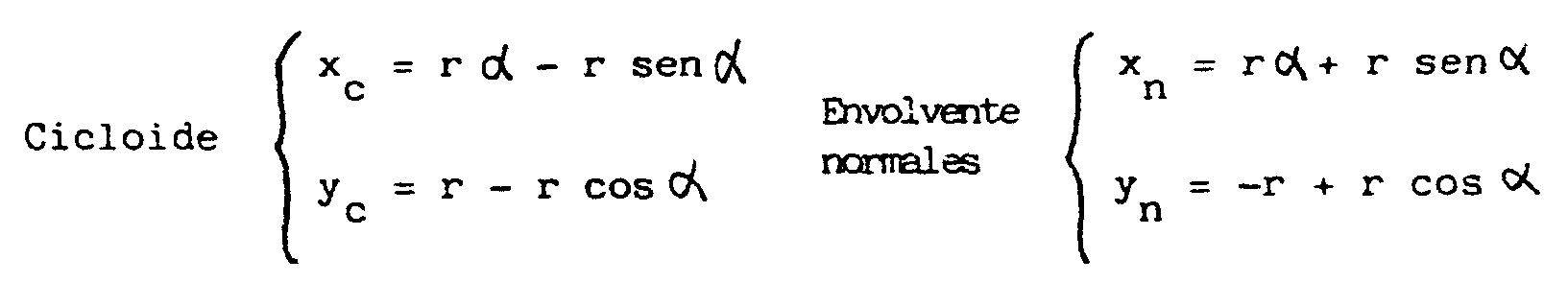
y la de la envolvente de las normales. Al punto de parámetro sobre la cicloide le corresponde la normal MN que es tangente a la envolvente en el punto M. Conocemos las coordenadas de estos puntos
 
N (ra - rsena, r - rcosa);  M(ra + rsena, rcosa - r)
 
la distancia entre ellos en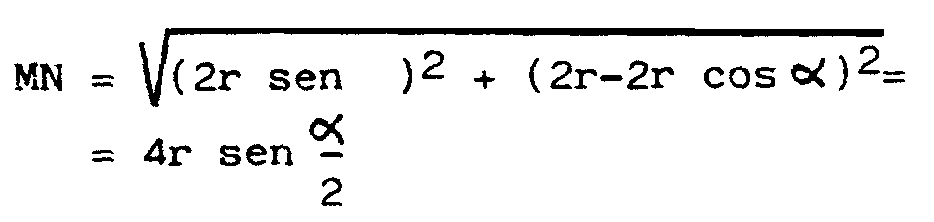 
 
la longitud del arco MP se calcula fácilmente, observando que el punto M corresponde al parámetro a y el P al parámetro p. Así
 

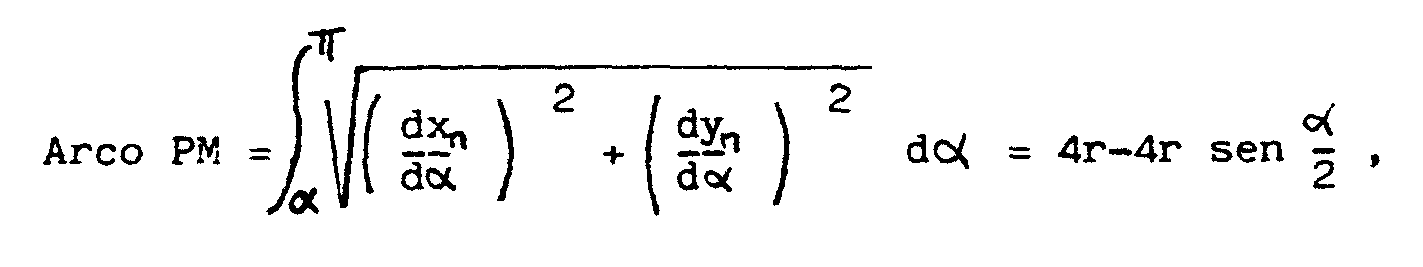
  MN + Arco PM = 4r  
De todo esto resulta un hecho geométrico interesante y que tendrá aplicaciones como veremos despueés en la construcción de relojes de péndulo. Resulta por nuestras cuentas que: MN + arco MP sobre la cicloide = constante = 4r. Así, si sobre el borde de la cicloide OP fijas un cordel y vas desplazando el extremo en  O manteniéndolo tirante para que la parte suelta siga siendo tangente a la cicloide OP, entonces resulta que este extremo que se desplaza describe la cicloide de arriba ON.
 
        Si las propiedades geométricas de la cicloide son interesantes, sus propiedades físicas lo son aún más.
 
        Haciendo girar la cicloide invertida alrededor de su eje de simetría, se forma un cuenco como este
   
y como vimos en el apartado: una curva polivalente, si desde dos puntos a altura distinta del cuenco se dejan caer al mismo tiempo dos canicas, resulta que llegan al punto más bajo del cuenco simultaneamente.
 
        Con un poco de física podremos llegar a este resultado interesante. Nuestra cicloide invertida tiene por ecuación
    x = ra - rsena y = rcosa - r    
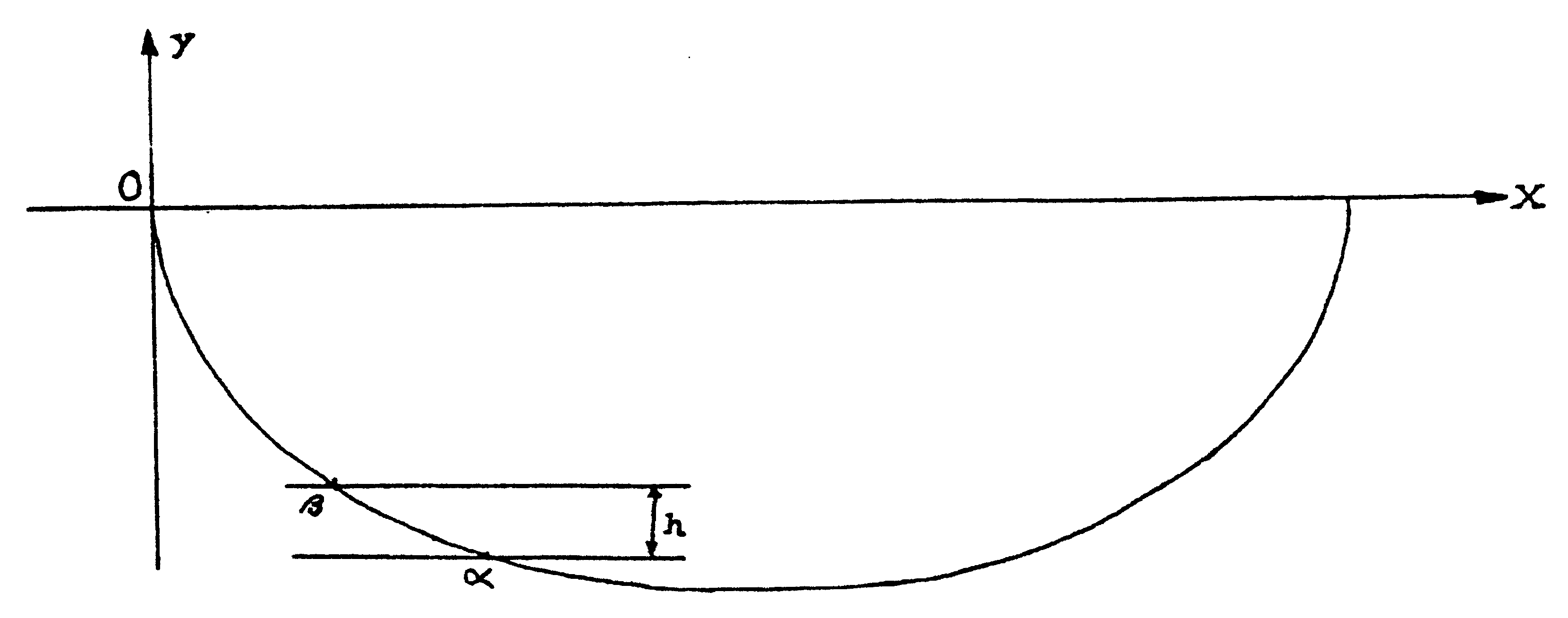
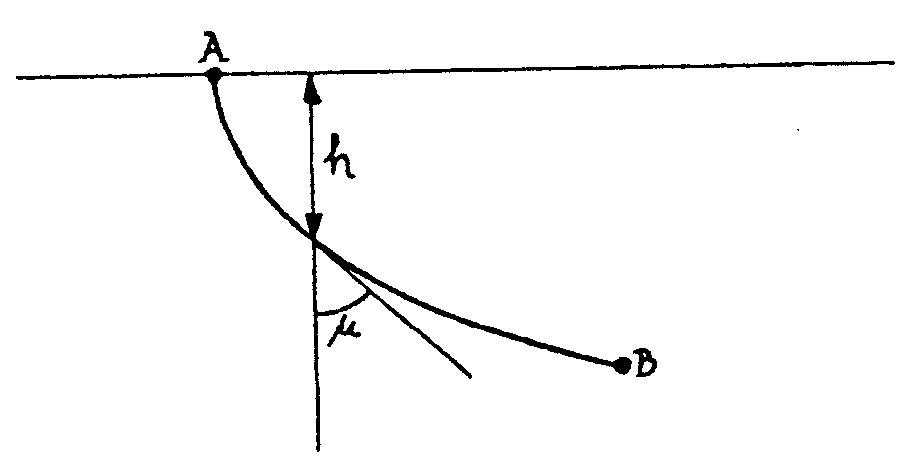
Si se deja caer una bola desde el punto del parámetro b, entonces, según la ley de caída libre, llega al punto de parámetro a con una velocidad   , siendo h la diferencia de altura entre los dos puntos, es decir
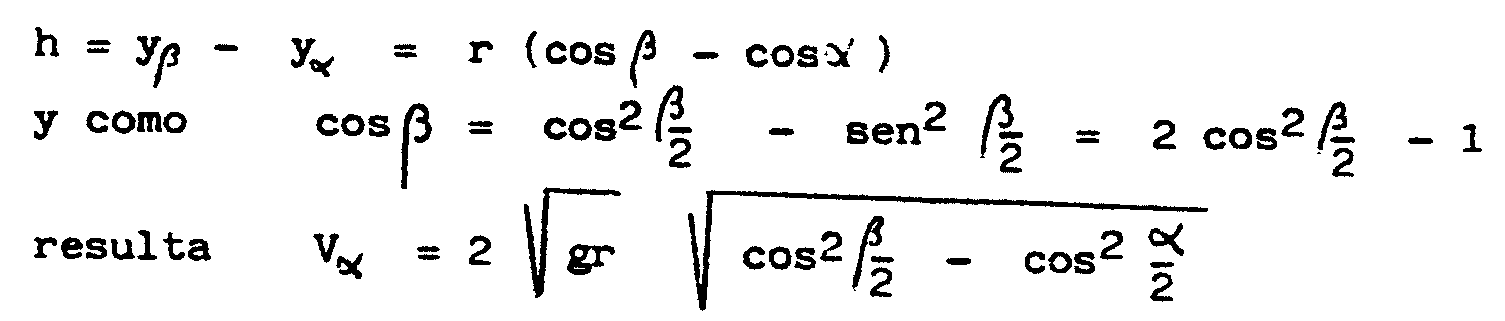    El elemento de longitud de la curva en a es
 

 
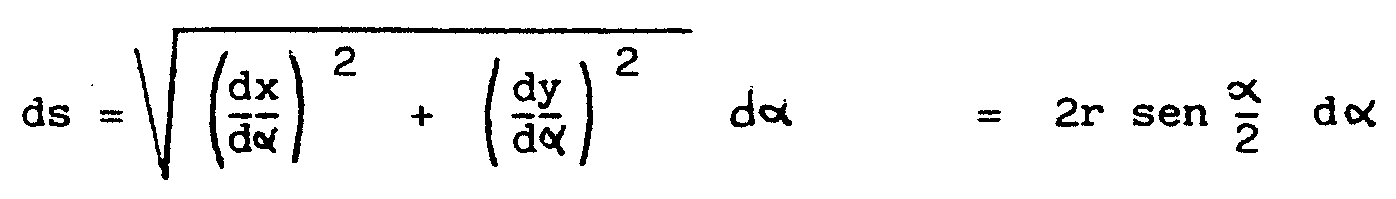
Como sabemos, espacio = velocidad x tiempo, y así podemos escribir
 

 
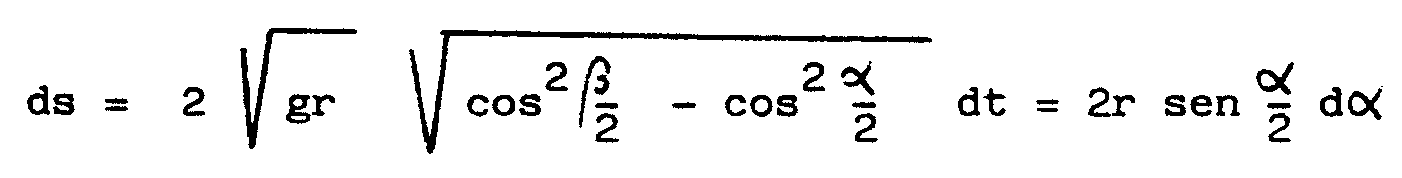
con esto resulta
 

 
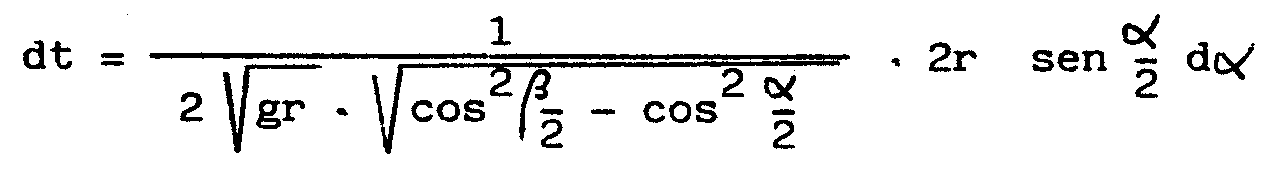
        Por tanto, el tiempo que tarda en la caída por la cicloide desde el punto de parámetro b al punto más bajo del cuenco, de parámetro p, será
 

 
 
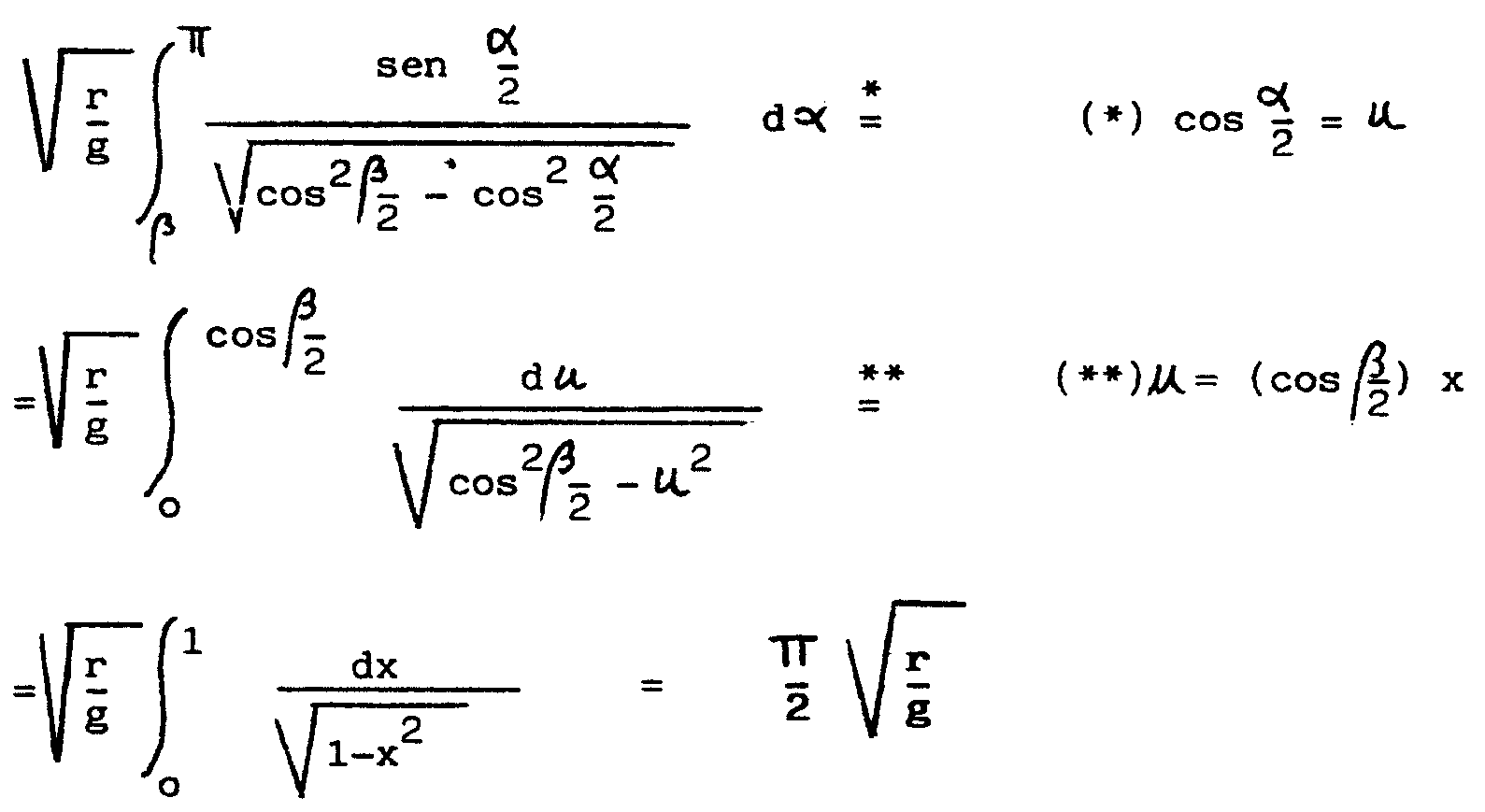
  QUE ES INDEPENDIENTE DE b           Huygens fue el primero en descubrir esta propiedad en 1673 y en darle una aplicación práctica. Huygens había estudiado a fondo los relojes de péndulo y observó que cuando un reloj tiene una variación en la amplitud de la oscilación del péndulo, entonces deja de ocntar el tiempo correctamente. ¡Pero si la lenteja del péndulo se moviese no en una circunferencia, como en el péndulo normal, sino a lo largo de una cicloide, entonces aunque la amplitud de oscilación fuera mayor o menor, el período del péndulo seguiría siendo el mismo, como hemos visto por nuestras cuentas!
 
        ¿Cómo lograr que la lenteja del péndulo se mueva describiendo una cicloide? Huygens se las ingenió mediante una de las propiedades geométricas de la cicloide que hemos visto antes. Si miramos la figura siguiente, podemos apreciar que es como la de la página 48 sólo que invertida
   
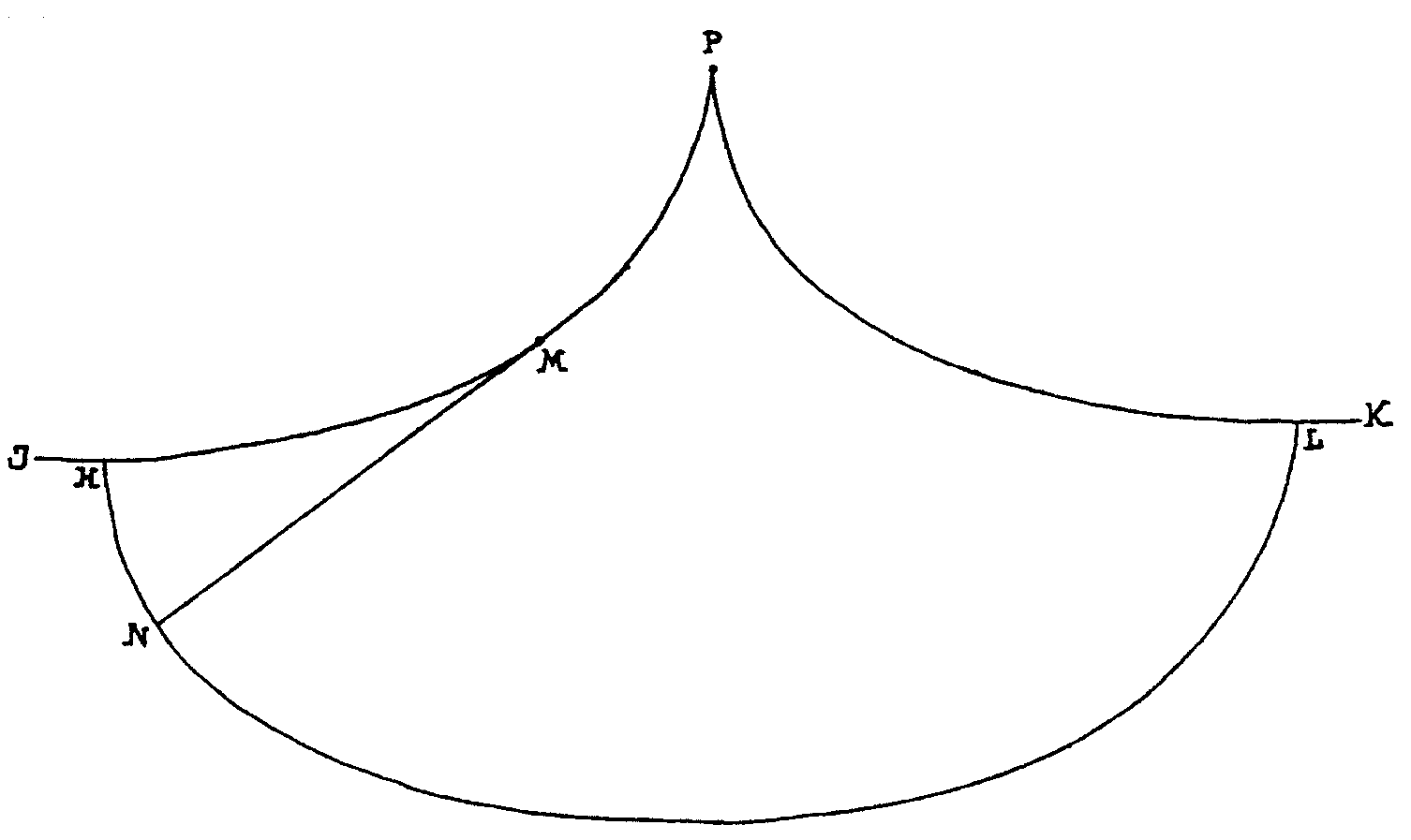
Si cuelgas el péndulo de P con una cuerda de longitud 4r y colocas a ambos lados de P una cicloide PHJ y PLK como topes, según está indicado, entonces se sabe que N describe una cicloide igual. ¡Sea cual sea la amplitud del movimiento pendular de N, el período es el mismo! Es un péndulo que se compensa solo... (ver el apartado: Una curva polivalente).
 
        La cicloide tiene otra propiedad física más importante aún en la historia del desarrollo de las ideas matemáticas.
 
        En 1969 Johann Bernoulli propuso un reto a todos los matemáticos de Europa. Consistía en el siguiente problema: te fijan dos puntos A y B en un plano vertical. A más alto que B pero no en la misma línea vertical. Te dan un alambre y una cuenta que se puede ensartar en él. Te piden que encuentres qué forma de curva debes dar al alambre uniendo A con B de modo que la cuenta ensartada emplee el menor tiempo posible en bajar desde A hasta B.
   
        Fueron unos cuantos los matemáticos que resolvieron el problema en el plazo establecido, entre ellos Newton, Huygens, Leibniz, Jakob Bernoulli(hermano de Johann).. Este último dio una solución mediante un método originalísimo que dio lugar a toda una rama de la matemática moderna, el cálculo de variaciones.
 
        La solución, como ya vimos en el apartado anteriormente mencionado, es la cicloide. Una cicloide que pase por A y B que salga vertical de A, como se indica en la figura
   
        La solución de Jakob Bernoulli fue un poco complicada. La de Johann Bernoulli, una mezcla de física y geometría, fue genial, pero no tan fecunda y general como la de su hermano. Veamos un esquema de la de Johan en unos cuantos puntos.
 
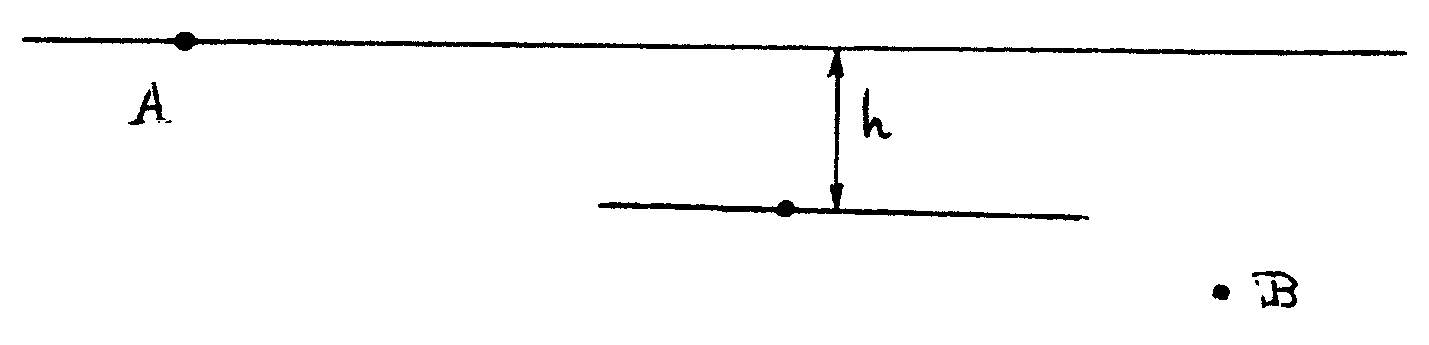
        (1) Baje por donde baje la cuenta
cuando haya bajado h su velocidad será 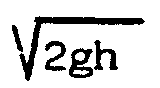 (ley de caída libre). Lo que no sabemos aún es qué dirección tendrá esta velocidad.
   
        (2) Sabemos (principio de Fermat) que la luz viaja de un punto a otro en el mínimo tiempo posible.
 
        (3) Sabemos también que la luz tiene una velocidad distinta según el medio en el que viaje. Precisamente ésta es la razón del fenómeno de la refracción. Si tenemos dos medios distintos y la luz viaja a velocidades V1, V2 en ellos, entonces, la ley de refracción nos dice que
 

   
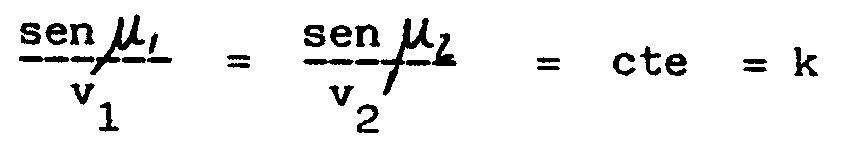
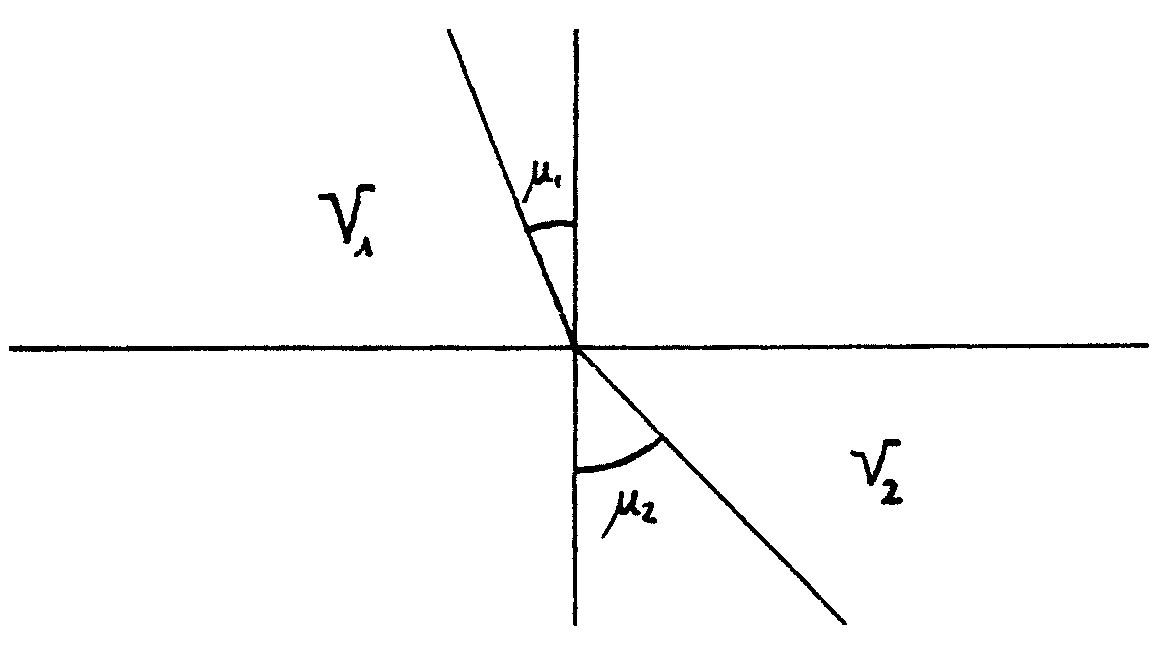
        (4) Imaginemos un medio óptico formado por láminas l1, l2, l3,...ln, horizontales y delgadas, tal que la velocidad de la luz en cada una de ellas es v1, v2, v3..., como se indica en la figura. Entonces un rayo que parta de A y llegue hasta B seguirá una trayectoria como se indica, de modo que
 

   
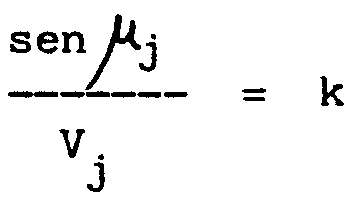
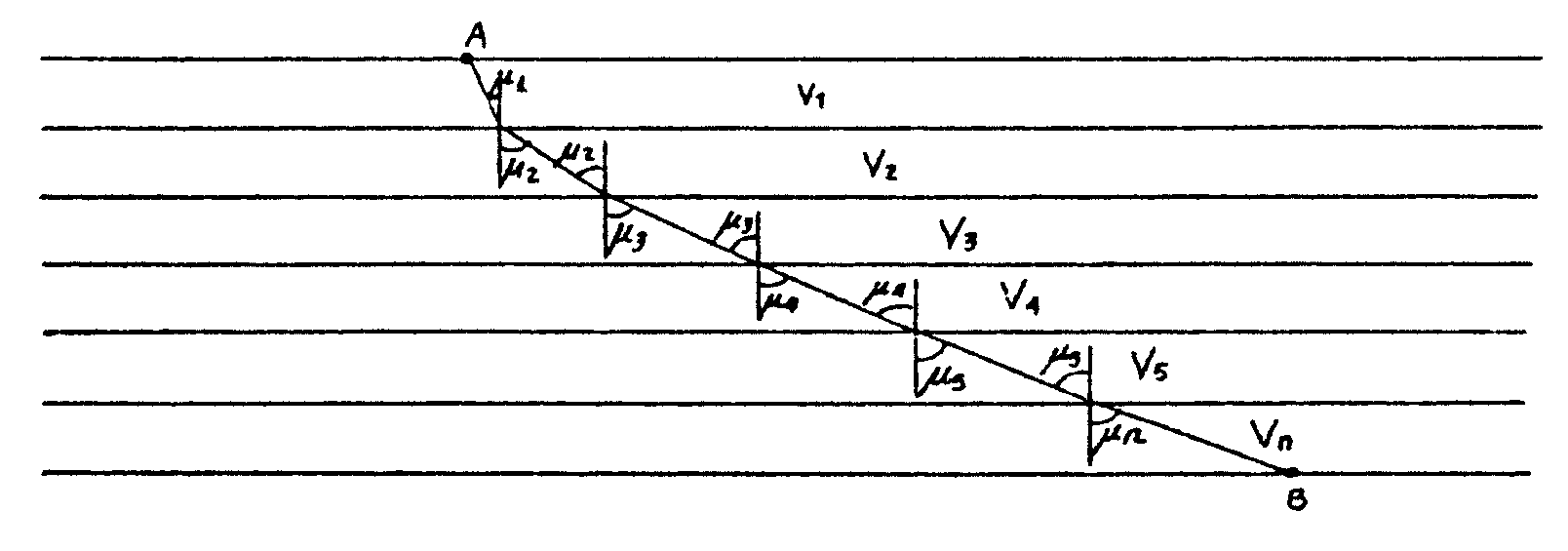
¡ Y ESE CAMINO DEL RAYO DE LUZ SERIA EL CAMINO DE TIEMPO MINIMO PARA IR DE A A B CON LAS VELOCIDADES INDICADAS!
 
        (5) En el caso de nuestro problema, sabemos que la velocidad al descender h es precisa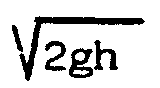mente . Así, el camino que da el mínimo tiempo será el camino que sigue un rayo de luz en un medio tal que la velocidad de la luz varíe continuamente al descender h y sea precisamente 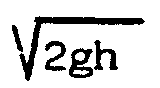. Pero para este camino ya sabemos que se verificará
 

   
 
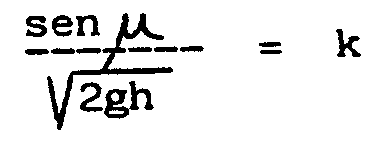
siendo m el ángulo que forma dicho camino con la vertical.
 
        (6) Así la curva que da el camino de tiempo mínimo compatible con la velocidad señalada a cada altura, v = 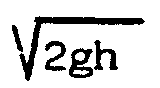, es la que satisface
 

 
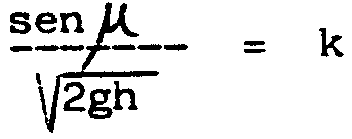
        (7) Vamos a ver que la cicloide es la curva que satisface esta condición
   
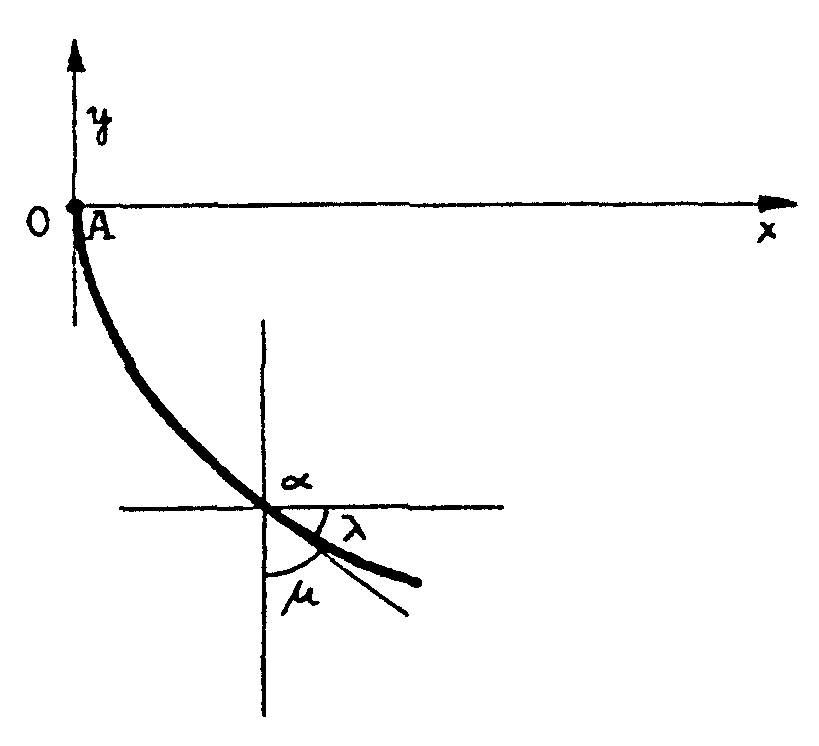
La ecuación es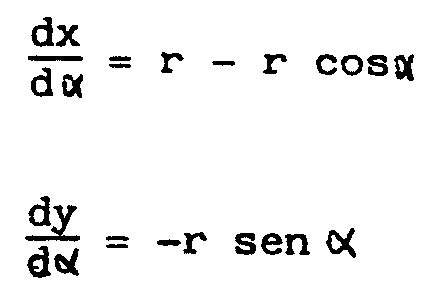 
 
Podemos escribir
 

 
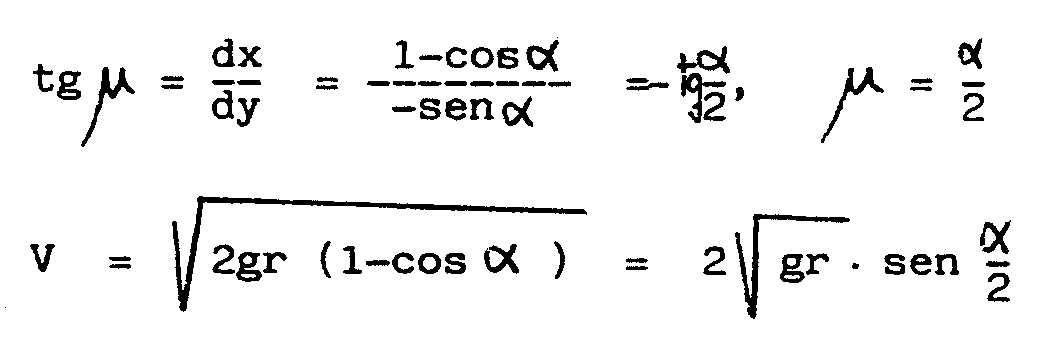
Así, efectivamente,
 

 
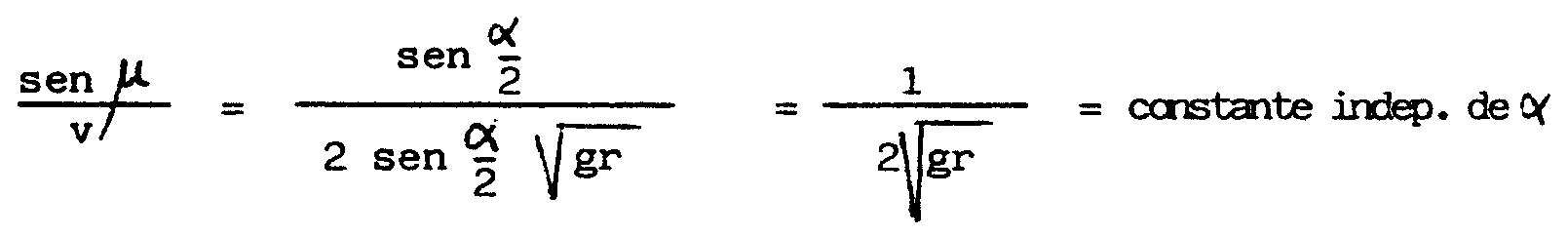
y, por tanto, la cicloide tiene la propiedad que buscamos.