A P E N D I C E S
UN BILLAR MÁS COMPLICADO
Supongamos ahora
que estamos jugando en un billar en forma de triángulo con sus tres
ángulos agudos y que nuestro problema consiste en lo siguiente:
nos dan un punto M de BC. Se trata de elegir una dirección de tiro
de modo que la bola lanzada desde M vaya hacia la banda AC, rebote allí
y luego rebote en la banda AB de modo que vaya a dar al mismo punto M de
salida.
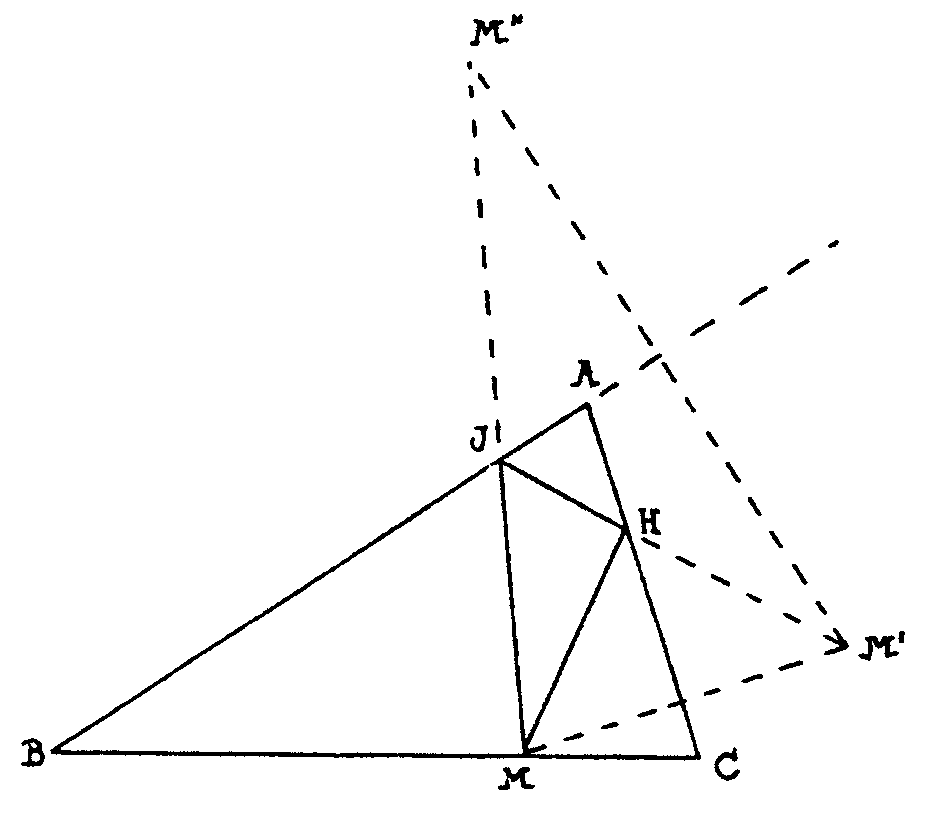
Tenemos la receta del billar normal que nos va a servir
también ahora. Al rebotar en AC sale la bola como si viniera desde
M´, simétrico de M respecto de AC. Al rebotar en AB sale la
bola como si viniera desde M´´, simétrico de M´,
respecto de AC. Como queremos que pase por M, unimos M´´ con
M y esto nos da la última parte de la trayectoria. Unimos luego
J con M´ y obtenemos la otra parte JH y luego MH. Está claro
que, como antes, para que haya solución J debe quedar sobre el segmento
AB y H sobre el segmento AC, lo cual no sucede en un triángulo cualquiera,
pero sí si el triángulo es acutángulo, como hemos
supuesto. Trata de demostrarlo. Es fácil.
Verás
ahora cómo el saber jugar con esta técnica al billar resuelve
un problema curioso e importante. Te dan en el lado AB del triángulo
acutángulo ABC un punto P y en AC otro punto Q. Te piden que determines
el triángulo que tiene por vértices P, Q y el tercero M que
has de fijar tú de tal modo que esté sobre BC y que el perímetro
de MPQ sea mínimo. Piensa
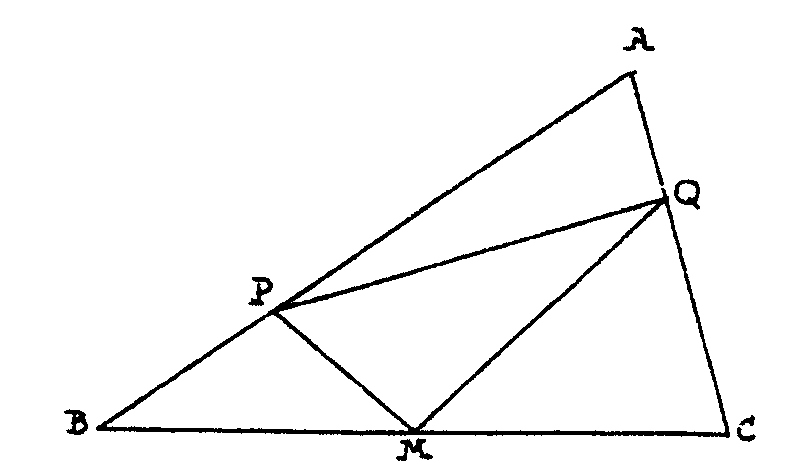
Ha de ser mínimo PQ+PM+MQ. Pero como PQ es fijo,
pues los dos puntos P y Q te los han señalado, resulta que ha de
ser mínimo PM+MQ. Pero esto es algo que ya hemos aprendido antes:
la bola de billar que lanzada desde P a la banda BC vaya a parar a Q es
la que da la trayectoria más corta tocando la banda. Así
tenemos resuelto el problema.
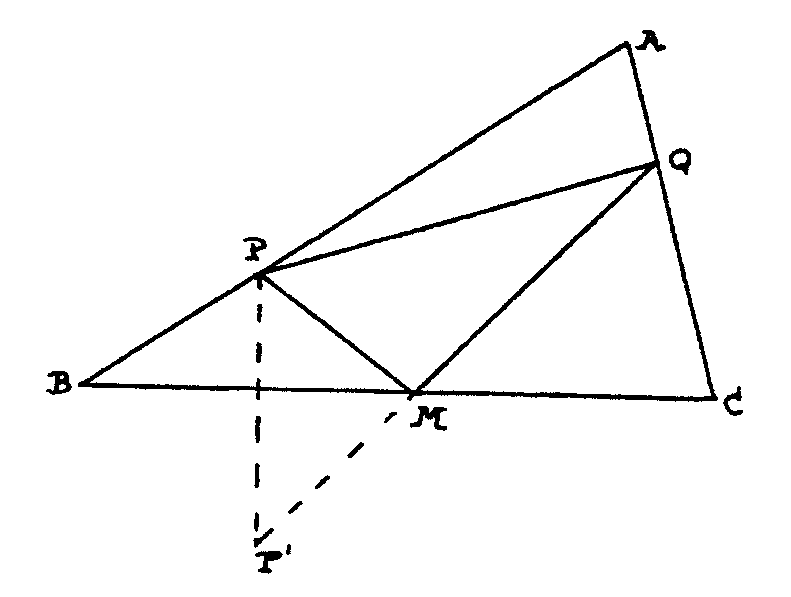
Unimos Q al P´, simétrico de P respecto
de BC y hallamos M.
Vamos un poco
más allá con otro problema parecido. Ahora te dan el triángulo
ABC y no te fijan los dos puntos P y Q, sino sólo P sobre AB. Te
piden encontrar un triángulo MPQ con M sobre BC y Q sobre AC con
perímetro mínimo.
Por lo que
ya sabemos parece natural pensar que si hay una trayectoria de bola de
billar que salga de P, vaya a M en BC, rebote allí y vaya a Q en
la banda AC y vuelva a P, esta trayectoria PMQP dará el triángulo
de área mínima. Ya tenemos una conjetura que parece buena,
por nuestras experiencias anteriores. Esta trayectoria existe y ya sabemos
trazarla en un triángulo acutángulo como el que nos han dado.
Trazamos el punto P´, simétrico del P respecto de BC, luego
el P´´, simétrico del P´ respecto de AC, etc...
Obtenemos así el triángulo PMQ. ¿Será éste
de verdad el de perímetro mínimo que buscamos? Para verlo
lo compararemos con otro cualquiera PM*Q*. Observa la figura siguiente:
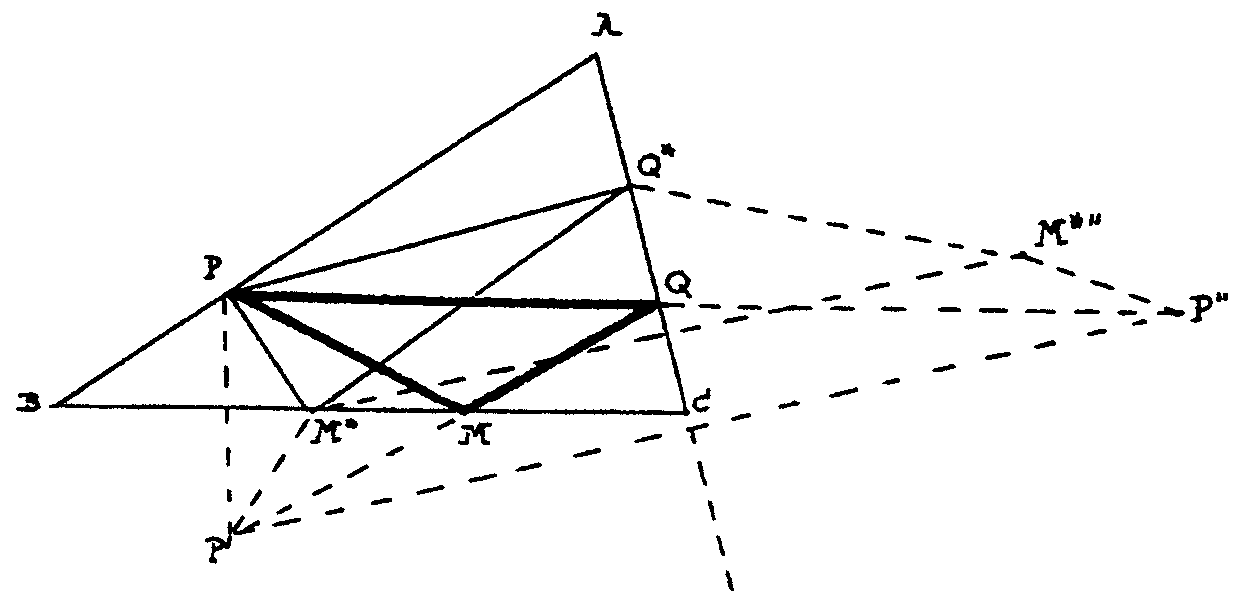
Ahí tienes que PM=MP´=M´´P´´.
Asímismo, MQ=M´´Q. Así el perímetro de
PMQ es igual al segmento PP´´. ¿Y el perímetro
de PM*Q*? Fíjate que M* tiene su simétrico M*´´
respecto de AC fuera de PP´´. Así el perímetro
de PM*Q* es
PM* + M*Q* + Q*P = P´´M*´´
+ Q*M*´´ + Q*P
y esto último es la longitud de una quebrada de
extremos P y P´´. Así este perímetro es claramente
mayor que PP´´ que era la longitud del perímetro de
PMQ.
Para rematar
este tipo de problemas imagínate que ahora no te fijas más
que el triángulo ABC y te piden que determines un triángulo
MPQ con M en BC, P en AB y Q en AC que tenga perímetro mínimo.
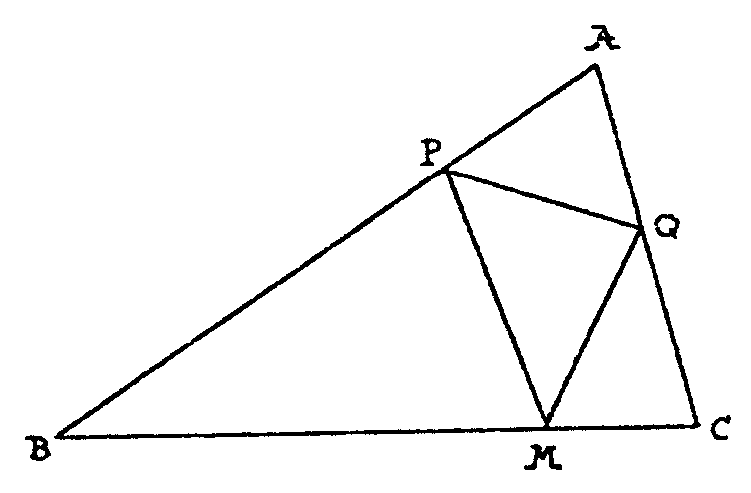
Parece claro,
con la experiencia acumulada que tenemos, que si hay algún triángulo
MPQ tal que lanzando la bola desde P en dirección a M ésta
rebote hacia Q y allí rebote hacia P y al mismo tiempo que esta
propiedad se verifique para P y para Q, es decir que lanzando P hacia M
rebote hacia Q..., entonces este triángulo debería ser el
de perímetro mínimo.
Así tenemos dos preguntas que contestaremos. ¿Existirá
tal triángulo maravilloso? Y si existe ¿tendrá de
verdad la propiedad de mínimo perímetro? Es curioso. El triangulo
MPQ con la propiedad que buscamos no sólo existe sino que además
es un viejo conocido. Es el triángulo de los pies de las alturas
HaHbHc,
que se suele llamar el triángulo órtico. Para ver esto, observa
primero que BHcHHa
es un cuadrilátero que se puede inscribir en una circunferencia
de diámetro BH (recuerda que H es el punto de intersección
de las tres alturas, el ortocentro), ya que HHaB
es un ángulo recto y HHcB también.
Así
los ángulos HHaHc y HBHc
que están inscritos en el mismo arco, son iguales. Fíjate
además en que HBHc = 90-A pues el
triángulo ABHb es recto en Hb.
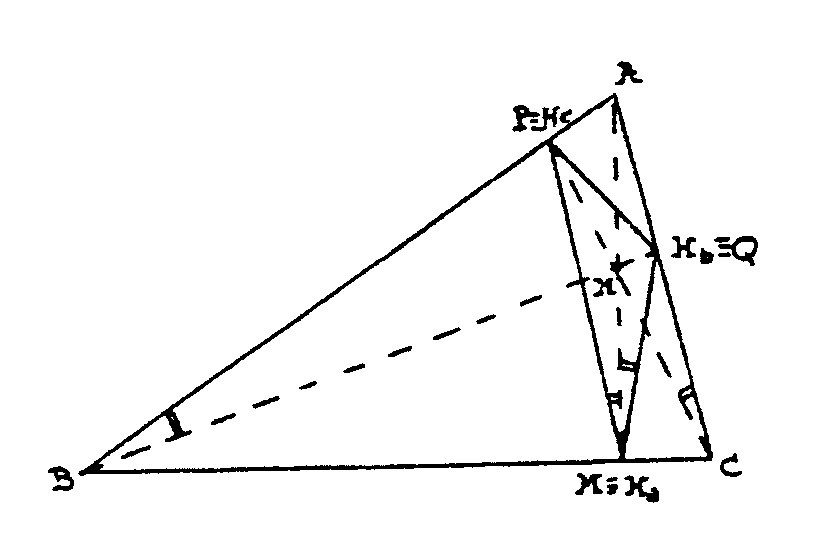
Asímismo el cuadrilátero HHbCHa
se puede inscribir en una circunferencia de diámetro CH y del mismo
modo que antes HHaHb=HCHb=90-A.
Así AHa es bisectriz de HcHaHb.
Si desde Hc se lanza una bola hacia Ha
ésta rebota hacia Hb. Con cuentas
iguales se demuestra que esta bola rebota en Hb
hacia Hc y en Hc
hacia Ha. Así éste es el
triángulo MPQ que estábamos buscando con la propiedad de
que si desde cada vértice se lanza una bola a otro, ésta
rebota en las dos bandas y vuelve al punto de partida.
Queda por
ver si es el de perímetro mínimo. Pero esto resulta sencillo
comparando con cualquier otro como hicimos en el problema anterior. Observa
la figura siguiente en la que M1
es simétrico de M respecto de AB, M2
es simétrico de M respecto de AC y análogamente M*1
es simétrico de M* respecto de AB y M*2
es simétrico de M respecto de AC. El ángulo M1AM2
así como el M*1AM*2
miden 2A y así se pueden escribir las cuentas siguientes con las
que queda demostrado que el perímetro de MPQ es menor que el de
M*P*Q*
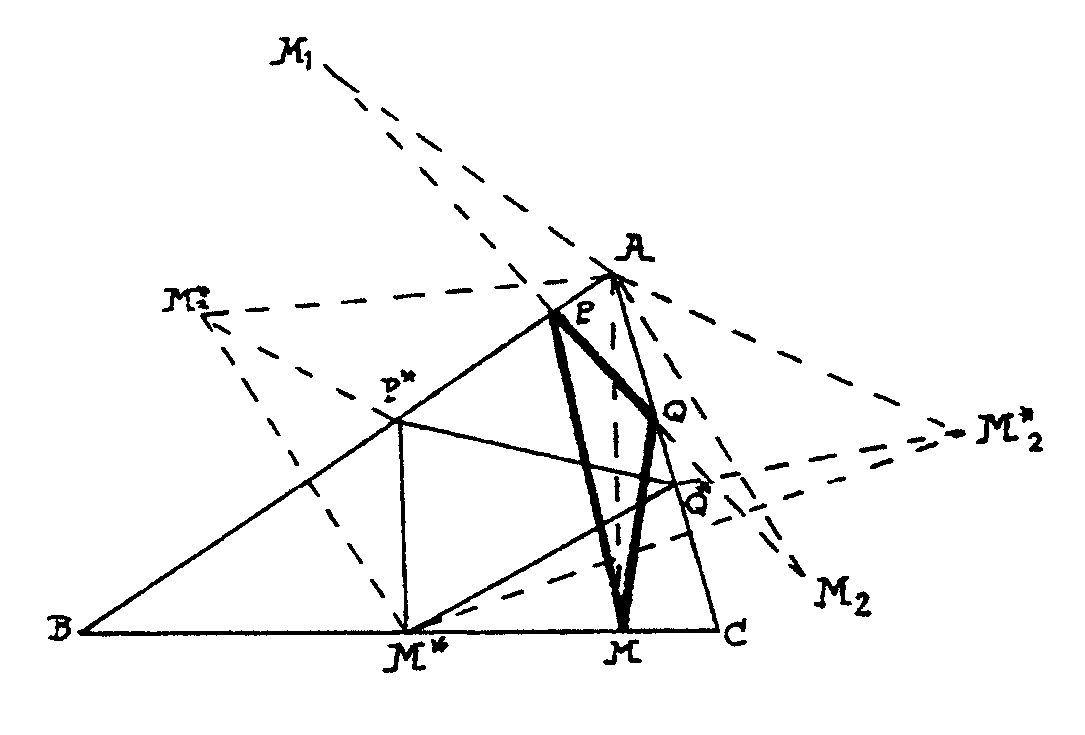
PQ+PM+QM = M1M2
= 2AM1 senA = 2AM
senA
P*Q*+P*M*+Q*M*=P*Q*+P*M*1+Q*M*2>M*1M*2=2AM*senA>2AMsenA










