LA TIRA DE GEOMETRÍA
EN LA TIRA DE PAPEL.
Hazte, si puedes,
con un buen trozo de esos rollos de papel que se emplean en las máquinas
registradoras de cobrar dinero. O si no, hazte tú mismo una tira
de papel larga, como de 4cm. de anchura, pegando tiras cortadas de una
hoja de papel. Procúrate unas tijeras y papel celo. Porque vamos
a hacer la tira de geometría con tu tira de papel.
Para empezar,
piensa un poco. ¿Cómo te harías un cuadrado con tu
tira solamente plegando?... Fácil, ¿no?
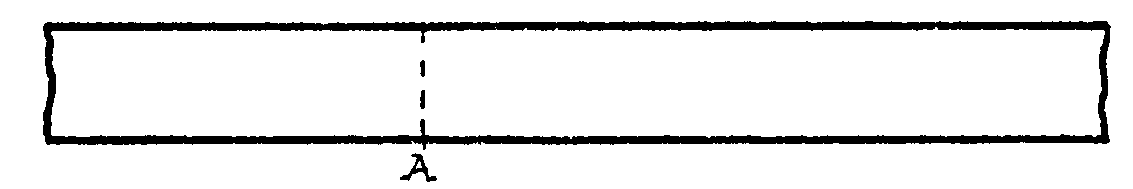
Pliega por A y así resulta un pliegue perpendicular.
Queda del modo siguiente
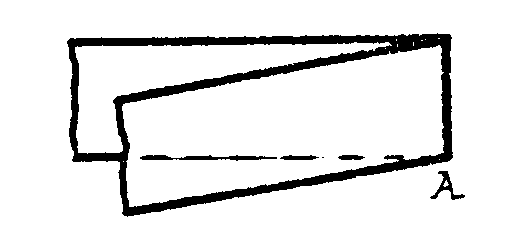
Al desplegar resulta marcado el pliegue perpendicular
Pliega ahora así
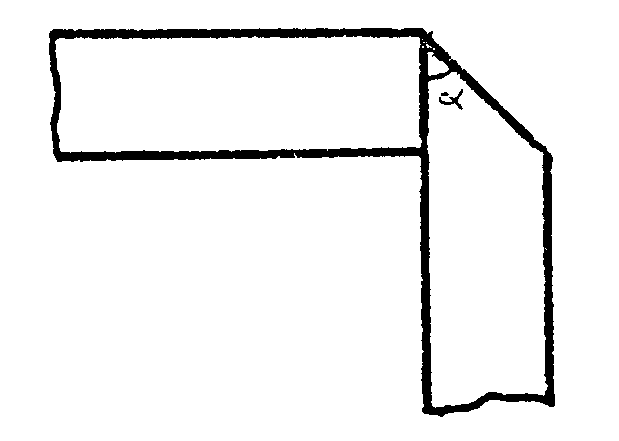 Observa que el ángulo es de 45º
Observa que el ángulo es de 45º
Despliega y observa que tienes estos pliegues

Ahora ya está claro. Pliegas así
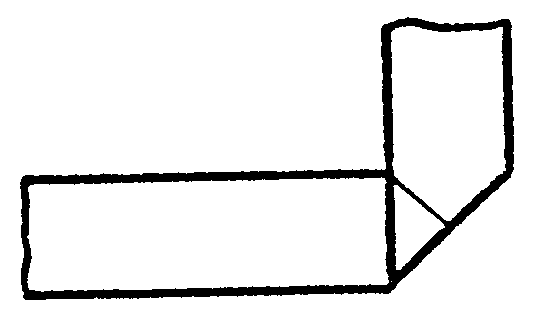
Y al desplegar tienes esto
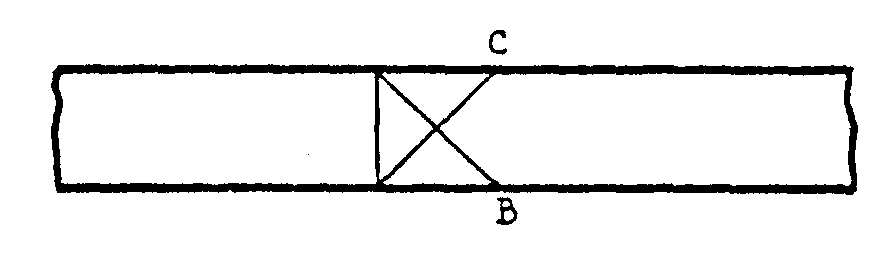 Pliegas por los puntos B y C y te resulta el cuadrado.
Pliegas por los puntos B y C y te resulta el cuadrado.
Ahora piensa otra vez. ¿Cómo hacerte con
un triángulo equilátero? Seguro que se te ocurre, pues ya
sabes cómo dividir un ángulo en tres partes iguales plegando
el papel. Tanteando un poco puedes formar primero un cucurucho y luego
dos pliegues con los que la tira te va a quedar así
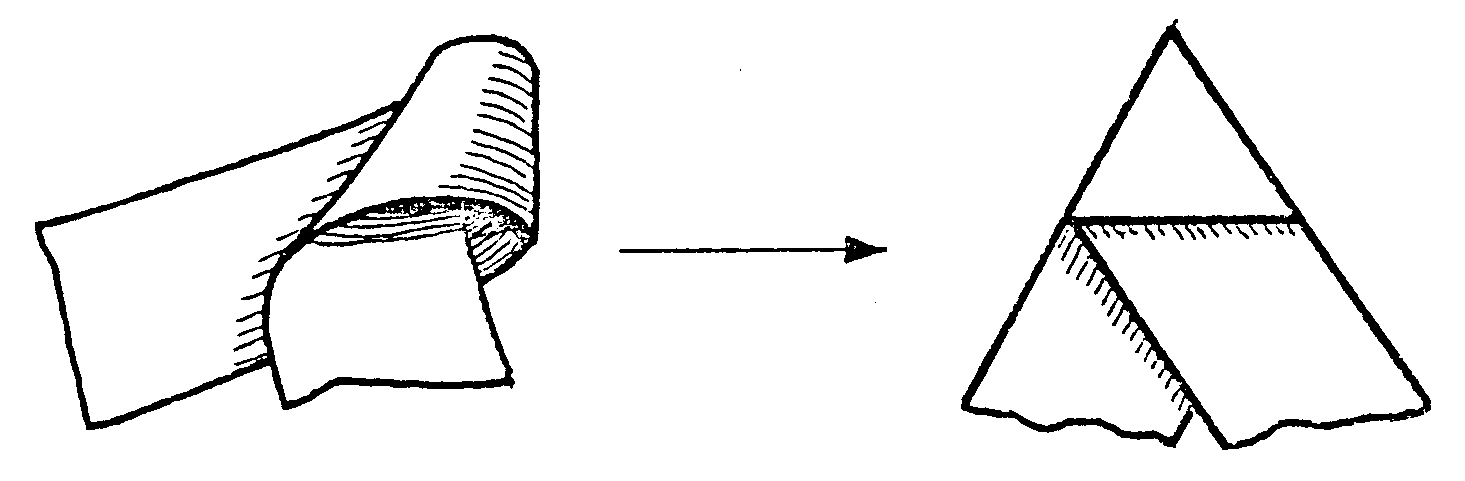
Observa que en la tira plegada hay dos pliegues que determinan
(por coincidir tres ángulos iguales alrededor del vértice).
Al desplegar queda la cosa así
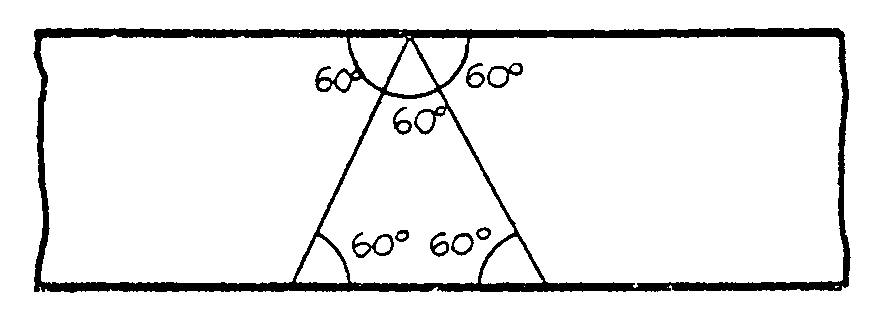
y por la igualdad de ángulos determinados por
paralelas, resulta que los ángulos señalados por los pliegues
en la parte baja de la tira son también de 60º. Así
obtienes un triángulo equilátero.
Ya tienes
el cuadrado, el triángulo equilátero... ¿más
polígonos regulares? El exágono es fácil, una vez
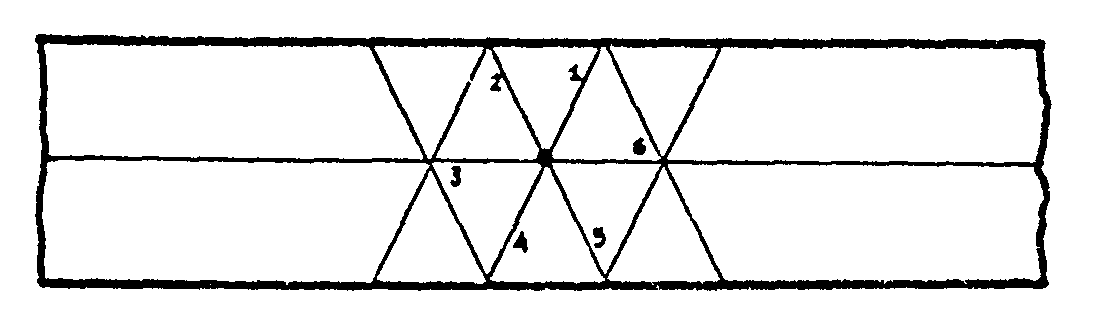
que tienes el triángulo equilátero. Tienes la tira así

Doblas por la mitad y te resulta así

Ahora pliegas unas cuantas veces por los pliegues que
han quedado señalados de antes y verás cómo al desplegar
te resulta el exágono con los radios y el centro señalados
de esta forma
Vamos a seguir
con nuestra colección de polígonos regulares. A por el pentágono.
Este es un poco más rebuscado. ¿Se podrá hacer con
la tira? ¿Qué más podemos hacer con la tira? Piensa,
piensa... Después de mucho pensar, es posible que no se te ocurra
nada más que hacerte una corbata con la tira y... ¡mira por
dónde! ésa es la pista para el pentágono regular.
Haz un nudo con la tira, sólo plegando, sin arrugarla, primero así
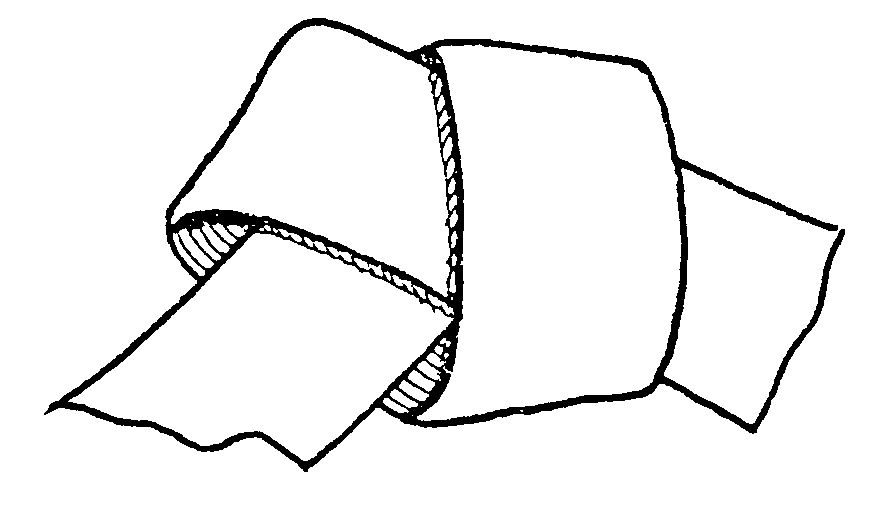
y luego plegando con cuidado hasta que quede del siguiente
modo
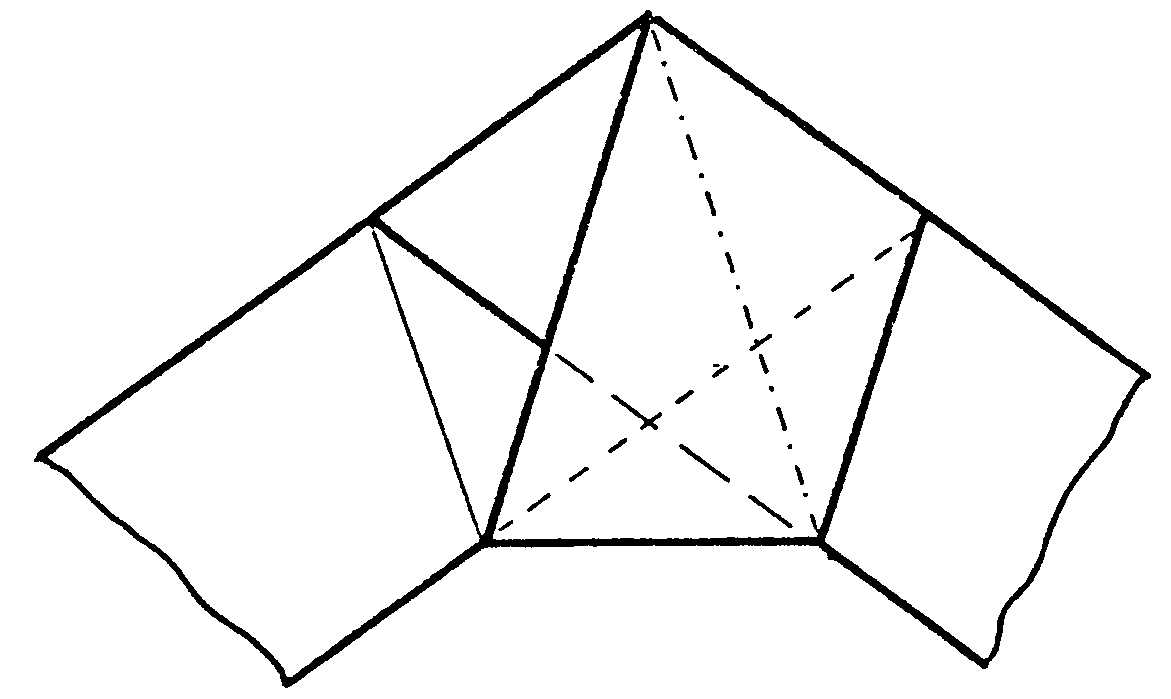
En puntos van las partes del borde de la tira que no
se ven. Ahí tienes el pentágono regular, recortando la tira
y pintando sólo los bordes.

¿Sabrías demostrar que efectivamente todos
sus lados y todos sus ángulos son iguales? Aquí tienes un
esquema de la demostración, pero si te aburre déjalo para
otro momento y pasa adelante.
Esquema de la demostración de que anudando
la tira de papel resulta un pentágono regular. Partimos
de que la tira tiene sus bordes paralelos y de que hemos logrado plegarla
de la forma que se indica en la figura.
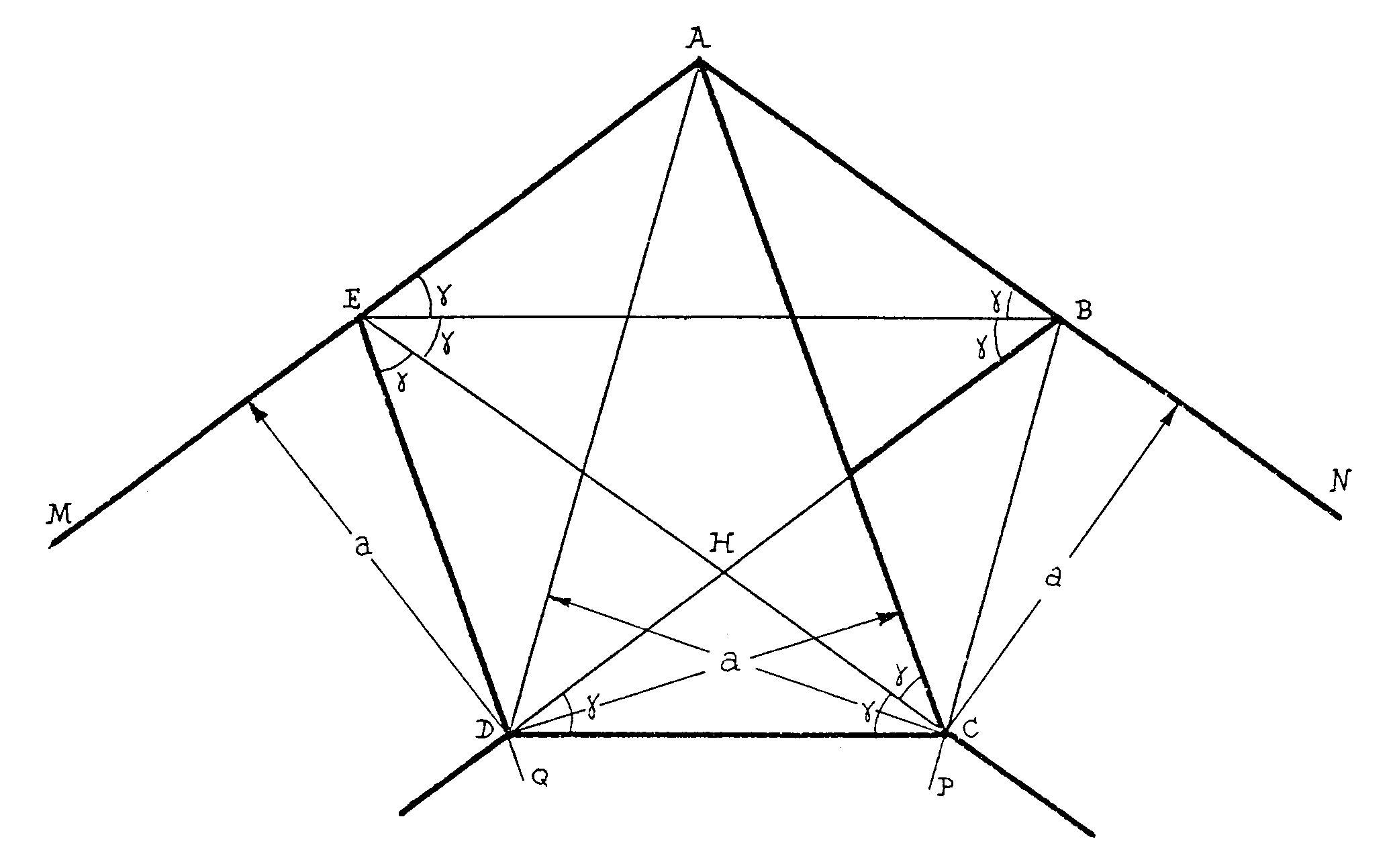
Con facilidad, usando el hecho de que la anchura de la
tira es a, constante, podrás demostrar primero que AC y AD son simétricos
respecto de la mediatriz de DC. Asímismo, son simétricas,
usando el mismo hecho, las rectas AM y AN. Y también CP es simétrica
de DQ. Por tanto AE = AB y, además, son simétricas respecto
de la mediatriz de DC. Con esto queda demostrado que ED = BC y que EB es
paralela a DC. Como ABHE es rombo resulta AEB = HEB. De modo parecido se
demuestra AD = DB y AE = BC por simetría respecto de la mediatriz
de AB. Así ED = DC y HED =BED = 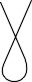 .
Con esto resulta ya fácilmente que todos los ángulos del
pentágono son iguales y los lados también y que
.
Con esto resulta ya fácilmente que todos los ángulos del
pentágono son iguales y los lados también y que 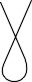 = 36º.
= 36º.



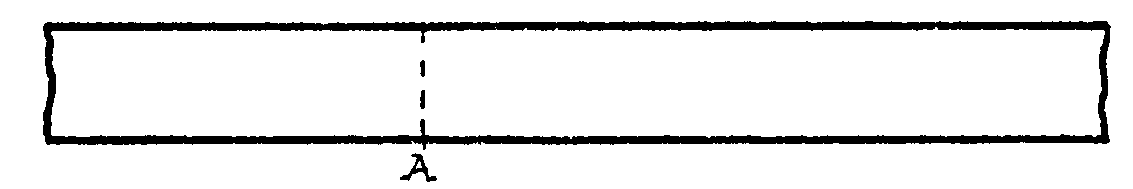
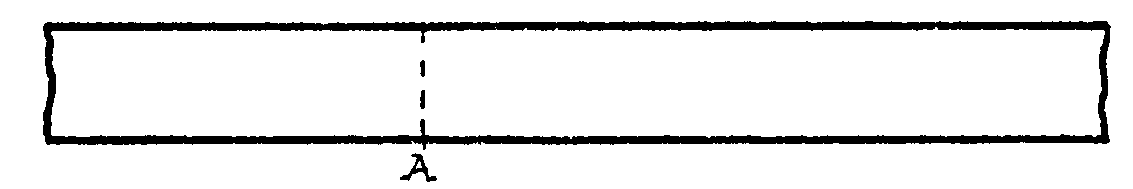
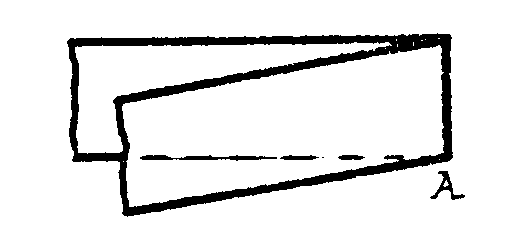
 Observa que el ángulo es de 45º
Observa que el ángulo es de 45º


 Pliegas por los puntos B y C y te resulta el cuadrado.
Pliegas por los puntos B y C y te resulta el cuadrado.








