Experimentos con las rectas
de Wallace-Simson de un triángulo.
Como me ha sucedido varias veces, también en el caso de los experimentos que voy a contar a continuación hubo momentos en que, debido a mi ignorancia, pensé que había descubierto algo importante y que no se conocía. Yo no lo conocía y tuve gran placer y alegría al verlo aparecer delante de mí en toda su belleza. Con el tiempo, al leer más sobre el tema, ví que otros habían pasado mucho antes por el mismo camino, al que habían llegado de diferentes formas. También pude ver que, en algún caso, el resultado se había publicado como un hallazgo curioso,... ¡ más de un siglo después!
Pero de todas formas lo que sí creo haber descubierto
en este caso, a juzgar por los comentarios de algunos colegas que entienden
más que yo de este tema, es una versión de los hechos que
los hace mucho más inteligibles de lo que hasta ahora lo eran. Pero
vayamos por orden.
La historia comienza para mí con el teorema
de Wallace-Simson. Un resultado curioso del escocés Wallace
con el que el asímismo escocés Simson
no tuvo nada que ver. Poncelet y otros geómetras importantes se
lo atribuyeron a Simson, no se sabe muy bien por qué. El hecho es
que el hallazgo se han quedado tradicionalmente con el nombre de Simson,
recta
de Simson, teorema de Simson, si bien más recientemente se va
reconociendo la paternidad de Wallace.
El teorema dice así:

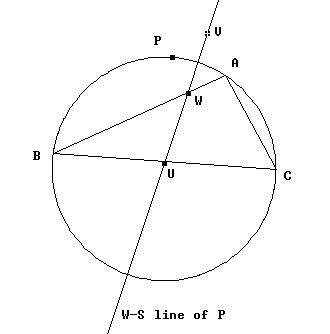
Sea ABC un triángulo arbitrario y K su circunferencia
circunscrita. Para un punto arbitrario de K se trazan las tres proyecciones
ortogonales de P sobre los lados, U sobre a, V sobre b y W sobre c. Entonces
UVW están alineados. La recta UVW se llama la recta de Wallace-Simson
de P con respecto a ABC.
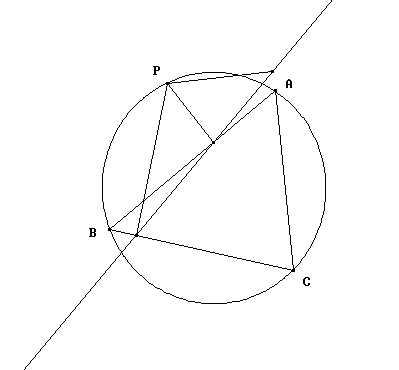
Motivado por un trabajo relacionado con una cierta extensión que yo había obtenido recientemente del teorema clásico de Wallace-Simson publicada en el American Mathematical Monthly (June-July 1999) y que se puede ver aquí, yo me había fabricado unas cuantas funciones DERIVE para trazar la recta de Wallace-Simson correspondiente a un punto P.
Para un triángulo arbitrario inscrito en el
círculo unidad y para cualquier punto sobre su circunferencia DERIVE
me proporcionaba fácilmente la recta de W-S, como se puede ver aquí.
Con tal herramienta en la mano era tentador pensar
en la envolvente de todas las rectas de W-S de un triángulo.
Hice algunos experimentos con muy diferentes triángulos, normales
unos y menos normales otros, trazando 30 rectas de W-S para cada uno de
ellos.
Aquí se pueden ver las figuras correspondientes
a dos de estos experimentos. Los números entre paréntesis
corresponden a la posición en radianes, en la circunferencia unidad,
de los tres vértices del triángulo de cada experimento.
La envolvente para un triángulo "normal".
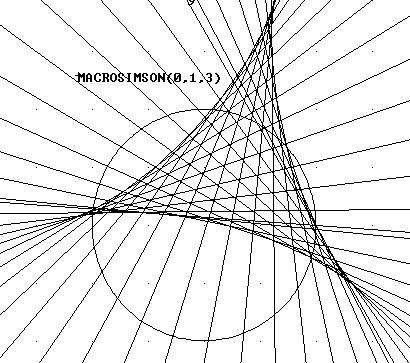
La envolvente para un triángulo un tanto "anormal"

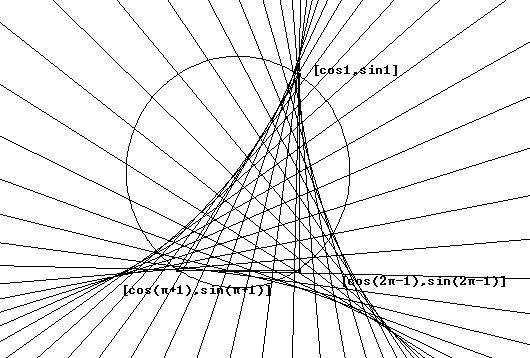
Después de hacer unos cuantos de estos experimentos me parecía "totalmente obvio" que:
(1) La forma de la curva envolvente era siempre la misma, independientemente del triángulo. Tal forma se parecía mucho a la de una hipocicloide tricúspide, que me era una curva familiar por diversos motivos.
(La hipocicloide tricúspide es la curva que describe un punto de una circunferencia de radio r/3 cuando esta circunferencia rueda, sin resbalar, tangente interiormente a una circunferencia de radio r. Una magnífica fuente de información gráfica, analítica,etc... sobre los diferentes tipos de hipocicloides es la página de Eric Weisstein con la que puedes enlazar aquí).
(2) El tamaño de la curva parecía ser siempre el mismo.
(De acuerdo con las medidas que yo tomaba sobre la figura la distancia de un vértice cuspidal al "lado" opuesto era igual al diámetro de la circunferencia circunscrita).
(3) La posición de la curva y su inclinación dependían del triángulo de una forma un tanto extraña, pero incluso para triángulos muy irregulares nunca se separaba demasiado del círculo circunscrito.
Todo esto parecía constituir un bello teorema... de cuya demostración no tenía la más remota idea.
Si todo esto era cierto, me parecía seguro que alguien lo tenía que haber encontrado antes...
Y así era...
En 1856 Jakob
Steiner había demostrado que la
envolvente de las rectas de W-S es una curva de cuarto grado que tiene
tres puntos cuspidales y muchas propiedades muy interesantes. Aquí
se puede ver la primera página del artículo de Steiner.
Muchas propiedades más se han descubierto después.
Y seguro que muchas otras personas han "redescubierto" después de
su primer descubridor esta curva que se suele llamar la deltoide de Steiner.
Al menos es claro que en 1985 D.F. Lawden y G.H. Lawden siguieron el mismo
camino experimental que yo seguí , que construyeron una demostración
trigonométrica relativamente sencilla y que la publicaron sin hacer
ninguna referencia a Steiner
(Envelope of Simpson (sic!) lines, The Mathematical
Gazette, (1985), 296-298).
La curva resulta ser efectivamente una hipocicloide tricúspide.
Tiene el mismo centro que el círculo de Feuerbach (círculo de los nueve puntos) del triángulo ABC y este círculo es tres veces tangente a la deltoide.
La orientación de la deltoide es la misma que
la del triángulo de Morley de ABC, es decir, los vértices
de la deltoide son los vértices de un triángulo equilátero
de lados paralelos a los del triángulo de Morley, aunque la orientación
es la opuesta...
Pero quedaba un desafío interesante...
No parecía existir (y no parece existir, que yo conozca) ninguna demostración sintética fácil de todos estos hechos.
La demostración de Steiner no se puede decir que sea fácil. Y las consideraciones que propone H.F. Baker en su clásica obra An introduction to plane geometry (Cambridge University Press, 1943, Notas 1 y 2 al final) tampoco son muy transparentes.
En el clásico libro de H. Dörrie, 100 Great
Problems of Elementary Mathematics. Their History and Solution (Dover,
New York, 1965, pp. 226-231) se puede encontrar una demostración
de tipo analítico-trigonométrico que, como sucede con tantas
demostraciones analíticas, simplemente comprueban
que lo
que el teorema afirma es verdad, pero que le dejan a uno en la oscuridad
sobre conexiones más profundas.
Puesto que yo tenía unas cuantas herramientas
interesantes de DERIVE para experimentar de diversos modos con la recta
de W-S, con el triángulo de Morley,... traté de ver si con
tales herramientas podría dar con alguna forma de arrojar alguna
luz sobre estas relaciones un tanto misteriosas.
¿Habría alguna forma de hacer evidente por qué todos los triángulos inscritos en el mismo círculo habían de tener las misma envolvente para sus rectas de W-S excepto por la situación de esta curva?
¿Habría alguna
forma de aclarar la aparición de la hipocicloide tricúspide
de una forma directa e inmediata?
Lo razonable parecía ser pensar en alguna transformación del triángulo original manteniendo el círculo circunscrito. Se trataba de ver cuál era entonces el efecto de esta transformación sobre los elementos que intervenían en la situación, rectas de W-S, círculo de Feuerbach, triángulo de Morley,...
La transformación más obvia que a uno
se le ocurre y que se presta a la exploración consiste en mantener
un lado y dejar que el vértice opuesto se mueva sobre la circunferencia
circunscrita fija... pero no parecía darse ninguna relación
fácil entre los diversos elementos citados...
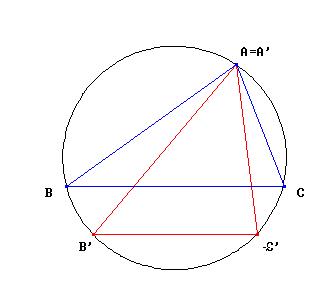
Hasta que se me ocurrió pensar en una transformación
muy sencilla ABC--A'B'C' que parecía arrojar una fuerte luz sobre
todo el misterio. Se me ocurrió dejar fijo el vértice A=A'
y trasladar paralelamente el lado BC a B'C', manteniendo siempre la misma
circunferencia circunscrita. Esta transformación
resultó ser la clave para entenderlo todo directamente.
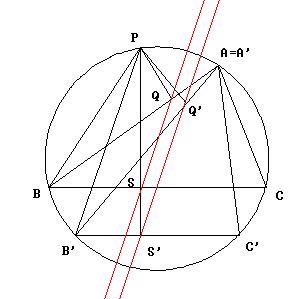
¡La recta de W-S de P con respecto a A'B'C' parecía ser paralela a la recta de W-S de P respecto de ABC!
Y efectivamente es muy fácil demostrar que así es y que la recta de W-S de P respecto de A'B'C' se obtiene trasladando la recta de W-S de P respecto de ABC por la misma traslación paralela que lleva perpendicularmente a BC la recta BC a la recta B'C'.
Por otra parte, como el círculo
de Feuerbach (círculo de los nueve puntos) pasa por el punto medio
de los lados y por los pies de las alturas y su radio es la mitad del radio
de la circunferencia circunscrita, resulta sencillo ver que el círculo
de Feuerbach de A'B'C' se obtiene del de ABC por la misma traslación.
Este conjunto de relaciones confirmaba plenamente que esta transformación era la llave para el estudio de la envolvente que buscaba.
AHORA RESULTABA CLARO QUE LA ENVOLVENTE DE LAS RECTAS DE W-S PARA A'B'C' SE OBTIENE MEDIANTE ESTA TRASLACION PARALELA A PARTIR DE LA ENVOLVENTE DE LAS RECTAS DE W-S DE ABC.
Aquí se pueden ver las envolventes correspondientes a dos triángulos del tipo ABC y A'B'C'.

Quedaba ahora una cuestión natural:
¿Podríamos utilizar tal vez otra transformación parecida a la anterior que llevase A'B'C' a un triángulo A''B''C'' para el cual la cuestión de la envolvente fuera realmente sencilla de demostrar?
¿Sería posible
hacer que A''B''C'' fuera un triángulo equilátero? Entonces
parece que la demostración de que la envolvente es una hipocicloide
habría de ser muy sencilla.
¡SI!! ¡Y se pueden determinar exactamente cuáles son las traslaciones que lo consiguen!
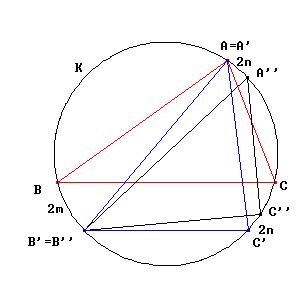
Hemos obtenido A'B'C'. Ahora dejamos fijo B' y tratamos
de clacular m y n en la figura de modo que los ángulos A''=B''=C''=60º
(para ello basta tomar m = (180-B-2C)/3, n = (B - C)/3). En ese caso el
valor del ángulo que forman B'' C'' y BC es exactamente (C-B)/3,
lo cual será interesante más adelante al examinar las relaciones
con el triángulo de Morley.
Ahora sí que resulta evidente
por qué todos los triángulos inscritos en la misma circunferencia
tienen como envolvente de sus rectas de W-S la misma curva en forma y en
tamaño, cambiando sólo en posición.
Y también es claro por
qué el centro de la deltoide es el centro del círculo de
Feuerbach y por qué este es tres veces tangente a la deltoide.
La demostración del hecho
de que la deltoide coincide con la hipocicloide tricúspide queda
reducida al caso del triángulo equilátero y esto no es una
tarea difícil, incluso en terminos de geometría sintética.
Pero había varias cuestiones aún pendientes:
(1) El centro de la envolvente es el centro del círculo de Feuerbach, pero ¿cómo se determina la posición de la envolvente?
(2) Se podría arrojar alguna luz sobre la extraña relación con el triángulo de Morley?
(Se pueden consultar las Notas
1 y 2 al final de H.F. Baker, An introduction to plane geometry,
Cambridge University Press, 1943)
Puesto que para el estudio experimental del triángulo de Morley me había construído unas funciones DERIVE que me proporcionaban el triángulo de Morley de un triángulo cualquierapodía ahora tratar de hacer experimentos para averiguar cómo se transformaba el triángulo de Morley por la transformación ABC-A'B'C'. He aquí un ejemplo de estos experimentos, para ver cómo es afectado el triángulo de Morley:
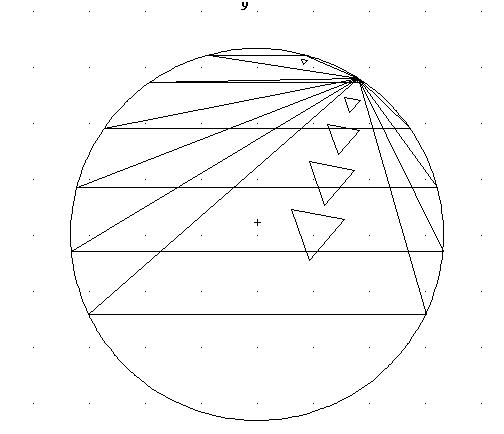
La conjetura es obvia. La transformación preserva la dirección de los lados del triángulo de Morley. ¿Se puede demostrar?
¡SI!
Se puede demostrar (ver, por ejemplo, la demostración
del teorema de Morley de Naraniengar en el libro Geometry Revisited de
Coxeter y Greitzer, ) que el ángulo que el lado NP del triángulo
de Morley forma con el BC es (C-B)/3, y es muy claro que esta magnitud
no varía por la transformación que hemos introducido.
¡Y además, (C-B)/3 es precisamente el
ángulo que nos ha resultado antes al tratar de convertir el triángulo
arbitrario ABC en equilátero mediante la aplicación sucesiva
de dos transformaciones del tipo de las que hemos introducido en nuestro
razonamiento!
Esta observación resuelve nuestras dos últimas cuestiones:
El triángulo de Morley y y el que forman los
vértices de la deltoide tienen lados paralelos pero orientación
opuesta. La posición de la deltoide de Steiner queda así
completamente determinada, si bien también queda claro que, dado
un triángulo arbitrario ABC, si bien el centro de la deltoide se
puede construir con regla y compás (es el centro del círculo
de Feuerbach), no se pueden construir con regla y compás los puntos
cuspidales de ella, ya que ello, como la construcción del triángulo
de Morley, equivale en general a la trisección del ángulo.
+++++++++++++++++++++++++++++++++++++++++++++++++++
Muchas otras propiedades interesantes de la deltoide se pueden obtener mediante experimentos y cálculos apropiados con DERIVE. Por ejemplo las siguientes que quedan aquí para tu propia experimentación y comprobación.
(1) El punto medio del segmento de tangente a la deltoide determinado por los otros puntos de intersección con la deltoide misma se encuentra sobre la circunferencia de Feuerbach.
(2) Un punto se mueve sobre una recta con un movimiento armónico, es decir su posición respecto de un punto de la recta está dada por una expresión de la forma a+bsint. Una recta ligada a este punto gira de tal modo que el ángulo de las dos rectas es t/2. Entonces la envolvente de la segunda recta es una hipocicloide tricúspide, cuyos elementos quedan determinados fácilmente mediante las consideraciones anteriores.
(3) Un punto tiene coordenadas cartesianas (cost, sint). Una recta ligada a él gira formando un ángulo t/2 con el eje Ox. Entonces la envolvente de todas estas rectas es una hipocicloide tricúspide.
Las tres observaciones anteriores son teoremas cuya demostración no es muy complicada. La siguiente observación parece serlo también. Anímate a comprobarlo.
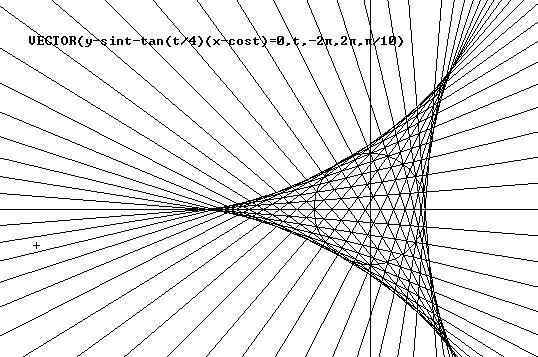
(4) Un punto tiene coordenadas cartesianas (cost, sint). Una recta ligada a él gira formando un ángulo t/4 con el eje Ox. Entonces la envolvente de todas estas rectas parece ser es una hipocicloide tricúspide.
He aquí una figura que corresponde a este último
experimento