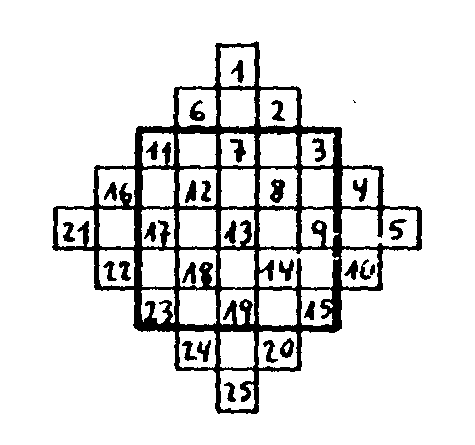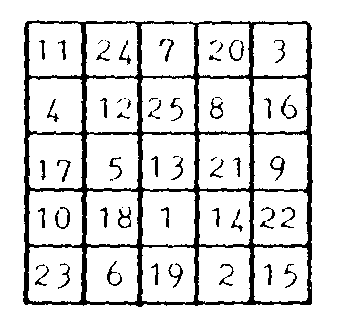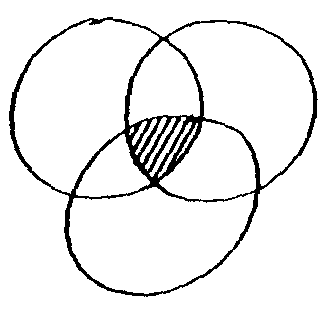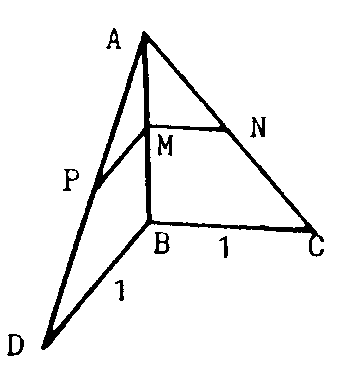Publicado
en
Actas de las IV Jornadas sobre
Aprendizaje y Enseñanza de las Matemáticas
Santa Cruz de Tenerife, 10-14
Septiembre 1984
Sociedad Canaria de Profesores de
Matemáticas Isaac Newton
(Agradezco a Jorge Moreno Pérez su ayuda para hacer este
artículo asequible a través de la red)
JUEGOS MATEMÁTICOS EN LA ENSEÑANZA
Miguel de Guzmán
Facultad de Matemáticas
Universidad Complutense de Madrid
A good mathematical joke is
better and better mathematics
than a dozen mediocre papers
(J.E. Littlewood, A Mathematician´s Miscellany).
Indice
1. MATEMATICAS
Y JUEGOS.
Impacto
de los juegos en la historia de la matemática.
El
fundamento matemático de los juegos.
Matemáticas
con sabor a juego.
Consecuencias
para la didáctica de la matemática.
Notas
sobre la literatura clásica sobre juegos.
2.
UTILIZACION DE LOS JUEGOS EN LA ENSEÑANZA.
A.- Directrices heurísticas basadas en juegos.
1. ANTES
DE HACER, TRATARÉ DE ENTENDER.
2. TRAMARÉ UNA ESTRATEGIA,
O VARIAS.
3. MIRARÉ
SI MI ESTRATEGIA ME LLEVA AL FINAL.
4. SACARÉ JUGO AL JUEGO.
Ejemplos
B. Directrices temáticas para el uso de los Juegos.
1. SORPRESAS
MATEMÁTICAS.
2. CUENTOS CON CUENTAS.
3. SISTEMAS DE NUMERACION.
4. CRITERIOS DE
DIVISIBILIDAD.
5. INDUCCIÓN.
6. CONTAR SIN CONTAR.
7. DEDUCCIÓN LÓGICA
8. ELEMENTAL, QUERIDO WATSON.
9. SIMETRÍA.
10. HAZTE UN DIBUJO.
11. UTILIZACIÓN DE
COLORES.
12. COMENZAR
POR LO FÁCIL AYUDA A RESOLVER LO DIFÍCIL
13. PIENSA
AL REVÉS. SUPONGAMOS EL PROBLEMA RESUELTO.
14. SOLITARIOS MATEMÁTICOS.
15. PARTIDOS MATEMÁTICOS.
16. ANALOGÍAS ESCONDIDAS.
17. FALACIAS.
18. FELIZ IDEA.
3.
ALGUNAS INDICACIONES BIBLIOGRÁFICAS.
1. MATEMATICAS
Y JUEGOS.
¿Dónde termina el juego
y dónde comienza la matemática seria? Una pregunta capciosa
que admite múltiples respuestas. Para muchos de los que ven la matemática
desde fuera, ésta, mortalmente aburrida, nada tiene que ver con
el juego. En cambio, para los más de entre los matemáticos,
la matemática nunca deja totalmente de ser un juego, aunque además
de ello pueda ser otras muchas cosas.
El juego bueno, el que no depende
de la fuerza o maña físicas, el juego que tiene bien definidas
sus reglas y que posee cierta riqueza de movimientos, suele prestarse muy
frecuentemente a un tipo de análisis intelectual cuyas características
son muy semejantes a las que presenta el desarrollo matemático.
Las diferentes partes de la matemática tienen sus piezas, los objetos
de los que se ocupa, bien determinados en su comportamiento mutuo a través
de las definiciones de la teoría. Las reglas válidas de manejo
de estas piezas son dadas por sus definiciones y por todos los procedimientos
de razonamiento admitidos como válidos en el campo. Cuando la teoría
es elemental, estos no son muchos ni muy complicados y se adquieren bien
pronto, lo cual no quiere decir que el juego sea trivial. Elemental quiere
decir cerca de los elementos iniciales y no necesariamente simple. Existen
problemas elementales desproporcionadamente complicados con respecto a
su enunciado. Un ejemplo lo constituye el problema de averiguar el mínimo
de las figuras en las que una aguja unitaria puede ser invertida en el
plano por movimientos continuos. Cuando la teoría no es elemental
es generalmente porque las reglas usuales del juego se han desarrollado
extraordinariamente en número y en complejidad y es necesario un
intenso esfuerzo para hacerse con ellas y emplearlas adecuadamente. Son
herramientas muy poderosas que se han ido elaborando, cada vez más
sofisticadas, a lo largo de los siglos. Tal es, por ejemplo, la teoría
de la medida e integral de Lebesgue en el análisis superior.
La matemática así concebida
es un verdadero juego que presenta el mismo tipo de estímulos y
de actividad que se da en el resto de los juegos intelectuales. Uno aprende
las reglas, estudia las jugadas fundamentales, experimentando en partidas
sencillas, observa a fondo las partidas de los grandes jugadores, sus mejores
teoremas, tratando de asimilar sus procedimientos para usarlos en condiciones
parecidas, trata finalmente de participar más activamente enfrentándose
a los problemas nuevos que surgen constantemente debido a la riqueza del
juego, o a los problemas viejos aún abiertos esperando que alguna
idea feliz le lleve a ensamblar de modo original y útil herramientas
ya existentes o a crear alguna herramienta nueva que conduzca a la solución
del problema.
Por esto no es de extrañar
en absoluto que muchos de los grandes matemáticos de todos los tiempos
hayan sido agudos observadores de los juegos, participando muy activamente
en ellos, y que muchas de sus elucubraciones, precisamente por ese entreveramiento
peculiar de juego y matemática, que a veces los hace indiscernibles,
hayan dado lugar a nuevos campos y modos de pensar en lo que hoy consideramos
matemática profundamente seria.
Impacto
de los juegos en la historia de la matemática.
La historia antigua no ha sido inclinada
a preservar sino los elementos solemnes de la actividad científica,
pero uno no puede menos de sospechar que muchas de las profundas cavilaciones
de los pitagóricos, por ejemplo alrededor de los números,
tuvieron lugar jugando con configuraciones diferentes que formaban con
las piedras. El llamado problema bovino de Arquímedes, álgebra
hecha con procedimientos rudimentarios, tiene un cierto sabor lúdico,
así como otras muchas de sus creaciones matemáticas originales.
Euclides fue, al parecer, no sólo el primer gran pedagogo
que supo utilizar, en una obra perdida llamada Pseudaria (Libro
de Engaños), el gran valor didáctico en matemática
de la sorpresa producida por la falacia y la aporía.
En la Edad Media Leonardo de Pisa
(ca.1170-ca.1250), mejor conocido hoy y entonces como Fibonaccí,
cultivó una matemática numérica con sabor a juego
con la que, gracias a las técnicas aprendidas de los árabes,
asombró poderosamente a sus contemporáneos hasta el punto
de ser proclamado oficialmente por el emperador Federico II como Stupor
Mundí.
En la Edad Moderna Geronimo Cardano
(1501-1576), el mejor matemático de su tiempo, escribió el
Líber de ludo aleae, un libro sobre juegos de azar, con el
que se anticipó en más de un siglo a Pascal y Fermat en el
tratamiento matemático de la probabilidad. En su tiempo, como tomando
parte en este espíritu lúdico, los duelos medievales a base
de lanza y escudo dieron paso a los duelos intelectuales consistentes en
resolver ecuaciones algebraicas cada vez más difíciles, con
la participación masiva, y más o menos deportiva, de la población
estudiantil, de Cardano mismo y otros contendientes famosos como Tartaglia
y Ferrari.
El famoso problema del Caballero de
Meré, consistente en saber cómo deben ser las apuestas de
dos jugadores que, habiendo de alcanzar n puntos con sus dados, uno ha
obtenido p y el otro q puntos en una primera jugada, fue propuesto por
Antoine Gobaud, Caballero de Meré (1610-1685) a Pascal (1623-1662).
De la correspondencia entre éste y Fermat (1601-1665) a propósito
del problema surgió la moderna teoría de la probabilidad.
Leibniz (1646-1716) fue un gran promotor
de la actividad lúdica intelectual: "Nunca son los hobres más
ingeniosos que en la invención de los juegos... Sería deseable
que se hiciese un curso entero de juegos, tratados matemáticamente",
escribía en una carta en 1715. Y en particular comenta en otra carta
en 1716 lo mucho que le agrada el ya entonces popular solitario de la cruz,
y lo interesante que le resulta el jugarlo al revés.
En 1735, Euler (1707-1783), oyó
hablar del problema de los siete puentes de Königsberg, sobre la posibilidad
de organizar un paseo que cruzase todos y cada uno de los puentes una sola
vez (camino euleriano). Su solución constituyó el comienzo
vigoroso de una nueva rama de la matemática, la teoría de
grafos y con ella de la topología general.
También el espíritu
matemático de la época de Euler participaba fuertemente del
ánimo competitivo de la época de Cardano. Johann Bernoulli
(1667-1748) lanza el problema de la braquistócrona como un reto
a los mejores matemáticos de su tiempo. En este duelo participaron
con ardor nada menos que Jakod Bernoulli (creador, precisamente con su
solución al problema, del cálculo de variaciones) Leibniz,
Newton y Huygens.
Se cuenta que Hamilton (1805-1865)
sólo recibió dinero directamente por una de sus publicaciones
y ésta consistió precisamente en un juego matemático
que comercializó con el nombre de Viaje por el Mundo. Se
trataba de efectuar por todos los vértices de un dodecaedro regular,
las ciudades de ese mundo, un viaje que no repitiese visitas a ciudades
circulando por los bordes del dodecaedro y volviendo al punto de partida
(camino hamiltoniano). Esto ha dado lugar a un problema interesante en
teoría de grafos que admiten un camino hamiltoniano.
Los biógrafos de Gauss
(1777-1855) cuentan que el Princeps Mathematicorum era un gran aficionado
a jugar a las cartas y que cada día anotaba cuidadosamente las manos
que recibía para analizarlas después estadísticamente.
Hilbert (1862-1943) uno de
los grandes matemáticos de nuestro tiempo es responsable de un teorema
que tiene que ver con los juegos de disección: dos polígonos
de la misma área admiten disecciones en el mismo número de
triángulos iguales.
John von Neumann (1903-1957),
otro de los matemáticos más importantes de nuestro siglo,
escribió con Oskar Morgenstern en 1944 un libro titulado Teoría
de Juegos y Conducta Económica. En él analizan los juegos
de estrategia donde aparece en particular el teorema de minimax,
pieza fundamental para los desarrollos matemáticos sobre el comportamiento
económico.
Según cuenta Martin Gardner,
Albert Einstein (1879-1955), tenía toda una estantería
de su biblioteca particular dedicada a libros sobre juegos matemáticos.
El
fundamento matemático de los juegos.
Estas muestras del interés
de los matemáticos de todos los tiempos por los juegos matemáticos,
que se prodrían ciertamente multiplicar, apuntan a un hecho indudable
con dos vertientes. Por una parte son muchos los juegos con un contenido
matemático profundo y sugerente y por otra parte una gran porción
de la matemática de todos los tiempos tiene un sabor lúdico
que la asimila extraordinariamente al juego.
El primer aspecto se puede poner bien
de manifiesto sin más que ojear un poco el repertorio de juegos
más conocidos. La aritmética está inmersa en
los cuadrados mágicos, cambios de monedas, juegos sobre pesadas,
adivinación de números,... La teoría elemental
de números es la base de muchos juegos de adivinación
fundamentados en criterios de divisibilidad, aparece en juegos que implican
diferentes sistemas de numeración, en juegos emparentados con el
Nim,... La combinatoria es el núcleo básico de todos
los juegos en los que se pide enumerar las distintas formas de realizar
una tarea, muchos de ellos sin resolver aún, como el de averiguar
el número de formas distintas de plegar una tira de sellos, el problema
del viajante,... El álgebra interviene en muchos acertijos
sobre edades, medidas, en el famoso juego de los 15, en el problema de
las ocho reinas,... La teoría de grupos, en particular el
grupo de Klein, es una herramienta importante para analizar ciertos juegos
con fichas en un tablero en los que se "come al saltar al modo de las damas.
La teoría de grafos es una de las herramientas que aparece
más frecuentemente en el análisis matemático de los
juegos. Nació con los puentes de Königsberg, se encuentra en
el juego de Hamilton, da la estrategia adecuada para los acertijos de cruces
de ríos, como el del pastor, la oveja, la col y el lobo, el de los
maridos celosos, y resuelve también muchos otros más modernos
como el de los cuatro cubos de la Locura Instantánea... La teoría
de matrices está íntimamente relacionada también
con los grafos y juegos emparentados con ellos. Diversas formas de topología
aparecen tanto en juegos de sabor antiguo, como el de las tres granjas
y tres pozos, como en juegos más modernos como los relacionados
con la banda de Möbius, problemas de coloración, nudos, rompecabezas
de alambres y anillas... La teoría del punto fijo es básica
en algunos acertijos profundos y sorprendentes como el del monje que sube
a la montaña, el pañuelo que se arruga y se coloca sobre
una réplica suya sin arrugar,... La geometría aparece
de innumerables formas en falacias, diseciones, transformación de
configuraciones con cerillas, poliominós planos y espaciales,...
La probabilidad es, por supuesto, la base de todos los juegos de
azar, de los que precisamente nació. La lógica da
lugar a un sinfín de acertijos y paradojas muy interesantes que
llaman la atención por su profundidad y por la luz que arrojan sobre
la estructura misma del pensamiento y del lenguaje.
Matemáticas
con sabor a juego.
Por otra parte resulta igualmente
fácil señalar problemas y resultados profundos de la matemática
que rezuman sabor a juego. Citaré unos pocos entresacados de la
matemática más o menos contemporánea.
El teorema de Ramsey, en su
forma más elemental, afirma que si tenemos 6 puntos sobre una circunferencia,
los unimos dos a dos, y coloreamos arbitrariamente los segmentos que resultan
de rojo o de verde, entonces necesariamente hay al final un triángulo
con tales segmentos por los lados que tiene sus tres lados del mismo color.
El lema de Sperner, importante
en la teoría del punto fijo, afirma que si en un triángulo
ABC se efectúa una triangulación (Una partición en
un número finito de triángulos tales que cada dos de ellos
tienen en común un lado, un vértice, o nada) y se nombran
los vértices de los triángulos de la triangulación
con A, B, C, de modo que en el lado AB no haya más que las letras
A ó B, en el AC nada más que A ó C y en BC nada más
que B ó C, entonces necesariamente hay un triángulo de la
triangulación que se llama ABC.
El teorema de Helly afirma
que si en un plano hay un número cualquiera de conjuntos convexos
y compactos tales que cada tres tienen un punto en común, entonces
todos ellos tienen al menos un punto en común.
El problema de Lebesgue, aún
sin resolver, pregunta por el mínimo del área de aquellas
figuras capaces de cubrir cualquier conjunto del plano de diámetro
menor o igual que 1.
El siguiente problema de la aguja
en un convexo tridimensional está también aún
abierto: ¿Cuál es el cuerpo convexo de volumen mínimo
capaz de albergar una aguja de longitud 1 paralela a cada direción
dada? Se sospecha, por analogía con el caso bidimensional, que es
el tetraedro regular de altura 1, pero no hay demostración de ello.
Consecuencias
para la didáctica de la matemática.
La matemática es, en gran parte,
juego, y el juego puede, en muchas ocasiones, analizarse mediante instrumento
matemáticos. Pero, por supuesto, existen diferencias substanciales
entre la práctica del juego y la de la matemática. Generalmente
las reglas del juego no requieren introducciones largas, complicadas, ni
tediosas. En el juego se busca la diversión y la posibilidad de
entrar en acción rápidamente. Muchos problemas matemáticos,
incluso algunos muy profundos, permiten también una introducción
sencilla y una posibilidad de acción con instrumentos bien ingenuos,
pero la matemática no es sólo diversión, sino ciencia
e instrumento de exploración de su realidad propia mental y externa
y así ha de plantearse, no las preguntas que quiere, sino las que
su realidad le plantea de modo natural. Por eso muchas de sus cuestiones
espontáneas le estimulan a crear instrumentos sutiles cuya adquisición
no es tarea liviana. Sin embargo, es claro que, especialmente en la tarea
de iniciar a los más jóvenes en la labor matemática,
el sabor a juego puede impregnar de tal modo el trabajo, que lo haga mucho
más motivado, estimulante, incluso agradable y, para algunos, aún
apasionante. De hecho, como veremos, han sido numerosos los intentos de
presentar sistemáticamente los principios matemáticos que
rigen muchos de los juegos de todas las épocas, a fin de poner más
en claro las conexiones entre juegos y matemáticas. Desafortunadamente
para el desarrollo científico en nuestro país, la aportación
española en este campo ha sido casi nula. Nuestros científicos
y nuestros enseñantes se han tomado demasiado en serio su ciencia
y su enseñanza y han considerado ligero y casquivano cualquier intento
de mezclar placer con deber. Sería deseable que nuestros profesores,
con una visión más abierta y más responsable, aprendieran
a aprovechar los estímulos y motivaciones que este espíritu
de juego puede ser capaz de infundir en sus estudiantes.
Notas
sobre la literatura clásica sobre juegos.
Los datos que siguen sobre la historia
de la literatura sobre recreaciones matemáticas están tomados
fundamentalmente del artículo de Shaaf en la Encyclopaedia
Britannica titulado Number Games and Other Mathematical Recreations,
que contiene una excelente exposición delos juegos más significativos
y de las obras más importantes. Pienso que los más seriamente
aficionados a los juegos matemáticos agradecerán estas breves
notas y que servirán al mismo tiempo para que los más escépticos
ppuedan comprobar al menos con qué tesón ha sido y es cultivado
el campo en otros paises.
Aunque en la Edad Media y comienzos
de la Moderna se dieron algunos intentos esporádicos de formalización
y análisis matemático de juegos, con Fibonacci (1202), Robert
Recorde (1542) y Geronimo Cardano (1545), el gran primer sistematizador
de donde bebieron abundantemente posteriores imitadores fue Claude-Gaspar
Bachet de Méziriac, quien en 1612 publicó su obra de
vanguardia en este campo Problémes plaisans et delectables qui
se font par les nombres. A él mismo se debe también la
publicación en francés de Diophanti, traducción
de un texto griego sobre teoría de números que ejerció
un gran influjo sobre la historia de la matemática, sobre todo a
través de Fermat. El libro de recreaciones de Bachet estaba basado
sobre todo en propiedades aritméticas y contiene los problemas más
clásicos sobre juegos de cartas, relojes, determinación del
número de pesas para pesar 1, 2, 3,..., 40 kilos, problemas de cruces,...
En 1624 un jesuíta francés,
Jean Leurechon, escribió bajo el seudónimo de van Etten,
una obra, Recréations Mathématiques, fuertemente basada en
la de Bachet, pero que tuvo mucho más éxito que la de éste,
alcanzando las 30 ediciones ya en 1700. La obra de van Etten , una
obra, Recreátions Mathématiques, fuertemente basada
en la de Bachet, pero que tuvo más exito que la de éste,
alcanzando las 30 ediciones ya en 1700. La obra de van Etten fue modelo
para sus continuadores Claude Mydorge (1630), en Francia, y Daniel
Schwenter, en Alemania. Este último, profesor de hebreo, lenguas
orientales y matemáticas, añadió gran cantidad de
material copilado por él mismo. Su obra póstuma apareció
en 1636 con el título Deliciae PhysicoMathematicae oder Mathematische
und Philosophische Erquickstunden y la reedición de ella en
1651-1653 fue por algún tiempo la obra más completa en su
género.
Mientras tanto había aparecido
en Italia en 1641-1642 la obra en dos volúmenes bajo el complicado
título Apiaria Universae philosophiae Mathematicae, in quibus
paradoxa et nova pleraque machinamenta exhiebntur, escrita por el jesuíta
Mario Bettini. Fue seguida en 1660 por un tercer volumen Recreationum Mathematicarum
Apiaria Novissima...
En Inglaterra William Leybourn
publica en 1694 un libro a medio camino entre el texto y la recreación,
con la intención de "apartar a la juventud de los vicios propios
a los que es inclinada". Su título fue Pleasure with Profit:
Consisting of Recreations of Divers Kinds...
La obra que realmente marca la pauta
para los muchos autores que aparecerán en los siglos 18 y 19 fue
la de Jacques Ozanam, quien en 1694 publicó Récréatiions
Mathématiques et Physiques, obra inspirada en las de Bachet, Leurechon,
Mydorge y Schwenter, que fue revisada más tarde por el historiador
de la matemática Montucla.
Al final del siglo 19 aparecen los
cuatro volúmenes de Edouard Lucas; especialista en teoría
de números, titulados Récréations mathematiques
(1882-1894), que pasa a ser la obra clásica durante algún
tiempo. Contemporaneo de Lucas es Lewis Carroll, el autor de Alicia,
gran aficionado a los puzzles lógicos y juegos matemáticos
quien publicó, entre otras cosas, Pillow Problems y A Tangled
Tale (1885-1895).
En la primera mitad del siglo 20 los
nombres más importantes en América son los de los dos Sam
Loyd, padre e hijo, grandes especialestas en puzzles mecánicos,
autores del famosísimo juego de los 15, que en su tiempo causó
un furor parecido al del cubo de Rubik en nuestros días. En Alemania
se destacan Hermann Schubert con sus Zwölf Gedulspiele
(1907-1909) en tres volúmenes, así como Wilhelm Ahrens
con sus dos volúmenes Mathematische Unterhaltungen und Spiele
(1904-1920). En Inglaterra se destacan Henry Dudeney (1917-1967)
y sobre todo la gran obra de W.W.Rouse Ball, Mathematical Recreations
and Essays (1892, primera edición), otro de los clásicos,
con gran erudición histórica, en cuyas páginas puede
apreciarse documentadamente, a través de las numerosas notas, el
impacto de los juegos sobre los matemáticos y las matemáticas
de todos los tiempos. El geómetra H.S.M. Coxeter revisó
en 1938 la undécima edición. En Bélgica hay que destacar
a Maurice Kraitchik, editor de la revista Sphinx y compilador de
varios libros entre 1900 y 1942. En Holanda se destaca también Fred.
Schuh, con su obra Wonderlijke Problemen, publicada en 1943.
A partir de los años 50 Martin
Gardner comenzó a publicar con gran éxito su artículo
mensual en las páginas de Scientific American y su nombre,
gracias a la difusión de esa revista y a las compilaciones sucesivas,
ocho hasta el presente, de sus mejores artículos, ha llenado con
enorme éxito el campo hasta finales de los años 70. De las
obras más recientes hay que destacaar especialmente la de Berlekamp,
Conway y Guy, titulada Winning Ways, en dos volúmenes,
publicada en 1982, que por su amplitud, sistematización y profundidad,
alcanzará sin duda un gran éxito entre los aficionados más
concienzudos.
2.
UTILIZACION DE LOS JUEGOS EN LA ENSEÑANZA.
¿Se pueden utilizar los juegos
matemáticos con provecho en la enseñanza? ¿De qué
forma? ¿Qué juegos? ¿Qué objetivos pueden conseguirse
a través de los juegos?
Los juegos tienen un carácter
fundamental de pasatiempo y diversión. Para eso se han hecho y ese
es el cometido básico que desempeñan. Por eso es natural
que haya mucho receloso de su empleo en la enseñanza. "El alumno,
-piensa-, se queda con el pasatiempo que, eso sí, le puede comer
el coco totalmente y se olvida de todo lo demás. Para lo que se
pretende, es una miserable pérdida de tiempo".
A mi parecer, en cambio, ese mismo
elemento de pasatiempo y diversión que el juego tiene esencialmente,
debería ser un motivo más para utilizarlo generosamente.
¿Por qué no paliar la mortal seriedad de muchas de nuestras
clases con una sonrisa? Si cada día ofreciésemos a nuestros
alumnos, junto con el rollo cotidiano, un elemento de diversión,
incluso aunque no tuviese nada que ver con el contenido de nuestra enseñanza,
el conjunto de nuestra clase y de nuestras mismas relaciones personales
con nuestros alumnos variarían favorablemente.
Pero es que además sucede que,
por algunas de las razones apuntadas antes, relativas a la semejanza de
estructura del juego mismo y de la matemática, avaladas por la historia
misma de la matemática y de los juegos, y por otras razones que
señalaré a continuación, el juego bien escogido y
bien explotado puede ser un elemento auxiliar de gran eficacia para lograr
algunos de los objetivos de nuestra enseñanza más eficazmente.
En mi opinión, el objetivo
primordial de la enseñanza básica y media no consiste en
embutir en la mente del niño un amasijo de información que,
pensamos, le va a ser muy necesaria como ciudadano en nuestra sociedad.
El objetivo fundamental consiste en ayudarle a desarrollar su mente y sus
potencialidades intelectuales, sensitivas, afectivas, físicas, de
modo armonioso. Y para ello nuestro instrumento principal debe consistir
en el estímulo de su propia acción, colocándole en
situaciones que fomenten el ejercicio de aquellas actividades que mejor
pueden conducir a la adquisición de las actitudes básicas
más características que se pretende transmitir con el cultivo
de cada materia.
Por la semejanza de estructura entre
el juego y la matemática, es claro que existen muchos tipos de actividad
y muchas actitudes fundamentales comunes que pueden ejercitarse escogiendo
juegos adecuados tan bien o mejor que escogiendo contenidos matemáticos
de apariencia más seria, en muchos casos con claras ventajas de
tipo psicológico y motivacional para el juego sobre los contenidos
propiamente matemáticos.
Es un hecho frecuente que muchas personas
que se declaran incapaces de toda la vida para la matemática, disfrutan
intensamente con puzzles y juegos cuya estructura en poco difere de la
matemática. Existen en ellas claros bloqueos psicológicos
que nublan su mente en cuanto se percatan de que una cuestión que
se les propone, mucho más sencilla tal vez que el juego que practican,
tiene que ver con el teorema de Pitágoras. Estos bloqueos son causados
muy frecuentemente en la niñez, donde a absurdas preguntas iniciales
totalmente inmotivadas sguían respuestas aparentemente inconexas
que hacían de la matemática una madeja inextricable cada
vez más absurda y complicada.
Bien se puede pensar que muchas de
estas personas, adecuadamente motivadas desde un principio, tal vez a través
de esos mismos elementos lúdicos que están descargados del
peso psicológico y de la seriedad temible de la matemática
oficial, se mostrarían, ante la ciencia en general y ante la matemática
misma en particular, tan inteligentes como corresponde al éxito
de su actividad en otros campos diferentes.
Es claro que no todos los juegos que
se encuentran en los libros de recreaciones matemáticas se prestan
igualmente al aprovechamiento didáctico. Muchos son meras charadas
y acertijos ingeniosos. Muchos otros se basan en la confusión intencionada
del enunciado al modo de los oráculos sibilinos y dejan al final
una impresión de mera tomadura de pelo. En otros casos la solución
de la impresión de haber llegado por revelación divina que
no cabe fácilmente en un esquema de pensamiento que pueda conducir
a un método. Pero, como veremos, hay juegos que, de forma natural,
resultan asquibles a una manipulación muy semejante a la que se
lleva a cabo en la resolución sistemática de problemas matemáticos
y que encierran lecciones profundamente valiosas.
Es mi intención presentar a
continuación dos esquemas de posible utilización de los juegos
en la enseñanza. El primero consiste en un ensayo de desarrollo
heurístico a través de los juegos. Trataré de poner
de manifiesto cómo lo que, a mi parecer, constituye la savia de
las matemáticas y la manera más efectiva de acercamiento
a ellas desde el punto de vista didáctico, la resolución
de problemas, puede aprovecharse de la actividad con juegos bien escogidos.
El segundo esquema presenta, a través de un listado de temas, actitudes
y actividades matemáticas, cómo los juegos pueden utilizarse
para motivar, enriquecer e iluminar la ocupación con ellas.
Lo que sobre todo deberíamos
proporcionar a nuestros alumnos a través de las matemáticas
es la posibilidad de hacerse con hábitos de pensamiento adecuados
para la resolución de problemas, matemáticos y no matemáticos.
¿De qué les puede servir hacer un hueco en su mente en el
que quepan unos cuantos teoremas y propiedades relativas a entes con poco
significado si luego van a dejarlos allí herméticamente emparedados?
A la resolución de problemas se le ha llamado, con razón
el corazón de las matemáticas, pues ahí es donde se
puede adquirir el verdadero sabor que ha atraído y atrae a losmatemáticos
de todas las épocas. Del enfrentamiento con problemas adecuados
es de donde pueden resultar motivaciones, actitudes, hábitos, ideas
para el desarrollo de herramientas apropiadas, en una palabra, la vida
propia de las matemáticas. Muchos de estos elementos pueden adquirirse
igualmente en el enfrentamiento con los problemas que constituyen los juegos
matemáticos.
Lo que sigue viene a ser, en sus líneas
generales, un calco de las directrices fundamentales de la famosa obra
de Polya ¿Cómo Resolverlo?, ilustradas aquí con algunos
juegos que a mí, espigando en la literatura, me han parecido adecuados.
El objetivo de este esquema consiste simplemente en tratar de poner bien
patente la semejanza de actitudes que se dan en la resolución de
un puzzle o un juego y en la de un genuino problema matemático,
y cómo, efectivamente, muchos de los hábitos adecuados para
la tarea matemática podría no adquirirlos igualmente bien
divirtiéndose con ejemplos escogidos de juegos. La elaboración
de un curso completo de heurística en esta dirección sería
un trabajo bien interesante que requeriría una inmersión
a fondo en la abundante literatura existente a fin de analizar los juegos
más apropiados para cada aspecto y para comprobar el rendimiento
efectivo de esta actividad. Trataré en lo posible aquí de
presentar ejemplos bien conocidos a fin de evitar introducciones quenos
llevarían mucho tiempo.
A.-
Directrices heurísticas basadas en juegos.
COMO RESOLVERLO
1.
ANTES DE HACER TRATARÉ DE ENTENDER. No pienses que es una observación
del todo tonta. La experiencia dice que son muchos los que se lanzan a
hacer cosas a lo loco, por si alguna da en el blanco por casualidad.
¿Sabes bien de qué va?
¿Cómo funciona las diferentes partes del
juego? Estúdialas una a una: forma del tablero, reglas, funcionamiento
de las fichas...
Hazte una o varias figuras si te parece que te va bien.
Juega un poco con las fichas o las partes del juego según
las reglas para familiarizarte con su forma de actuar.
2. TRAMARÉ
UNA ESTRATEGIA. Busca conexiones con otros elementos que conozcas.
Tal vez necesitarás construirte un juego auxiliar más simple
que puedas resolver.
Al final de esta etapa deberías construirte un
plan de ataque concreto.
Aquí tienes algunas observaciones y preguntas
que te pueden ayudar en esta tarea.
Ya me lo sé. ¿Lo has visto antes?
¿Lo has visto en forma parecida al menos?
No me lo sé, pero conozco uno que... ¿Conoces
algún juego semejante, relacionado con éste de alguna manera?
¿Sabes algo del otro que pueda ayudarte en éste?
¿Cómo marchaba aquél? Tienes
un juego semejante en el que sabes cómo actuar. ¿Puedes usar
la misma forma de proceder? ¿Puedes usar la misma idea que conduce
allí a la solución? ¿Deberías introducir en
éste alguna modificación que lo haga más semejante
a aquél?
Empezar por lo fácil hace fácil lo difícil.
¿Puedes resolver al menos parte del juego? ¿Lo puedes hacer
en circunstancias especiales, suponiendo por ejemplo que hubieras conseguido
superar una etapa inicial? Supón que se te pide un poco menos, ¿puedes
entonces?
Supongamos el problema resuelto... ¿Puedes
tratar de recorrerlo hacia atrás? ¿Puedes pensar desde aquí
en alguna pista?
Si hago esto, entonces queda así... A ver si
puedo transformar el juego en otro más sencillo. Introduce tú
mismo modificaciones en las reglas, en las condiciones... tratando de sacar
alguna luz de estas modificaciones.
Me hago un esquema, me lo pinto en colores, me escribo
una ecuación... Procura, por todos los medios a tu alcance tener
un buen esquema de los puntos principales en la mente.
Veamos de nuevo... ¿Para qué son así
las reglas? ¿Cuál es la mala (o buena) idea detrás
de ellas? Fíjate de nuevo en la estructura del juego. Trata
de encontrar pistas en la diferente función de las partes.
3.
MIRARÉ SI MI ESTRATEGIA ME LLEVA AL FINAL. Trata de poner
en práctica tus planes.
Ya tengo una idea. Vamos a ver si marcha. Lleva
adelante tu estrategia con decisión. No te arrugues fácilmente.
Si tienes varias ideas, pruébalas una a una, por orden. No las mezcles
en un principio sin ton ni son.
No nos liemos... Probaré otra cosa. No
te emperres demasiado en una sola estrategia. Si te lleva a una situación
muy complicada, vuelve al paso segundo y busca otra estrategia. Probablemente
hay otro modo más sencillo.
Lo conseguí... ¿Por casualidad?
Si te va bien con tu estrategia, estúdiala detenidamente para convencerte
de que no es por casualidad.
4. SACARÉ
JUGO AL JUEGO. No consideres que ya has terminado del todo cuando lo
has resuelto. Míralo a fondo. Aprovecha tu solución para
asimilar bien la experiencia.
No sólo sé que va, sino que veo por
qué va. Trata de localizar la razón profunda del éxito
de tu estrategia.
Con los ojos cerrados. Mira a ver si con la luz
que ya tienes encuentras otra estrategia, otra solución más
simple.
Ahora veo la astucia de las reglas. Trata de entender,
a la luz de tu solución, qué lugar ocupan las condiciones
y reglas del juego.
Además con esto gano a aquel otro juego.
Mira si otros juegos semejantes funcionan también con el mismo principio
que has encontrado.
Me hago otro juego... y lo patento. Constrúyete
un juego semejante al que has resuelto modificando sus piezas o sus reglas
y mira si tu principio vale aquí también.
##########################
A continuación trataré
de ilustrar algunas de las observaciones anteriores con
juegos concretos.
¿Cómo marchaba aquél?
Un pastor, con una col, una oveja y un lobo (se supone
que hasta cierto punto amaestrado) se encuentra a la orilla de un río
que quiere atravesar. Hay en su orilla una barca en la que cabe él
y una sola de sus pertenencias al tiempo. ¿Cómo se las ingeniará
para pasarlas todas? Si deja solas a un lado oveja y col, ésta será
liquidada rápidamente por la oveja. Si deja oveja y lobo solos a
un lado, el lobo se zampará a la oveja. En cambio al lobo no le
atrae nada la col y bien se puede quedar solo con ella.
El problema es clásico y fácil de resolver
sin grandes esfuerzos sistemáticos. Pero existe una solución
sencilla acudiendo, como sucede en muchas ocasiones en que se trata de
realizar secuencialmente un conjunto de tareas, a la teoría de grafos.
Apuntamos las posibles situaciones de las pertenencias
del pastor en la orilla inicial I sin que le desaparezca nada. Así
A continuación señalamos con una flecha los
posibles pasos de una situación a otra según la regla del
juego, es decir que en la barce sólo pueden cruzar el pastor y una
sola de sus pertenencias. Así se obtiene el grafo que sigue.
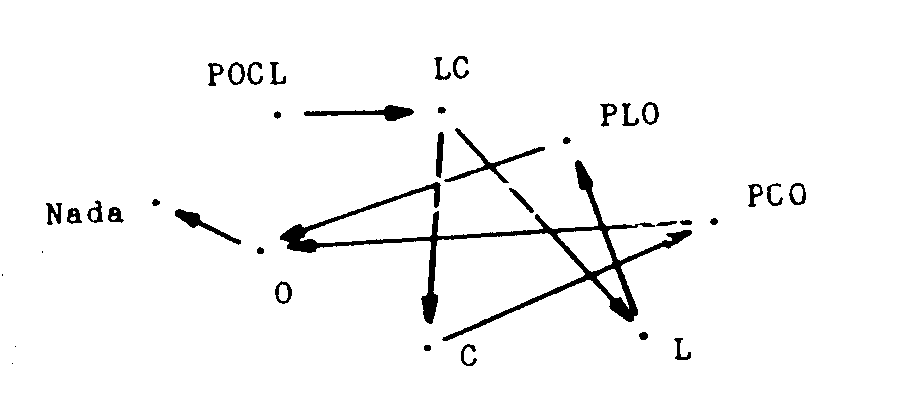Nuestro problema ahora consiste en hallar un camino de flechas
desde POCL hasta Nada. En el cuadro es evidente que hay solamente dos posibilidades
(1) POCL - LC - L - PLO - O - Nada
(2) POCL - LC - C - PCO - O - Nada
La interpretación de las operaciones que el pastor
ha de hacer es clara.
Cualquiera que haya visto esta solución y se enfrente
ahora con el también clásico problema de los dos maridos
celosos, tendrá muy claro cómo debe de proceder. El problema
consiste en resolver la dificultad con que se encuentran dos maridos A,B
que llegan con sus respectivas esposas a, b a la orilla de u río
que quieren cruzar. Hay una barca en la que solo caben dos personas al
tiempo. El problema sería más fácil si no fuera porque
los dos maridos son tan celosos queno pueden sufrir que la esposa esté
ni un momento en compañía de otro hombre sin estar él
delante. ¿Cómo podrán arreglárselas?
Escribimos como antes las distintas situaciones posibles
y unimos con una flecha aquellas que son alcanzables desde otras según
ls reglas.
Así
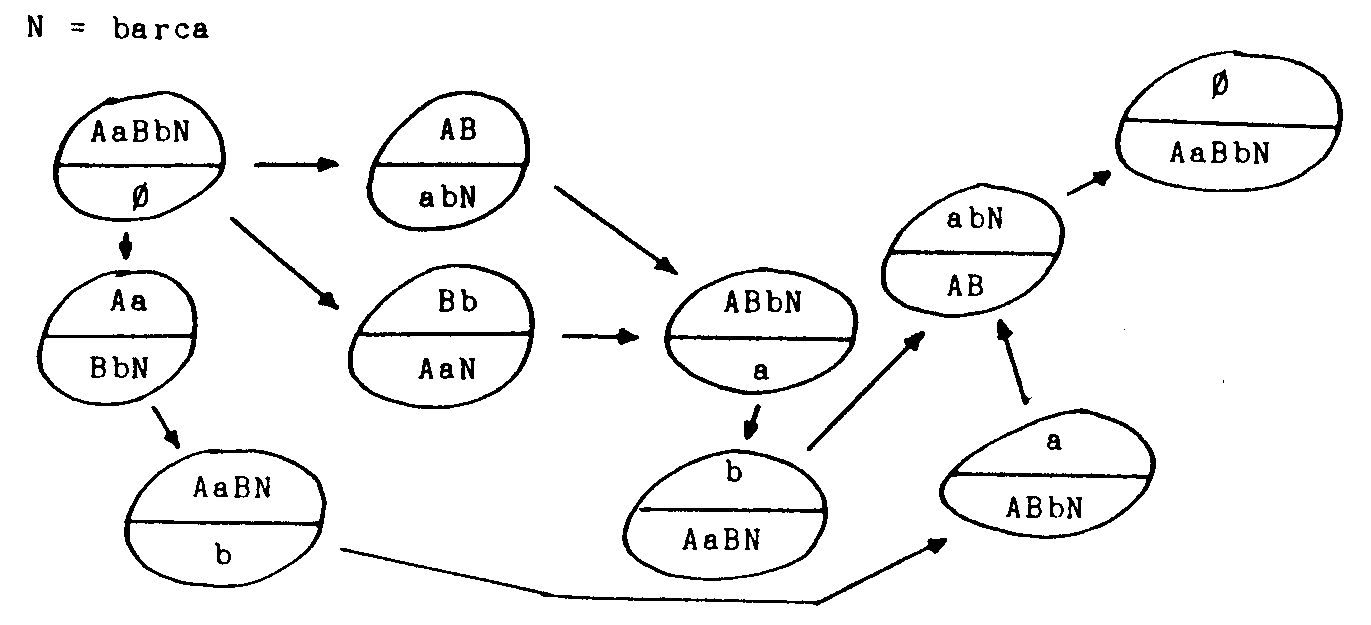De esta forma no sólo podemos encontrar una solución,
sino que podemos obtenerlas todas y escoger la mejor, si es que hay alguna
mejor.
Empezar por lo fácil hace fácil lo difícil.
En un tablero de ajedrez se tapan dos cuadros de los
extremos de una diagonal. Quedan 62 cuadros. Se tienen 31 fichas de dominó
o de papel, cada una capaz de cubrir dos cuadros contiguos. Se pide colocar,
si se puede, las fichas de dominó de modo que cubran exactamente
los 62 cuadros del tablero.
Si empezamos por colocar fichas al buen tuntún,
sin pensar un poco antes, pronto nos encontraremos en un buen lío,
porque aquí se puede efectivamente empezar a hacer cosas sin sistema
y llegar bastante lejos cubriendo el tablero. Pero nuestros intentos sucesivos
van fracasando y aconsejándonos que recapacitemos...
El tablero es grande, hay muchas posibilidades. ¿Y
si nos construímos uno más modesto e intentamos allí
un problema semejante? Tal vez el tablero 2x2, 3x3, 4x4,... En el tablero
2x2 pronto nos damos cuenta de que lo que se pide es imposible sin partir
en dos una ficha. Los dos cuadros que quedan están en una diagonal
y no hay forma de cubrirlos con una ficha de dominó. En el tablero
3x3 el juego no tiene sentido, pues si se cubren 2 cuadros, quedan 7 que
no pueden ser cubiertos ni con tres fichas ni con cuatro exactamente. En
el tablero 4x4 no existe este problema, pero la experiencia del tablero
2x2 nos puede hacer pensar en la imposibilidad aquí también...
¡Sí! En el de 4x4 se quitan dos cuadros de una diagonal, dos
cuadros por tanto del mismo color, como sucedía en el de 2x2. Quedan
8 cuadros de un color y 6 del otro. Pero una ficha de dominó bien
colocada cubre necesariamente un cuadro blanco y otro negro... Así
es imposible cubrir el tablero. Y esto mismo sucede en el caso 8x8, 10x10,..
Además esto va a suceder siempre que quitemos dos cuadros del mismo
color.
Este principio de empezar por lo
fácil es de amplia aplicación. Las dificultades provienen
a menudo de la complejidad de la estructura que nos encubre los rasgos
básicos. Estos quedan muy a menudo más claros en un problema
semejante más sencillo. Descubierto aquí el principio, éste
puede ser aplicado al caso más complicado. La dificultad puede consistir
en encontrar un problema más sencillo que el propuesto que, con
todo, conserve sus rasgos fundamentales.
Otras veces la solución del problema sencillo
es útil, no sólo porque revele un principio que puede ser
utilizado para el problema original, sino porque constituye una parte,
un escalón en el que nos podemos apoyar para resolver el problema
inicial.
En el conocido problema de los 15 se tiene un cuadrado
4x4 en el que se pueden deslizar 15 cuadraditos 1x1 numerados del 1 al
15 utilizando el hueco restante. Se presenta el cuadrado con los números
desordenados.
Se pide colocarlos en orden con el hueco en la esquina
del SE, es decir
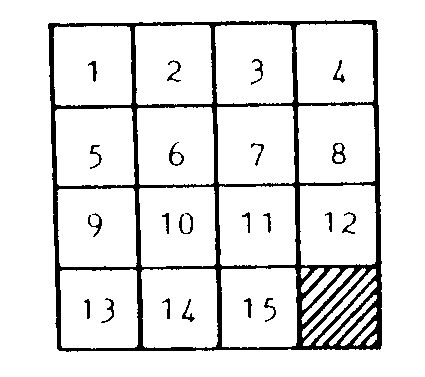
Al acudir a un problema más sencillo, por ejemplo
un cuadrado 2x2 con tres cuadraditos 1x1, se puede uno percatar fácilmente
de que el problema propuesto es a veces insoluble y trivial cuando es soluble.
Si acudimos al problema semejante de un rectángulo 3x2 con cinco
piezas
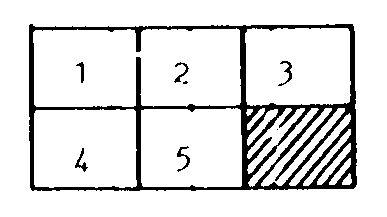
podemos encontrar fácilmente una estrategia para
resolver aquí cualquier problema soluble. Resuelto este problema
ya tenemos una estrategia para el original de los 15, observando que en
tablero de los 15 podemos dejar fijas todas las fichas excepto las de un
rectángulo 3x2 o 2x3 en el que colocamos el hueco y con esta flexibilidad
resolvemos fácilmente cualquier problema soluble. ¿Sabrías
determinar cuáles son los problemas solubles y los insolubles?
Supongamos el problema resuelto.
Se dan las siguiente figuras A y B
¿Puedes trazarlas sin levantar el lápiz
del papel, sin repetir dos líneas y saliendo y terminando en un
mismo vértice?
Las dos figuras se pueden trazar sin levantar el lápiz
del papel, pero A parece resistirse más a un camino que termina
en el punto de partida. ¿Por qué? Supongamos que en A hubiese
tal camino, es decir, supongamos el problema resuelto. Entonces, cada vez
que llegamos a un vértice de paso en nuestro camino (no inicial
ni final), salimos de él por una línea distinta no recorrida
antes. Así cada vértice de paso tiene que tener un número
par de arcos que concurren en él. También en el vértice
de salida tienen que concurrir un número par de arcos, el arco de
salida, el arco de llegada y el número par de arcos correspondientes
a los pasos por él. Como A tiene los dos vértices de abajo
con tres líneas concurrentes en cada una de ellos, el trazado pedido
es imposible.
Me hago un esquema, me lo pinto en colores, me escribo
una ecuación....
Una forma adecuada de representación de un juego
puede dar un método para resolverlo y para resolver al tiempo muchos
otros semejantes.
De entre los problemas clásicos de Bachet, tal
vez los más conocidos son los relativos a medidas. Consideremos
el siguiente: Se tienen junto a una fuente una medida de 7 litros y otra
de 11. Pero nosotros necesitamos medir exactamente dos litros. ¿Cómo?
Existe una representación gráfica muy útil
en los problemas de este tipo.
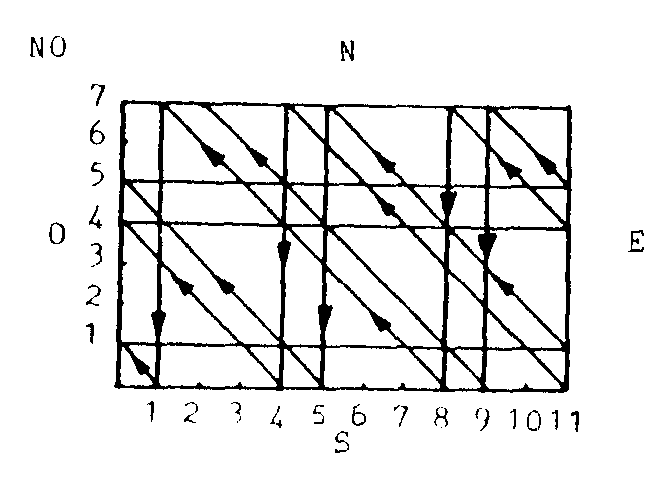
Las coordenadas horizontales indican la situación
del recipiente de 11 litros. Las verticales la situación del de
7 litros. Las flechas horizontales hacia el E indican que se va llenando
el recipiente de 11 litros, las oblicuas hacia el NO indican que del de
11 litros se va trasvasando al de 7 litros. Las flechas verticales hacia
el S indican que el de 7 se vacía de lo que contiene.
La sucesión de operaciones queda bien clara por
el diagrama siguiendo las flechas desde la esquina SE hasta el momento
en que llegamos al otro punto gordo de la figura (el de 11 conteniendo
2 litros):
Se llena el de 11 (punto gordo de salida) y se pasa todo
lo que se puede al de 7 (línea NO). Se vacía el de 7 (linea
hacia S). Se echan los 4 que hay en el de 11 en el de 7 (línea NO).
Se llena el de 11 (línea hacia E). Se trasvasa del de 11 al de 7,
que contenía 4 (línea NO), quedando 8 en el de 11...
Ya hemos visto también cómo los problemas
clásicos sobre cruces pueden tratarse con una gráfica adecuada.
También los problemas sobre pesas admiten un tratamiento semejante.
Veamos de nuevo... ¿Para qué son las
reglas así? ¿Cuál es la mala o buena idea detrás
de ellas?
Escribe, sin que yo lo vea, un número de tres
cibras abc. Repítelas y forma el número de 6 cifras abcabc.
Divídelo por 7. Divide el resultado por abc. Divide el resultado
por 11. Lo que te resulta es 13.
Si alguien te hace el jueguecito y no lo conoces, te
deja un poco perplejo. Para salir de tu sorpresa, sigue la receta de arriba.
El número abcabc se puede dividir por 7, por 11, por 13, es decir
por 7x11x13=1001. Además abcabc es divisible por abc...¿Quién
es abcabc? ¿Qué tiene que ver con el número 1001?...
Fácil: abcabc=abcx1001+abc= abcx1001. Ahora sí que está
clara la cosa. ¿Podrías inventar un juego parecido con el
mismo principio?
Muchos de los puzzles de alambres y cuerdas llevan en
su misma estructura la pista adecuada para dar con la solución.
Por ejemplo el siguiente de las guindas:
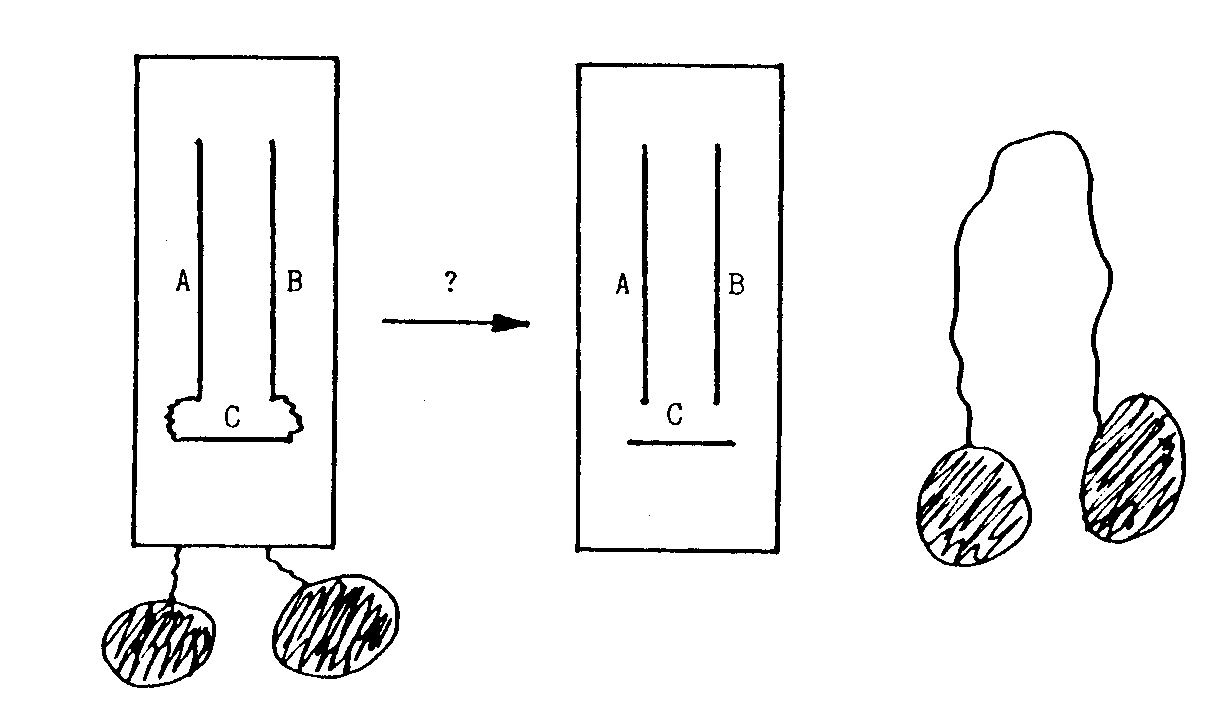
Las dos cuerdas están unidas por una cuerda. El
rectángulo es de papel con los tres cortes indicados A, B, C. Las
guindas son muy grandes para pasar por C sin romper el papel. ¿Cómo
separar las guindas del papel?
No sólo sé que va, sino que veo por
qué va.
El juego de Nim consiste en lo siguiente. Se ponen tres
montones de piedrecillas, uno con 3, otro con 4, otro con 5. Juegan dos
jugadores A y B. El primero en jugar, A, puede quitar tantas piedras como
quiera (siempre una o más) de uno sólo de los tres montones.
Luego juega B del mismo modo. Gana quien se lleve la última piedra.
Tal vez te haya contado alguien la estrategia infalible
que tiene A. Se ponen en sistema binario los números de piedras
de cada montón. Al empezar estos son
3-------------
1 1
4------------- 1 0 0
5------------- 1 0 1
La estrategia consiste en quitar las piedras que haga
falta del montón adecuado para que losunos de cada columna de losnúmeros
en sistema binario sumen un número par. Así, aquí
se pueden quitar dos piedras del montón de 3 y queda
1-------------
1
4------------- 1 0 0
5------------- 1 0 1
El primer jugador gana necesariamente siguiendo esta
misma estrategia cada vez que le toque jugar.
¿Te has parado a pensar alguna vez por qué
marcha? ¿Por qué A puede llevar a cabo su estrategia haga
B lo que haga? ¿Y si los montones tienen números de piedras
diferentes a 3, 4, 5?
Si lo averiguas no te será difícil tal
vez dar con la estrategia del juego de Moore, que es como el de Nim, pero
pudiendo quitar las piedras que se quiera (siempre una o más) de
uno o dos montones en cada turno.
Con los ojos cerrados. Consideremos ahora el juego
siguiente con un montón de 40 piedras. Los jugadores A puede quitar
1,2,3,4, ó 5 piedras a su antojo. Luego B puede quitar así
mismo 1,2,3,4, ó 5 piedras. Ahora le toca a A. Gana quien se lleve
la última.
La estrategia de A consiste en dejar, siempre que no
se pueda llevar todas la piedras que quedn, un número de piedras
que sea multiplo de 6. Es claro que así B no puede ganar, y como
gana alguien seguro, tiene que ser A quien gane. Una vez que A conoce la
estrategia, no le hace falta hacer cuentas más que la primera vez
que juega, en que quita 4 piedras, dejando 36. A partir de entonces su
táctica es sencilla: si B quita m, A quita 6-m.
Y además, con esto gano a aquel otro juego...
En un tablero de ajedrez se señalan dos cuadros
A y B. ¿Es posible pasearse con una torre por todo el tablero comenzando
en A y terminando en B? Recordemos que la torre se mueve horizontal y verticalmente,
nunca en oblicuo.
Por supuesto que uno piensa enseguida en lugar a lo mismo
en un tablero más pequeño, como en el juego del ajedrez recortado
que hemos visto antes y así resulta fácilmente que a veces,
por ejemplo en un tablero 2x2 con A y B en dos esquina diagonalmente opuestas
el paseo propuesto es imposible. Asímismo, quien conozca el uso
que en el otro juego hemos hecho de los colores, puede pensar rápidamente
en aplicar el mismo principio aquí. Si A y B son del mismo color,
blanco por ejemplo, el paseo es imposible en el tablero 8x8. En efecto
la torre va recorriendo sucesivamente blanco, negro, blanco, negro,...
Así si el paseo terminase en blanco, el número de cuadros
sería impar. En cambio será imposible el paseo en un tablero
con un número impar de cuadros si A y B son de distinto color y
también si son del mismo color si es que este color es el m´s
escaso en el tablero. ¿Podrías dar con un teorema general
y una estrategia para hacer el paseo siempre que se pueda?.
B.
Directrices temáticas para el uso de los Juegos.
Me ha parecido de interés elaborar
un segundo esquema de utilización de juegos que, pienso, puede parecer
a muchos más directamente aprovechable. En él trataré
de señalar mediante ejemplos concretos cómo diversos temas
y actitudes quenos ocupan en nuestra enseñanza a todos los niveles
pueden ser motivados, ilustrados y enriquecidos mediante el uso de juegos.
La disposición de este esquema será presentada alrededor
de unas cuantas actitudes y núcleos temáticos propios de
la actividad matemática. El campo es enormemente rico. Pienso que
sería muy útil una experimentación sistemática
y de equipo con estos y otros elementos para averiguar el valor efectivo
de estas ideas a fin de comunicar los temas y actitudes deseadas.
Bajo cada epígrafe concreto
menciono algunos juegos que, en mi opinión, pueden ayudar adecuadamente
a mejor ponerlo de relieve. Ante la imosibilidad de exponer aquí
el juego por extenso he optado por indicar algún lugar, lo más
asequible posible, en la literatura actual donde se puede acudir para obtener
información detallada. La mayor parte de las referencias que doy
se encuentran en los libros de Martin Gardner. Este ha publicado hasta
el presente ocho antologías de las mejores de sus contribuciones
en Scientific American. Estas antologías serán citadas
de la forma Gardner 1, Gardner 6, etc. Y en la bibliografía presentada
en la tercera parte de mi trabajo se puede ver el título y referencia
exacta. De las antologías de Gardner han sido traducidas al castellano,
en Alianza Editorial, 3, 4, 7, 8, y también han sido publicados
en castellano por Labor los dos libros suyos "Inspiración. ¡Ajá!
Paradojas". Las otras referencias que daré, serán indicadas
por completo en el lugar en que aparecen, o se pueden localizar fácilmente
en la bibliografía que presento en la tercera parte.
1. SORPRESAS
MATEMÁTICAS.
"Por la admiración comenzó
el hombre a filosofar", dijo Aristóteles, y la admiración
y la sorpresa y la curiosidad siguen contándose entre los elementos
motivadores más fuertes de nuestra actividad intelectual. Cualquiera
denosotros que explore un poco en el origen de nuestro interés por
las matemáticas encontrará sin duda instantes de sorpresa
y admiración ante ciertos hechos matemáticos que nos han
llamado poderosamente la atención. Los hay a todos los niveles,
elementales, menos elementales, simples, más sofisticados,... En
la enseñanza la motivación es el motor esencial. ¿Por
qué no apoyarnos en los elementos más adecuados para ponerlo
en marcha con energía? Incluso cuando se trata de hechos que no
pueden ser explicados plenamente, estos pueden presentar aspectos de misterio
que motiva fuertemente el interés por saber más para desvelarlo
plenamente.
Dentro de lo que constituye el contenido
matemático propiamente dicho, existen multitud de hechos con carácter
de sorpresa. He aquí algunos:
1.1. Las tres mediatrices de los lados de un triángulo
concurren; las tres alturas también; las tres bisectrices también.
1.2. Teorema de Desargues; teorema del hexagrama místico
de Pascal (Guzman, Mirar y Ver, Cap.7).
1.3. Teorema de Steiner: Se dan dos círculos E,
I, uno, I, interior al otro, E. Se traza un círculo C1,
tangente a los dos, luego otro C2,
tangente a C1, E,
I, luego otro C3,
tangente a C2, E,
I, y así hasta Cn,
tangente a Cn-1, E,
I. Supongamos que al hacerlo resulta además que Cn
es tangente a C1*,
obtenemos asímismo una cadena C1*,C2*,...,
Cn* tangente a C1*.
(La demostración resulta fácil mediante una inversión
que transforme E, I, en círculos concéntricos).
1.4. Teorema de Poncelet: Se dan dos círculos
E, I, con I interior a E. Se traza una secante S0,S1
en E que sea tagente a I, luego otra distinta S1S2
asímismo tangente a I,... hasta obtener Sn-1Sn.
Supongamos que Sn coincide son S0.
Entonces si repetimos la operación con otro S0*
inicial, obtenemos una cadena de secantes S0*S1*,S1*S2*,...,
Sn-1*Sn*,
y resulta también que Sn*
coincide con S0*.
(Apesar de la semejanza con el teorema de Steiner, el modo de demostración
es distinto. Este es un hecho importante en la historia de la geometría
algebraica) (Schoenberg I.J., Mathematical Time Exposures, The Mathematical
Association of America, Washington D.C., 1982; Cap.14).
1.5. Si tres círculos del plano son tangentes
dos a dos, existe un cuarto círculo tangente a los tres (Fácil
por inversión).
1.6. El collar de las seis perlas. Se tienen tres esferas
tangentes dos a dos exteriormente. Se comienza a ponerles un collar de
perlas eféricas de distinto tamaño en general del siguiente
modo. Primero se traza una esfera cualquiera E1
tangente exteriormente a las tres (hay muchas). Luego trazamos otra
E2 tangente exteriormente
a las tres y a E1(sólo
hay una). Continuamos con otra E3
tangente a las tres y a E2.
Etc... Entonces, sea cual sea E1,
siempre este collar se cierra con E6
tangente a E1 (Demostración
fácil por inversión).
1.7. Hay infinitos números primos.
1.8. Proceso diagonal de Cantor. El conjunto de palabras
infinitas de dos letras no es numerable. El conjunto de los números
reales no es numerable.
1.9. Es posible hacer una partición de un cuadrado
en cuadrados desiguales más pequeños (Gardner 2, Cap. 17).
En cambio es imposible hacer una partición de un cubo en un número
finito de cubos desiguales más pequeños (Gardner 6, Cap.
21).
2. CUENTOS
CON CUENTAS.
Existen constelaciones de hechos matemáticos
que se prestan para hacer de ellos una novela bien interesante. Me pregunto
si el tiempo malgastado en muchos de nuestros rollos magistrales en los
que tanto abundamos los profesores de matemáticas de todos los niveles
no podría invertirse con gran provecho en contar pausadamente alguna
de estas historias apasionantes del pensamiento humano. He aquí
algunos temas:
2.1. El ábaco (Gardner 4, Cap.18).
2.2. Sección áurea, sucesión de
Fibonacci, etc...(Gardner 4, Cap. 13);(Gardner 2, Cap.8).
2.3. Triangulo de Pascal (Gardner 7, Cap.15).
2.4. El número Pi (Gardner 3, Cap. 8).
2.5. El teorema de los cuatro colores (Guzmán,
Cuentos con Cuentas; Gardner 3, Cap.10).
2.6. Propiedades de la elipse (Guzmán, Cuentos
con cuentas).
2.7. Hélice (Gardner 6, Cap.1).
2.8. Grafos (Gardner 6, Cap. 10; Ore, O. Graphs and their
Uses, NML the Mathematical Association of America, Washington D.C., 1963).
2.9. Cicloide (Gardner 6, Cap. 13).
2.10. Propiedades del retículo de enteros (Guzmán,
Mirar y Ver, Cap.1).
2.11. Convexos, teorema de Helly, Minkowski,...(Guzmán,
Mirar y Ver, Cap 3,4,5).
2.12. Teorema del punto fijo y aplicaciones (Guzmán,
Mirar y Ver, Cap. 8, 9).
2.13. Banda de Möbius (Gardner 8, Cap. 8; Gardner
1, Cap 7).
3.
SISTEMAS DE NUMERACIÓN.
Existen muchos juegos cuya base o
cuya estrategia se encuentra en una adecuada utilización de diferentes
sistemas de numeración.
3.1. Nim (Guzman, Cuentos con Cuentas).
3.2. Averiguar un número mediante tarjetas basadas
en el sistema binario (Gardner3, Cap. 1; Guzmán, Nuestra Escuela,
Octubre 1984).
3.3. Las torres de Hanoi y el juego icosiano (Gardner
1, Cap. 6).
3.4. Uso del sistema ternario en juegos (Gardner 6, Cap.
11).
4.
CRITERIOS DE DIVISIBILIDAD.
Los libros clásicos de Rouse
Ball, Dudeney, Schuh, Kraitchik,... contiene muchos juegos basados en diferentes
propiedades aritméticas.
4.1. Escribe un número cualquiera. Multiplicalo
por 9. Tacha una cifra cualquiera distinta de 0. Dime lo que suman las
restantes y yo te diré qué cifra es la tachada. (Fácil:
Criterio de divisibilidad por 9).
4.2. El computador me ha escrito 15! por extenso, pero
hay una cifra que no puedo leer. ¿Puedes decirme cómo averiguar
rápidamente cuál es?. (Fácil: Divisibilidad por 9
y por 11).
4.3. Averigua una estrategia par el siguiente juego.
Dos jugadores A y B con un montón de piedrecillas. Juega A quitando
1 y 6. Juega B quitando de las que quedan entre 1 y 6,... Gana quien se
lleva la última. (Otro juego: gana quien no se lleva la última)(La
estrategia para el primer juego es dejar un número de piedras múltiplo
de 7).
4.4. Escribe un número de tres cifras abc. Repítelas
para formar uno de 6 abcabc. Divide por 7, divide lo que queda por abc,
divide por 11. Te resulta 13.
5. INDUCCION.
5.1. Torres de Hanoi. ¿Cuál es el número
mínimo de movimientos? (Gardner 1, Cap.6).
5.2. Teorema de Euler C+V=A+2 (Guzmán, Cuentos
con Cuentas).
5.3. Los puentes de Köngsberg (Guzmán, Mirar
y Ver; Guzman, Cuentos con Cuentas).
5.4. Lema de Sperner (Guzmán, Mirar y Ver, Cap.7).
5.5. Falsa inducción: Rana Saltarina (Guzmán,
Cuentos con Cuentas).
6. CONTAR
SIN CONTAR.
Una gran porción de la matemática
se reduce a encontrar trucos para obtener información cuantitativa
de una situación dada de la forma más sencilla posible. Hay
unos cuantos de ellos que, a pesar de su aparente trivialidad conducen
a resultados verdaderamente profundos.
6.1. Principio de Dirichlet: Un palomar tiene 16 agujeros.
Una bandada de 17 palomas se cuela en él. ¿Puedes sacar alguna
conclusión interesante?
6.2. En cualquier momento dado hay en Madrid más
de 20 personas con exactamente el mismo número de pelos en su cabellera
(Hazte un palomar con 150.000 agujeros, número de pelos que como
mucho soporta un mortal en su cabeza, y vete metiendo a cada madrileño
en el agujero correspondiente a su número de pelos).
6.3. Teorema de Ramsey (versión sencilla): Se
señalan 6 puntos sobre una circunferencia. Se trazan todos los segmentos
que unen cada par de ellos. Se colorean de rojo o verde. Entonces, lo hagas
como lo hagas, te encontrarás con que algún triángulo
de los formados por estos segmentos tiene los tres lados del mismo color
(Guzman, Contar, Nuestra Escuela, octrubre 1984).
6.4. Juegos de cartas con un principio aritmético
(Guzmán, Contar, Nuestra Escuela, Octubre 1984; Gardner 1, Cap.
10).
6.5. Un truco topológico. Pinta un circuito cerrado
con cruces todo lo complicado que quieras, como este, sin que yo lo vea.
Que no haya cruces triples, cuádruples,...
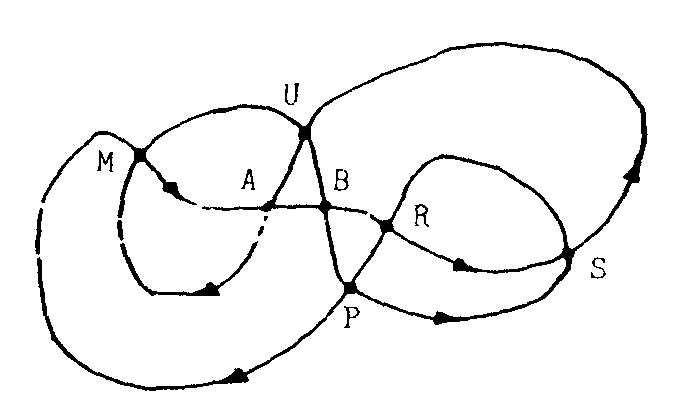
Pon a cada punto de cruce una letra a tu antojo. Ahora
recorre el circuito y vas diciéndome las letras. Cuando tú
quieras cambias una vez las letras sucesivas para engañarme. Por
ejemplo, en el de arriba me dices
MARBSUAMUBPSRP
y te adivino cuál es el cambiazo que me has dado
(Me basta escribir las otras a medida que me las das una ariba y otra abajo
de una raya, así
MRSAUPR
ABUMBSP
al observar que cada una está una vez arriba y
otra abajo excepto las cambiadas R y B. Has cambiado B por R) (Gardner
3, Cap. 9).
6.6. La historia del pequeño Gauss. El maestro
manda a su clase hallar la suma de los 100 primeros números. Quería
tranquilidad para un rato largo. Gauss escribe inmediatamente algo así
S = 1
+ 2 + 3 + .............................+
98 + 99 + 100
S = 100 + 99
+ 98 + .............................+ 3 +
2 + 1
2S= 101 + 101 + 101+ ..............................+
101+101+101 = S 50x101 = 5050
7. DEDUCCION
LOGICA.
El esqueleto de las matemáticas
está compuesto por unos cuantos axiomas que se manipulan mediante
el mecanismo raciocinante del hombre. Está bien que se sepa y que
se ejerciten nuestros alumnos en la deducción, pero tratando al
mismo tiempo de estimular los otros muchos aspectos de la matemática,
intuición espacial, intuición numérica, imaginación,
fantasía, actividad aventurera,...
7.1. ¿Podrías construirte un cuadrado mágico
2x2? ¿Uno 3x3? Busca estrategias para construir cuadrados mágicos
(Garner 1, Cap. 2; Rouse Ball, Cap. 7).
7.2. Diseña una estrategia para jugar bien al
Tres en Raya.
7.3. Un monje budista sale de su templo a las 5´30
de la mañana por una vereda hacia la cumbre de una montaña,
donde llega por la tarde. Allí se queda durante toda la noche y
a las 5´30 del día siguiente inicia el descenso por la misma
vereda. Trata de demostrar que en el descenso ha estado en algún
mismo punto del camino exactamente a la misma hora que el día anterior
(Gardner 3, Cap. 20, Prob.4).
7.4. Toma dos alambres de la misma longitud, rectos.
Uno lo pliegas como y cuantas veces quieras. Lo colocas luego doblado sobre
el otro de modo queno sobresalga. Entonces, lo hagas como lo hagas hay
un punto del alambre doblado que está donde estaba antes de empezar
a plegar (Usa el teorema de Bolzano que dice esencialmente que si quieres
cruzar un río y no tienes ni puente ni barca, tendrás que
mojarte).
8. ELEMENTAL,
QUERIDO WATSON.
He aquí algunos problemitas
elementales que pueden servir para ejercitar el arte de resolver problemas
de acuerdo con las normas heurísticas dadas anteriormente.
8.1. Sin trigonometría, sólo con geometría
elemental, demostrar que en la figura
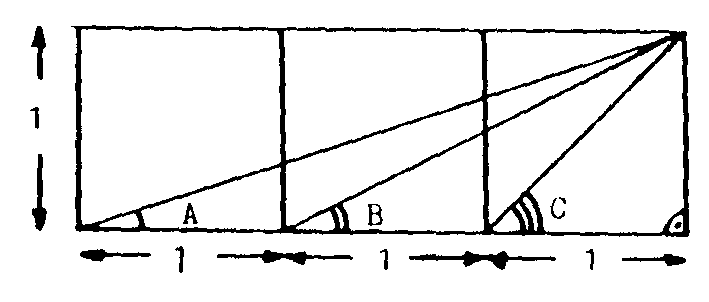
se tiene C=A+B
Solución: Observa con atención la figura
siguiente
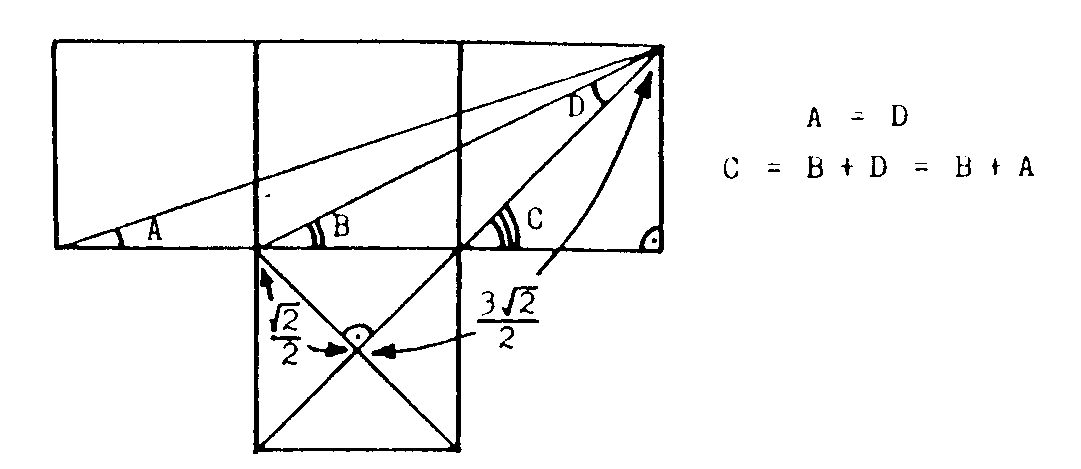
8.2 Las dos rectas señaladas en la figura de abajo
cortan al cuadrado en tres partes de igual área. ¿Cómo
cortan a los lados? Sin hacer cuentas.
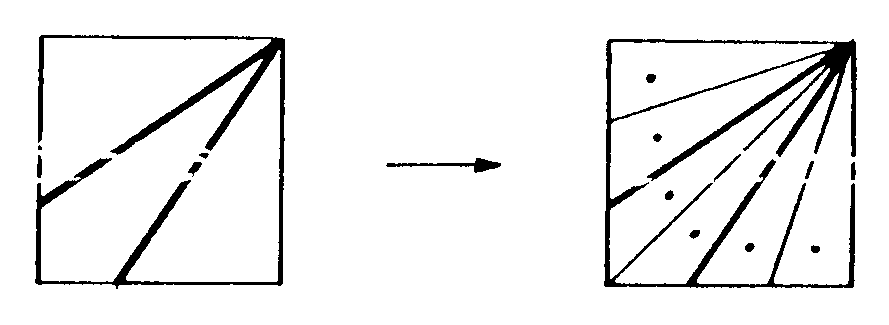
Basta observar la figura auxiliar siguiente con los segmentos
adicionales que se han trazado dividiendo las áreas señaladas
en dos partes iguales. Con ello es claro que las rectas originales van
a parar a 1/3 del vértice opuesto.
8.3. En el interior de un círculo se da un millón
de puntos. Demostrar que existe una recta que deja 500.000 puntos a cada
lado. (Gardner 7, Cap, Prob.8).
8.4. Teoremas geométricos obtenidos cortando y
doblando papel (Gardner 3, Cap.5; Donovan J., Matemáticas más
fáciles con manualidades de papel, Distein, Madrid, 1975).
8.5. Tres Círculos del mismo radio R pasan por
un punto. Demostrar que los otros tres puntos de intersección de
los círculos determinan otro círculo del mismo radio R. (Polya,
Mathematical Discovery, Wiley, New York, 1962).
9. SIMETRIA.
La utilización de la simetría
es técnica muy frecuente en matemáticas... y en juegos. He
aquí algunos ejemplos.
9.1. En el juego de Hex se puede demostrar que el segundo
jugador no puede tener una estrategia para ganar (Gardner 1, Cap. 8).
9.2. Consideramos el siguiente juego para dos jugadores
A y B, en el tablero de ajedrez con 32 rectángulos de papel, cada
uno capaz de cubrir dos cuadros del tablero. Juega A colocando un rectángulo
donde quiera, cubriendo dos cuadrados. Luego juega B cubriendo otros dos
cuadros no cubiertos. Luego A... Pierde el primero que no pueda colocar
un rectángulo que cubra dos cuadros. ¿Sabrías dar
con una estrategia pra alguno de los dos jugadores que le permita ganar
siempre? (Fácil: Simetría) ¿Cómo cambian las
cosas si juegan en un tablero 8x7,..?
9.3. Para construir cuadrados mágicos impares
hay una técnica muy sencilla y fácilmente memorizable. Se
amplía el cuadro, p.e. 5x5, como se indica en la figura, con las
pirámides que he señalado
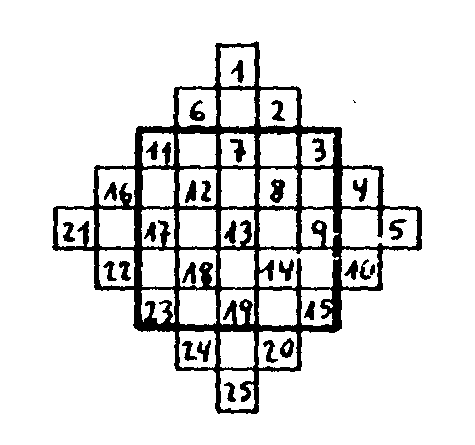
A continuación se colocan los números oblicuamente,
como lo he hecho arriba. Luego la pirámide superior se desliza hasta
abajo del cuadro donde encaja perfectamente. Análogamente se procede
con las otras pirámides. Así se obtiene un cuadro mágico
5x5
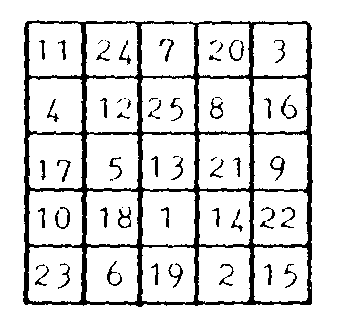
¿Sabrias demostrar por qué sale siempre
bien? (Estudia la simetría de la disposición inicial y a
dónde va a parar cada número después).
9.4. Se considera la siguiente figura
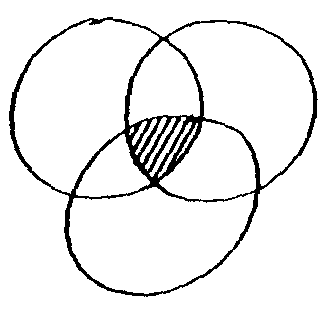
Los tres círculos tienen el mismo radio y cada
uno pasa por el centro de los otros dos. ¿Podrías determinar
si la zona rayada mide más o menos que 1/4 del área del círculo?
Sin cálculos. (Gardner 4, Cap. 15, Prob. 4).
9.5. En un billar ¿cómo llegar con una
bola a otra sin efectos después de dos reflexiones sobre dos bandas?
(Se halla el simétrico del punto de destino con respecto a la última
banda, luego el simétrico de este punto con respecto a la primera
banda que hay que tocar y este punto se une con el de partida, determinando
así el comienzo de la trayectoria).
9.6. El problema de la araña y la mosca. Una araña
en el interior de un vaso cilíndrico quiere llegar lo más
rápidamente posible a una apetitosa mosca que está en el
interior del vaso. ¿Le puedes indicar el recorrido que debe seguir?
(Desenrrolla el cilindro y lo tendrás casi resuelto). ¿ Y
si sustituimos el vaso cilíndrico por una caja de zapatos? ¿Cómo
resuelves ahora el mismo problema?.
9.7. ¿Cómo construir el triángulo
de perímetro mínimo inscrito en un triangulo dado con un
vértice en cada lado de él? (Guzman, Mirar y Ver, Cap. 7).
10. HAZTE
UN DIBUJO.
Un dibujo, un esquema, algún
tipo de representación adecuada, pueden ayudar extraordinariamente
a aclarar las cosas, permitiendo ver mejor los rasgos esenciales, tener
los datos pertinentes a mano, etc... Por eso es natural que los grafos
sean un instrumento utilísimo en tantos juegos y problemas, tanto
de la matemática como de la vida real. Ya hemos visto el uso de
algunos en la sección heurística. He aquí alguno más.
10.1. Las veintiocho fichas de dominó se pueden
colocar en hilera de acuerdo con las reglas del juego... ¡Faltaría
más! ¿Puedes hacerlo si quitas las 7 fichas que tienen seis
puntos? (Gardner 4, Cap. 12).
10.2. Solucción del puzzle de los 4 cubos de colores
"Locura Instantánea" (Berlekamp y otros, Winning Ways vol. 2., p.
784).
10.3. Diversos juegos con grafos. (Gardner 6, Cap. 10;
Ore, 0., Graphs ..their Uses, The Mathematical Association of America,
Washington D.C. 1963).
11.
UTILIZACIÓN DE COLORES.
11.1. Ajedrez recortado (ya citado antes) (Guzmán,
Cuentos con Cuentas).
11.2. Paseos con las torres comenzando en un cierto cuadro
y terminando en otro prefijado. (Ver esquema heurístico).
11.3. Imposibilidad de un paseo hamiltoniano por los
vértices del rombo dodecaedro. (Se colorean los vértices
de la malla plana equivalente a la malla de vértices del rombododecaedro).
11.4. Paseo del caballo por el tablero de ajedrez, un
problema famoso que ocupó, entre otros a Euler. (Gardner 8, Cap.
13).
11.5. Un cubo de madera 3x3 está dividido en 27
cubitos 1x1 de la forma natural. Una termita desea penetrar hasta el cubito
central después de horadar todos los demás cubitos desde
el exterior, comenzando por el centro de alguna cara exterior de un cubito
ymoviéndose paralelamente a los ejes del cubo grande, pasando siempre
de un cubito a otro a través del centro de una cara común.
¿Lo podrá hacer? ¿Cómo? (Gardner 3, Cap. 12,
Prob 9).
11.6. En el tablero siguiente
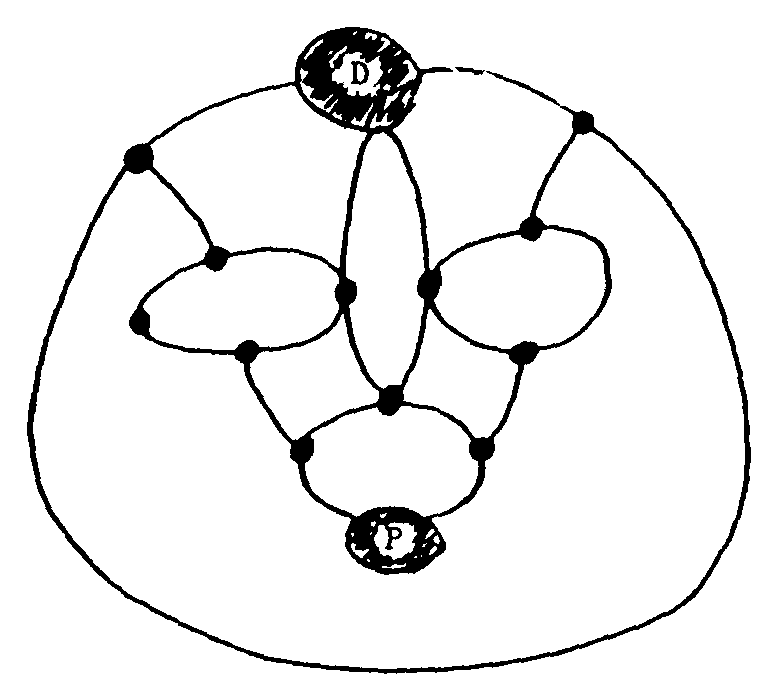
juegan D y P. El jugador D juega con un duro que sale
de D y el jugador P con una peseta que sale de P. Los jugadores s emueven
alternativamente por las rutas señaladas, empezando C. El jugador
D trata de cazar a P y gana si lo consigue en 6 o menos turnos. Si no lo
ha conseguido despues de 6 turnos, pierde. (Gardner 6, Cap. 19, Prob. 3).
12.
COMENZAR POR LO FACIL AYUDA A RESOLVER LO DIFICIL.
Este es un principio importante en
heurística que ya hemos tratado antes y que fácilmente se
olvida. Además de los ejemplos que vimos en el primer esquema, mencionaré
aquí rápidamente algunos más.
12.1. Puentes de Königsberg (Guzmán, Cuentos
con Cuentas).
12.2. Rana Saltarina (Guzmán, Cuentos con Cuentas).
12.3. El ejemplo de 10.1. sobre el dominó es también
utilizable en este contexto. Comienza con un dominó con fichas que
solo tengan, por ejemplo 0, 1, 2, 3 puntos en sus caras.
13.
PIENSA AL REVES. SUPONGAMOS EL PROBLEMA RESUELTO.
Otro principio heurístico del
que ya hemos visto antes algún ejemplo.
13.1. El reparto de cartas interrumpido (Gardner 8, Cap.
14. Prob. 1).
13.2. ¿Qué situación es más
verosímil después de repartir las cartas en el bridge: que
entre tú y tu compañero tengais todos los tréboles
o que entre tú y él no tengais ninguno? (Gardner 8, Cap.
9, Prob. 25).
14.
SOLITARIOS MATEMATICOS.
Existen muchos solitarios con un claro
contenido matemático. Periódicamente, como cometas, salen
de nuevo a la popularidad viejos solitarios inventados hace siglos. De
vez en cuando, como en nuestros días el cubo de Rubik, alguno acapara
totalmente la atención, los matemáticos escriben unos cuantos
artículos sobre él y sus variaciones y luego vuelve a dormirse
en una discreta penumbra. Los solitarios tienen aplicaciones pedagógicas,
por supuesto, pero también las tienen psicoterapéuticas y
no está mal que los profesores de matemáticas nos aprovechemos
de unas y otras tanto para nosotros mismos como para nuestros alumnos.
He aquí unos cuantos solitarios curiosos. Prácticamente todos
los solitarios tradicionales tratables matemáticamente y otros muchos
de reciente invención son discudos en: Berlekamp y otros, Winning
Ways.
14.1. Tangram. Probablemente el más antiguo de
este tipo de solitarios (Gardner 2, Cap. 18; Tangram, Labor, Barcelona,
1981).
14.2. El solitario de la Bastilla. Enormemente popular
desde el siglo 17 (Guzmán, Cuentos con Cuentas).
14.3. El Juego de los 15, de Sam Loyd, que hizo furor
a principios de nuestro siglo y que ya hemos estudiado en parte antes (Gardner
6, Cap. 7 junto con otros puzzles famosos).
14.4. Locura Instantánea (Gardner 3, Cap. 16;
Gardner 8, Cap. 15; Berlecamp y otros, Winnig Ways, vol. 2, p. 784).
14.5. Soma, el solitario famoso de Piet Hein (Gardner
2, Cap.6).
14.6. Poliomino (Gardner 1, Cap. 13; Garner 3, Cap. 13;
Berlekamp y otros, Winning Ways, Cap.24).
14.7. El cubo de Rubik tiene mucha matemática
en sus aristas, pero no se presta mucho a un tratamiento elemental. Una
solución asequible en tres páginas bien claras puede verse
en : Berlekamp y otros, Winning Ways, vol. 2, p. 764-766).
14.8. El juego de la vida, adecuado para explotar el
comportamiento de autómatas autorreproductores (Berlekamp y otros,
Winning Ways, Cap. 25).
15.
PARTIDOS MATEMÁTICOS.
A lo largo de lo ya expuesto hemos
tenido ocasión de ver algunos juegos interesantes para dos jugadores,
como el Nim, el Hex,... Los juegos tradicionales con sabor matemático
abundan y se van creando muchos nuevos de gran interés, basados
en principios nuevos. Pienso que el tratamiento más completo de
juegos matemáticos se puede encontrar en la reciente obra de Berlekamp,
Conway y Guy, Winning Ways, que ya he citado varias veces. He entresacado
aquí algunos de ellos indicando también alguna otra referencia
más asequible.
15.1. Tres en Raya (Gardner 1, Cap. 4).
15.2. Nim y variaciones (Guzmán, Cuentos y Cuentas;
Gardner 1, Cap. 15).
15.3. Ceros y Cruces, el clásico juego sobre una
cuadrícula completando cuadros (Berlekamp y otros, Winning Ways,
Cap. 16).
15.4. Go, un antiguo juego oriental de reglas muy sencillas
y de gran riqueza estratégica. Durante algún tiempo fue asignatura
obligatoria en las academias de preparación militar en Japón.
(Berlekamp y otros, Cap. 19). Es interesante sber que, como en el ajedrez,
no se conoce estrategia completa.
15.5. Otelo, también llamado Reversi, otro juego
de reglas muy sencillas sin estrategia matemática conocida. (Gardner
3, Cap. 6).
15.6. Juegos topológicos: Gale, Bridgit...(Gardner
3, Cap. 19; Gardner1, Cap. 7).
15.7. Hex (Gardner 1, Cap.8).
15.8. El juego militar, un clásico juego de acorralamiento
parecido al de los gatos y el ratón sobre un tablero como el de
abajo (Gardner 6, Cap. 5, donde se pueden encontrar otros juegos de tablero
con estrategia.
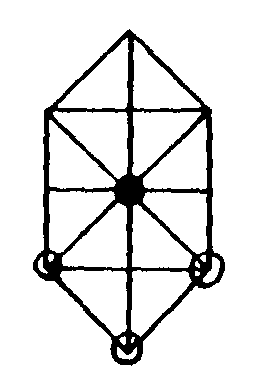
16.
ANALOGÍAS ESCONDIDAS.
Como sucede enmatemáticas,
existen a veces analogías insospechadas en los juegos que uno se
puede proponer, a veces incluso isomorfismos de estructura que permiten
analizar varios de un golpe. Ya hemos visto cómo algunos juegos
y puzzles se convierten, mediante un esquema, en un problema equivalente
de teoría de grafos. He aquí algún ejemplo más
de juegos isomorfos.
16.1. El juego de Moser y el Tres en Raya (Gardner 7,
Cap. 16).
16.2. Juego de cartas equivalente al cuadrado mágico
3x3 (Gardner 7, Cap. 16).
16.3. El juego icosiano y las torres de Hanoi (Gardner
1, Cap. 6).
16.4. Problemas de medidas y de reflexión en un
billar (Gardner 6, Cap 4).
17. FALACIAS.
Las falacias tienen un gran valor
pedagógico. Euclides escribió un libro de falacias y aporías,
los Pseudaria, que probablemente utilizó con gran provecho en su
enseñanza. Los clásicos en recreaciones matemáticas
suelen tener una sección dedicada a falacias. Especialmente recomendables
son las secciones de los capítulos 2 y 3 de Rouse Ball, dedicadas
a falacias aritméticas y geométricas.
17.1. Diversas falacias aritméticas, topológicas,...
(Gardner 1. Cap. 14)
17.2. La siguiente falacia es muy antigua (Torricelli?)
y viene a demostrar que el principio de Cavalieri (mal interpretado) es
falso. Consideramos los dos triángulos de la figura, ABC y ABD,
con BC=BD. Para cada de AB es claro que MN=MP. Así por el principio
de Cavalieri, el área de ABC es igual al de ABD.
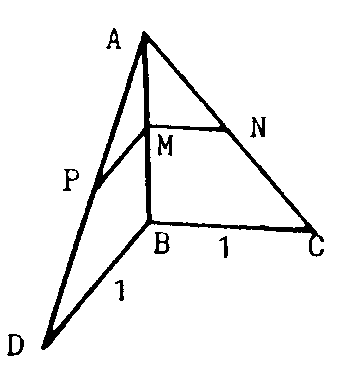18. FELIZ IDEA.
En la resolución de juegos
y acertijos, como en la resolución de problemas, a veces es preciso
que surja en nuestra mente lo que llamamos una feliz idea. Un concepto
nada fácil de definir. Para el experto es un método de trabajo
lo que para el novicio resulta una feliz idea, una especie de revelación
divina que surge como un relámpago en la oscuridad y nos deja ver
claro el camino a seguir. El examen de muchas felices ideas puede abrir
en nuestro espíritu cauces que hagan surgir chispas semejantes en
circunstancias parecidas. Por eso no es nada despreciable esta labor preparatoria.
Con este espíritu está escrito el estimulante y agradable
libro de Martin Gardner "Inspiración, ¡Ajá! ", que
constituye toda una antología de felices ideas en diferentes campos.
3. ALGUNAS INDICACIONES BIBLIOGRÁFICAS.
(Las referencias incluídas a continuación se leerán
más claramente haciendo clic con el botón derecho del ratón
en la región de abajo para obtener la imagen que las contiene aumentadas
en otra página)
A continuación me ha parecido bien
indicar algunos libros que existen en castellano más o menos útiles
para la finalidad qeu he pretendido con este trabajo. Una bibliografía
general más extensa, orientada no exclusivamente hacia losjuegos
matemáticos, sino hacia obras adecuadas para proporcionar motivación
y enriquecimiento histórico, estético y lúdico de
la enseñanza fue confeccionada por mi y distribuida por el ICE de
la Universidad Autónoma de Madrid en 1983 a raíz de un cursillo
sobre juegos matemáticos.
