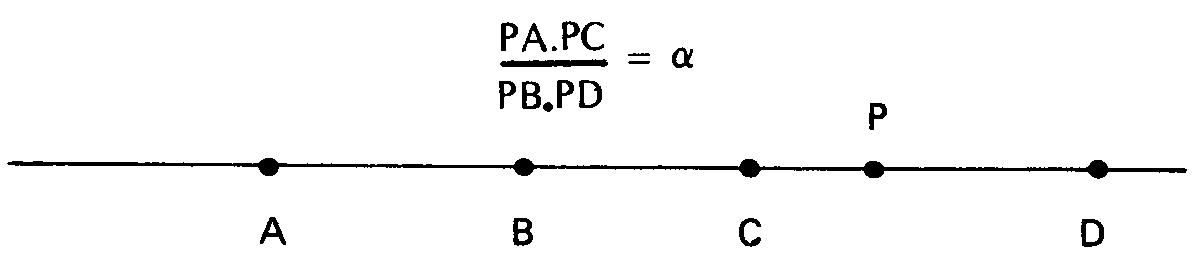Otras obras de Apolonio.
Apolonio escribió unas cuantas
obras más que se difundieron bastante en su entorno, una buena parte
relativa a geometría, otras a campos de la física donde sus
profundos conocimientos geométricos más pudieron aportar,
como es el caso del estudio de la reflexión sobre espejos curvos,
otras de astronomía, campo este en el que Apolonio ejerció
una notable influencia, viniendo citado explícitamente por Tolomeo,
autor del Almagesto (ca.140 d.de C.) como responsable de un importante
teorema en la teoría de epiciclos. Pero parece cierto que las otras
obras matemáticas de las que nos han llegado noticias fueron de
interés más bien puntual, a juzgar por el tipo de problemas
que trataban. He aquí una descripción sucinta de cada una
de ellas.
La única obra, aparte de las
Cónicas, que ha sobrevivido hasta nosotros, tiene por título
Sobre la sección de la razón (logou
apotomh) que fue conservada en árabe y traducida por Halley
al latín en 1706. Halley había hecho el esfuerzo de aprender
árabe a fin de ser capaz de leer esta obra de Apolonio. El problema
principal se puede indicar de la forma siguiente
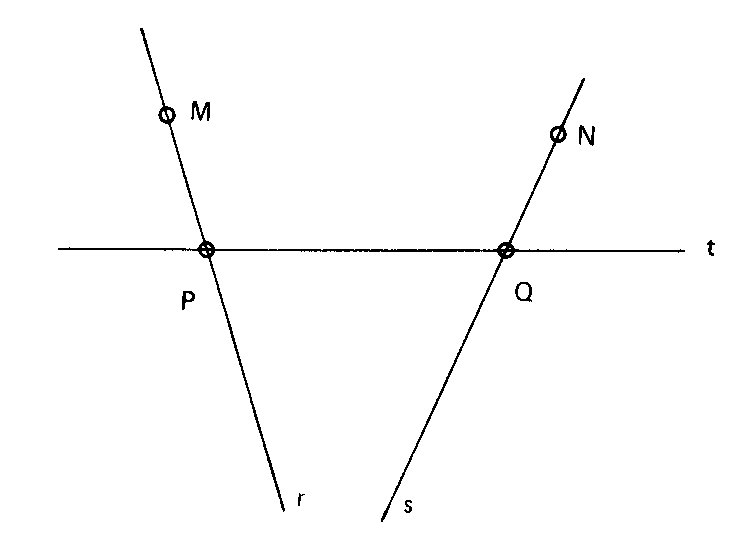Dado el punto A, los puntos M,N, las dos rectas r y s que
pasan respectivamente por M y N y dado el número a
trazar por A una recta T tal que PM/PQ=a
Es fácil para nosotros, mediante
nuestra geometría analítica, ver cómo el problema
se puede reducir a uno acerca de intersección de cónicas
y así es sencillo imaginar cómo pudo proceder Apolonio en
este y otros problemas semejantes con suma facilidad, gracias a sus conocimientos
sobre cónicas.
Otra obra, ésta perdida, se
titula Sobre la sección del área ( cwriou
apotomh ). El problema tratado era como el anterior, salvo que ahora
debería ser MP.NQ=a .
El tratado sobre la Sección
determinada (dcwriomhuh tomh) consistía
en lo siguiente. Dados cuatro puntos sobre la recta A,B,C,D, y el número
a, determinar otro punto P sobre la misma recta
tal que
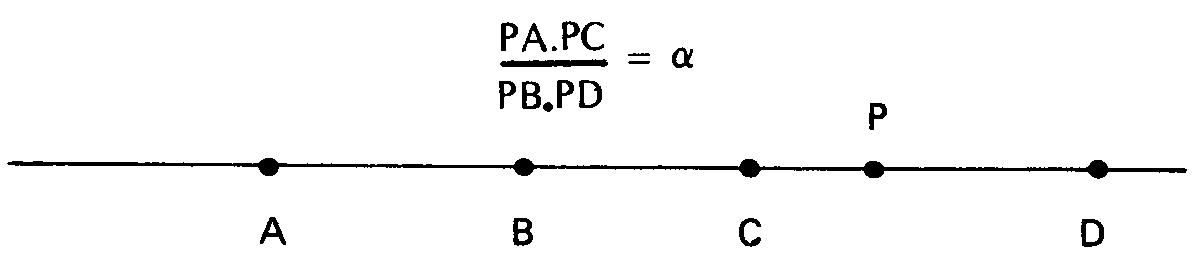La obra titulada Tangencias (Epajai)
se hizo especialmente famosa a lo largo de la historia por contener lo
que se vino a llamar el Problema de Apolonio. Dados tres elementos,
cada uno de los cuales puede ser un punto, una recta o una circunferencia,
se pide hallar una circunferencia que sea tangente a ellos (pase por ellos
en el caso de puntos). El caso más complicado, dadas tres circunferencias
hallar otra tangente a las tres, es el mencionado problema de Apolonio.
No conociéndose exactamente la solución de Apolonio, esta
cuestión interesó vivamente a muchos matemáticos famosos,
entre ellos Vieta, Descartes, Newton, Euler, Poncelet,...
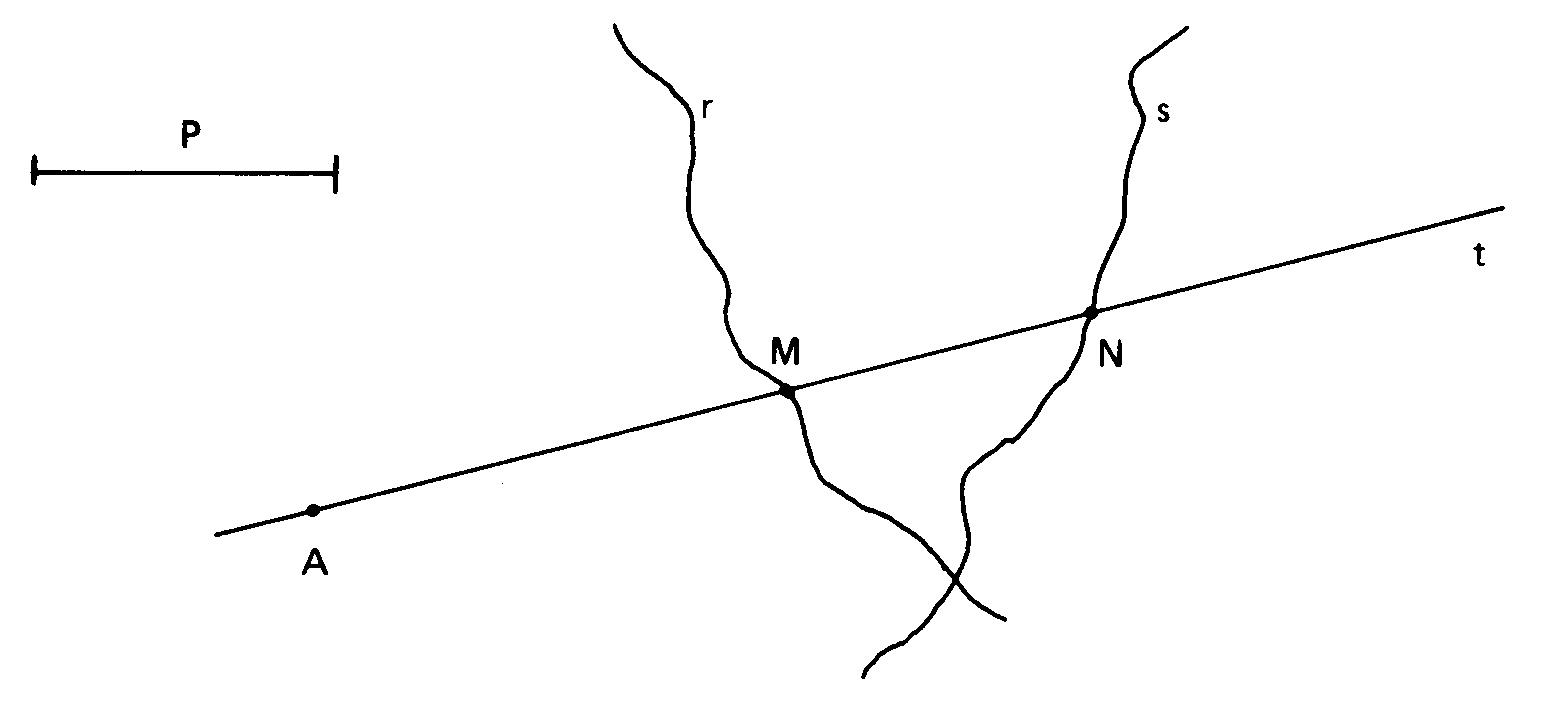
El problema tratado en la obra sobre
Inclinaciones (ueuseis) se puede proponer
en general como sigue: Dado un punto A, dos curvas r y s, y la longitud
p, hallar una recta t que pase por A tal que MN=p
El tratado sobre Lugares planos
(topoi epipedoi) estudia condiciones que conducen
a rectas y círculos como lugares geométricos.
De estos tratados se conocen algunas
referencias sobre el contenido a través de las noticias que proporciona
Pappus (siglo IV d.de C.), quien debió de tener ante sus ojos las
obras de Apolonio o al menos algún catálogo más extenso.
Hay aún otras obras que menciona cuyo contenido es más oscuro.
Una especie de Arenario, al estilo del de Arquímedes con
técnicas para manejar números grandes. Un tratado Sobre
la hélice. Otro Sobre el dodecaedro y el icosaedro, en
el que aparece la igualdad de las apotemas de los dos poliedros regulares
inscritos en la misma esfera, lo que conduce de modo directo a una fácil
comparación de volúmenes (mayor para el dodecaedro, contra
lo que una primera intuición podría sospechar). Pappus menciona
también un Tratado general (kaqolou pragmareia)
en el que podría haber observaciones sistemáticas de tipo
axiomático relativas a los fundamentos de la geometría. Existe
también una oscura alusión a un tratado Sobre los irracionales
desordenados (peri twu atak twu alogwu)
que tal vez podría consistir en consideraciones que extendían,
no se sabe bien en qué dirección, el contenido del libro
X de los Elementos de Euclides. Pappus cita también un trabajo sobre
Cálculo rápido (wkutokiou)
que debía de referirse al cálculo aproximado de p.
También se nombran en el cattálogo de Pappus dos trabajos
de óptica, Sobre el espejo cáustico (peri
toupureiou) y A los catrópticos (pros
tous katroptkous)
en los que sin duda los conocimientos geométricos de Apolonio se
ponían en acción con gran ventaja.
